Комплексные числа.
1.1.Найти действительную и мнимую части комплексного числа z.
1.  ;
| 2.  ;
|
3.  ;
| 4.  ;
|
5.  ;
| 6.  ;
|
1.2.К данному комплексному числу найти число обратное, противоположное и сопряженное. Данное число и все полученные числа записать в алгебраической и показательной форме. Изобразить их на комплексной плоскости.
1.  ;
| 2.  ;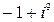
|
3.  ;
| 4.  ;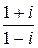
|
5.  ;
| 6.  ;
|
1.3.Найти все значения корней n-степени из комплексного числа а и построить их на комплексной плоскости.
1.  ;
| 2.  ;
|
3.  ;
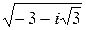| 4.  ;
|
5.  ;
| 6.  ;
|
1.4.Доказать тождество или неравенство.
1.  ;
| 2.  ;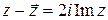
|
3.  ;
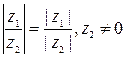| 4.  ;
|
2.1.Выяснить геометрический смысл указанных соотношений.
1.  ;
| 2.  ;
|
3.  ;
| 4.  ;
|
5.  ;
| 6.  ;
|
2.2.Найти на сфере Римана образы: а) точки и б) области, определяемой неравенствами.
1.  ;
| 2.  ;
|
3.  ;
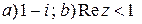| 4.  ;
|
5.  ;
| 6.  ;
|
4.2. Является ли функция w=f(z)=f(x+iy) дифференцируемой в смысле R2 по переменным x, y, и дифференцируемой в смысле C по переменной z? Опишите области дифференцируемости.
1. f(z) =  .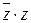
| 2. f(z) = sinx+ icosy |
| 3. f(z) = ex(sinx+icosy). | 4. f(z) == ex(siny+icosy). |
| 5. f(z)= ex(siny+icosy). | 6. f(z)= sin(|z|). |
4.4. Восстановить аналитическую в окрестности точки z0 функцию f(z). по по ее модулю или аргументу.
| 1.arg(f(z))=y. | 2.  .
|
3.  .
| 4.  .
|
5.  .
| 6.  .
|
5. Задания по плоскому комплексному потенциалу.
5.1. Плоское электростатическое поле имеет силовые линии x2 – y2 = c – const и напряженность E в точке (0,0) равна –3i. Найти эквипотенциальные линии поля и его комплексный потенциал.
5.2. Может ли функция u(z)=u(x+iy) = ln(x2 +y2) – x2 +y2 быть силовой или потенциальной функцией некоторого плоскопараллельного поля с комплексным потенциалом?
5.3. Выяснить характер электростатического поля (найти эквипотенциальные и силовые линии поля), соответствующего комплексному потенциалу f(z)=i/z.
5.4. Плоское электростатическое поле имеет силовые линии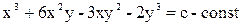 
и напряженность E в точке (0,0) равна – 0. Найти эквипотенциальные линии поля и его комплексный потенциал.
5.5. Может ли функция u(z)=u(x+iy) =2ln|z|+3 быть потенциальной функцией некоторого плоскопараллельного поля с комплексным потенциалом?
5.6. Плоское электростатическое поле имеет силовые линии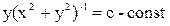 
и напряженность E в точке (2,0) равна – 0. Найти эквипотенциальные линии поля и его комплексный потенциал.
5.7. Может ли функция u(z)=u(x+iy) =|z|2+3|z|4 быть силовой или потенциальной функцией некоторого плоскопараллельного поля с комплексным потенциалом?
5.8. Выяснить характер электростатического поля, соответствующего комплексному потенциалу f(z)=2/z.
5.9. По заданному комплексному потенциалу плоского теплового поля w=z2 +4z +4 найти и изобразить изотермы, линии теплового потока и определить скорость потока v.
5.10. Найти поле скоростей движения несжимаемой жидкости, линии тока и эквипотенциальные линии, зная комплексный потенциал w=e2z.
5.11. Плоское электростатическое поле имеет силовые линии 
и напряженность E в точке (0,0) равна – 0. Найти эквипотенциальные линии поля и его комплексный потенциал.
5.12. Может ли функция u(z)=u(x+iy) =2argz2+3 быть потенциальной функцией некоторого плоскопараллельного поля с комплексным потенциалом?
5.13. По заданному комплексному потенциалу плоского теплового поля w=9+6z+z2 найти и изобразить изотермы, линии теплового потока и определить скорость потока v.
5.14. Найти поле скоростей движения несжимаемой жидкости, линии тока и эквипотенциальные линии, зная комплексный потенциал w=ilnz +3.
5.15. Плоское электростатическое поле имеет силовые линии 
и напряженность E в точке (1,0) равна 1. Найти эквипотенциальные линии поля и его комплексный потенциал.
5.16. Может ли функция 
, (a,b – const) быть силовой или потенциальной функцией некоторого плоскопараллельного поля с комплексным потенциалом?
5.17. Выяснить характер электростатического поля, соответствующего комплексному потенциалу f(z)=1/(z-2).
5.18. Найти поле скоростей движения несжимаемой жидкости, линии тока и эквипотенциальные линии, зная комплексный потенциал w=(3i+1)(z-1)2+3.
5.19. Плоское электростатическое поле имеет силовые линии 
и напряженность E в точке (0,0) равна 1. Найти эквипотенциальные линии поля и его комплексный потенциал.
5.20. По заданному комплексному потенциалу плоского теплового поля w=2z+z2 найти и изобразить изотермы, линии теплового потока и определить скорость потока v.
5.21. Найти поле скоростей движения несжимаемой жидкости, линии тока и эквипотенциальные линии, зная комплексный потенциал 
.
5.22. По заданному комплексному потенциалу плоского теплового поля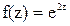 
найти изотермы, линии теплового потока и определить скорость потока v.
5.23. Выяснить характер электростатического поля, соответствующего комплексному потенциалу 
.
5.24. Может ли функция 
, (a,b – const) быть силовой или потенциальной функцией некоторого плоскопараллельного поля с комплексным потенциалом?
Вычислить
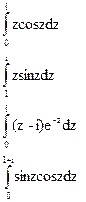
Найти вычеты
Вопросы для самоподготовки
1. Комплексные числа и действия над ними. Поле комплексных чисел. Модуль и аргумент комплексного числа, сопряженное число. Алгебраическая, тригонометрическая и показательная форма записи комплексного числа.
2. Топология комплексной плоскости. Окрестность точки. Проколотая окрестность точки. Открытое и замкнутое множество на комплексной плоскости. Бесконечно удаленная точка. Сфера Римана. Стереографическая проекция.
3. Кривые на комплексной плоскости. Путь, замкнутый путь, простой путь, эквивалентные пути. Жорданов, гладкий, и кусочно гладкий путь.
4. Связность и линейная связность. Связная компонента множества. Область. Граница области. Односвязные и многосвязные области. Множество компактно принадлежащее области. Расстояние между множествами. Расстояние между точками по области.
5. Функции комплексного переменного (ФКП) и действия над ними. Предел функции в точке. Функция непрерывная в точке. Функция непрерывная в области. Функция непрерывная вплоть до границы. Элементарные ФКП.
6. Дифференцируемость ФКП. R – дифференцируемость и C– дифференцируемость ФКП в точке. Условия Коши-Римана. Производная по направлению. Производная функции в точке. Функция голоморфная в точке и области. Функция голоморфная на произвольном множестве. Голоморфность в ФКП в бесконечно удаленной точке.
7. Аналитические и гармонические функции. Сопряженные гармонические функции. Восстановление голоморфной функции по ее вещественной или мнимой части.
8. Геометрический смысл производной. Однолистность ФКП. Угол поворота кривой в точке. Линейное растяжение кривой в точке. Касательное отображение. Якобиан отображения. Отображение конформное в точке. Связь между понятиями дифференцируемости и конформности в точке и в области.
9. Комплексный потенциал векторного поля. Применение ФКП в гидродинамике, электростатике.
10. Конформные отображения. Локальные свойства отображений голоморфными функциями. Однолистные функции, принцип сохранения области.
11. Отображения, задаваемые линейной, дробно-линейной, степенной и показательной функциями, функцией Жуковского, другими элементарными функциями.
12. Общие принципы конформных отображений. Теорема Римана.
Список литературы
1..Ю.В. Сидоров, М.В. Федорюк, М.И. Шабунин. Лекции по теории функций комплексного переменного. М.Наука, 1974.
2. Волковысский Л.И., Лунц Г.Л., Араманович И.Г. Сборник задач по теории функций комплексного переменного М.Наука, 1975.
3. Лаврентьев М.А. Методы теории функций комплексного переменного/М.А.Лаврентьев,Б.В.Шабат.-6-е изд., стереотип.-М.:Лань,2002.-688с.
4. Лунц Г.Л. Функции комплексного переменного с элементами операционного исчисления/Г. Л. Лунц, Л. Э. Эльсгольц.-СПб.:Лань,2002.-304с.
5. Пантелеев А.В. Теория функций комплексного переменного и операционное исчисление в примерах и задачах:Учеб. пособие/А.В.Пантелеев, А.С.Якимова.-М.:Высш. школа, 2001.-445с.:ил.
6. А.Г. Свешников, А.Н. Тихонов. Теория функций комплексной переменной.
7. И.И. Привалов. Введение в теорию функций комплексного переменного
8..М.А. Евграфов. Аналитические функции.
9..Т.А.Леонтьева, В.С.Панферов, В.С. Серов. Задачи по теории функций комплексного переменного. М:Мир, 2005. –360 с.
