Определение 7. Говорят, что на множестве М из С задана функция f, если задан закон, по которому каждой точке z из М ставиться в соответствие комплексное число w (конечное или бесконечное). Обозначается
или 
.
Хотя мы пишем 
– функция вроде бы зависит только от z, мы предполагаем, что она может зависеть и от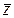 
. Этим и объясняется дальнейшее продолжение записи
,
т.е. задание комплекснозначной функции равносильно заданию двух вещественных функций. Функцию 
называют вещественной частью и 
– называют мнимой частью функции f.
Если еще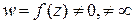 
, то, полагая 
, можно записать эту функцию в виде двух соотношений (полярное задание)
.
Т.к. аргумент не определен в точках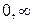 
, в этом случае нам нужно исключить его из рассмотрения. Последнее задание не пользуется такой популярностью, как задание функции с помощью двух вещественных функций и .
Согласно определению 7 всякая функция однозначна (т.е. каждому z соответствует только одно w). Если мы будем рассматривать многозначные функции, то будем оговаривать это особо. Если функция преобразует различные точки в различные, то она называется взаимно однозначной или однолистной. Рассмотрим примеры некоторых элементарных функций.
w = z2, z Î C, однозначная функция, корректно определена, т.к введено произведение комплексных чисел.
, z Î C, однозначная функция, определена на основании формулы Эйлера и вещественной функции 
.
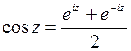z Î C, однозначная функция, определяется опираясь на функцию 
.
z Î C, однозначная функция определяется опираясь на функцию .
w = 
является многозначной функцией, определяется, как функция обратная 
.
w = ln z = ln r + i j, j = arg z Î (-p,p], D = C \{0}, однозначная функция.
w = Arg z = arg z + 2pk, (k -любой целое) многозначная функция.
w = Ln z = ln r + i j + 2pik, j = arg z Î (-p,p], k -целое, D = C \0, многозначная функция, определяется как обратная функция к .
w = zb = eb Ln z может быть для некоторых b многозначной (для натуральных b определение согласуется с операцией возведения в степень путём перемножения).
Если функция f(z) однозначная, то можно обычным образом определить обратную функцию 
. Для этого обозначим через D область определения функции f(z), аобласть ее значений через D. Обратная функция f -1 будет определена на D и каждому значению w из D будет сопоставлять все те значения z из D для которых f(z) = w. Обратная функция не обязана быть однозначной.
Если f и однозначные, то отображение z ® w = f(z) будет однолистным (отображение взаимно однозначное).
Пример: функция w=z2 отображает однолистно область D={|z|<1,0<arg z < p} верхний полукруг на круг с разрезом по положительной вещественной оси.
Рис.9
При исследовании многозначных функций выделяют однозначные ветви. Например, рассмотрим функцию 
, в качестве области определения D возьмём всю комплексную плоскость с вырезом по положительной части действительной оси, xÎ[0,¥). В этой области рассмотрим функции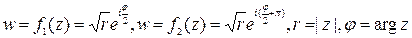 
(здесь главное значение аргумента комплексного числа считается выбираемым в диапазоне 0 £ arg z < 2p). Эти функции представляют собой однозначные ветви исходной функции в области D. Первая отображает область D на верхнюю полуплоскость, вторая функция отображает область D на нижнюю полуплоскость. Однозначные ветви можно выделять по разному.
Можно определить элементарные функции используя их вещественные разложением в ряды Тейлора.
;
;
;
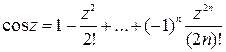
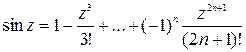
Пример 3.1. Представить в алгебраической форме 
.
Решение. Найдем модуль и аргумент числа стоящего под логарифмом
.
Пользуясь формулой главного значения логарифма
.
Пример 3.2. а) Найти образ линии Rez = 1 при отображении w = f(z) = Rez/z.
б) Найти образ полуполоса 
, 
, при отображении 
Решение. а).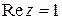 
– это все числа вида 
, где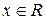 
.
, 
. Данная кривая и будет являться образом линии 
. Это будет окружность с центром в точке (0.5, 0) радиуса 0.5.
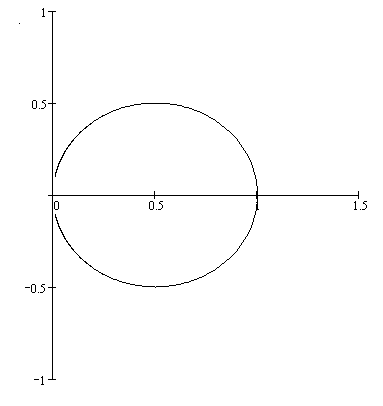
Рис.9
б). 
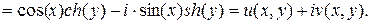
Рассмотрим, как отображаются линии, являющиеся границами заданной области.
1) отрезок у=0, 0<x<p отображается в w=cos(x). Т.е. w=u, где u 
(-1, 1).
2) Луч x=0, - 
<y<0 отображается в w=cos(iy)=ch(y), т.е. w=u (1, 
).
3) Луч x=p, - <y<0 отображается в w=-cos(iy)=-ch(y), т.е. w=u (, 1).
Таким образом, граница данной фигуры переходит во все точки действительной оси u (в комплексной плоскости с координатами u, v) кроме точек –1 и 1. Значит, наша фигура отобразится в верхнюю или нижнюю полуплоскость комплексной плоскости w. Узнаем, в какую именно.
.
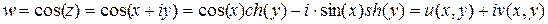Рассмотрим, какие значения принимает 
. Т.к. 0<x<p, то sin(x)>0. y<0, следовательно, sh(y)<0. Таким образом, 
>0. То есть данная фигура отображается на всю верхнюю полуплоскость комплексной плоскости w.
