Отсюда получаем формулу:
,
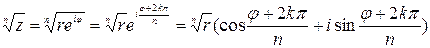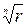– берется арифметический, k придаются значения 0, 1, …, n-1. При других целых значениях k найденные значения корня повторяются. Геометрически эти n значений корня изобразятся вершинами правильного n-угольника, вписанного в окружность, в центром в нулевой точке, радиусом 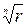, вершины которого имеют полярные координаты
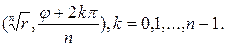
Пример 1.3. Найти все значения корней 8-степени из комплексного числа 
и построить их на комплексной плоскости.
Решение. Представим комплексное число в показательной форме
,
следовательно,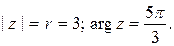 
Всего будет восемь корней, общая формула для корня восьмой степени имеет вид
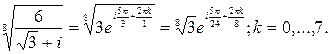
Все корни расположены на окружности радиуса с центром в нуле, и делят эту окружность на восемь равных частей.
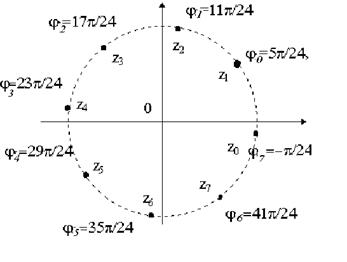
Рис.3
Т.е. все корни имеют одинаковый модуль равный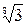 
и получаются из одного из корней последовательным поворотом на кратный 
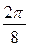угол.
Области и кривые на комплексной плоскости.
По аналогии с вещественной плоскостью (вещественным пространством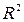 
) строится топология комплексной плоскости C. Задать топологию – значит определить какие множества будут называться открытыми и какие замкнытуми.
Самое простое открытое множество – это открытый круг. С помощью модуля комплексного числа его задать особенно просто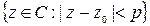 
– это все комплексные числа из круга с центром в точке 
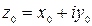, радиуса p, Причем, т.к. неравенство в задании круга строгое, то точки лежащие на окружности в этот круг не включаются. Т.е. это круг без граничной окружности, поэтому его целесообразно назвать открытым. Теперь можно дать определение открытого и замкнутого множеств.
Определение 4. Множество М из С называется открытым, если любая точка из М принадлежит М вместе с открытым кругом не нулевого радиуса. Множество М из С называется замкнутым, если оно является дополнением некоторого открытого множества.
Обычно, определение замкнутых множеств дают, как множества содержащие все свои предельные точки или множества, содержащие свою границу. Ясно, что открытые и замкнутые множества являются дополнениями друг друга. Все эти определения замкнутых множеств для нашего случая эквивалентны. К сожалению, существуют множества, которые не открыты и не замкнуты. Таким будет открытый круг, если к нему добавить любую точку на плоскости не попадающую в данный круг.
Для того, чтобы дать определение области, нам потребуется понятие непрерывной кривой.
Определение 5. Множество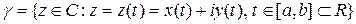 
называется непрерывным образом отрезка 
или непрерывной кривой, если вещественные функции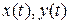 
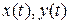непрерывны на отрезке . Если функции непрерывно дифференцируемы на отрезке , то g называется главдкой кривой. При этом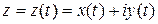 
называется параметрическим представлением кривой g.
Для каждой непрерывной кривой g фиксируется одно из двух взаимно противоположных направлений движения подвижной точки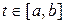 
, соответствующее возрастанию или убыванию параметра. В первом случае 
есть начало,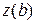 
– конец кривой, а во втором случае эти точки меняются местами. Кривая, начальная и конечная точки которой совпадают, называется замкнутой. Если одна и та же точка кривой соответствует двум или более различным значениям параметра, из которых по крайней мере одно отлично от а и b, то такая точка называется кратной. Непрервыная кривая, не имеющая кратных точек, называется жордановой или простой. Иными словами, если отображение, определяющее кривую взаимнооднозначно, то кривая жорданова или простая. Если начальная и конечная точки кривой совпадают, то жорданова кривая называется замкнутой. Если две любые точки множества М можно соеденить непрерывной кривой, то это множество называется линейно связным. Для открытых множеств понятия линейной связности и просто связности совпадают.
