¬их≥дн≥ дан≥
–озвТ€занн€ поставленоњ задач≥ виконуЇтьс€ на приклад≥ п≥дсистеми розформуванн€, принципова схема €коњ наведена на рис. 1.
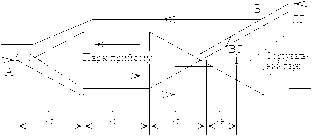
–ис. 1. —хема п≥дсистеми розформуванн€.
ƒл€ виконанн€ розрахунк≥в студенту видаЇтьс€ ≥ндив≥дуальне завданн€, приклад €кого приведено нижче.
1. —татистичний р€д ≥нтервал≥в прибутт€ поњзд≥в у розформуванн€.
| ≤нтервали, хвилин | 0..10 | 10..20 | 20..30 | 30..40 | 40..50 | 50..60 | 60..70 | 70..80 |
| ≥льк≥сть спостережень | - |
2. —татистичний р€д к≥лькост≥ вагон≥в у состав≥.
| ≥льк≥сть вагон≥в | 35..37 | 38..40 | 41..43 | 44..46 | 47..49 | 50..52 | 53..55 | 56..58 |
| ≥льк≥сть спостережень | - |
3. ѕараметри тривалост≥ обслуговуванн€ одного вагона:
- математичне оч≥куванн€ ћ [τоб] = 1,00 хв/вагон,
- коеф≥ц≥Їнт вар≥ац≥њ υ[τоб] = 0,25.
4. ѕараметри тривалост≥ розпуску з г≥рки одного вагона:
- математичне оч≥куванн€ ћ [τр] = 0,20 хв/вагон;
- коеф≥ц≥Їнт вар≥ац≥њ υ[τр] = 0,30.
5. оеф≥ц≥Їнт вар≥ац≥њ тривалост≥ г≥рочного технолог≥чного ≥нтервалу υг=0,40.
6. ѕараметри п≥дсистеми розформуванн€:
- довжина горловин парку прийому l г = 250 м;
- довжина кол≥й парку прийому l к = 850 м;
- довжина кол≥њ насуву l н = 100 м.
–озрахунок параметр≥в ≥ визначенн€ характеру вх≥дного потоку поњзд≥в у п≥дсистему розформуванн€ сортувальноњ станц≥њ
ƒл€ досл≥дженн€ процес≥в, €к≥ в≥дбуваютьс€ на транспортних обТЇктах, потр≥бн≥ дан≥ про вх≥дний пот≥к вимог, €к≥ можуть бути подан≥ параметрами розпод≥лу ≥нтервал≥в прибутт€ поњзд≥в (у подальшому ≥нтервал≥в). “акими параметрами €вл€ютьс€: математичне оч≥куванн€ ≥нтервал≥в (ћ [ I ]), дисперс≥€ (D [ I ]), середнЇ квадратичне в≥дхиленн€ (σ[ I ]), коеф≥ц≥Їнт вар≥ац≥њ (υ[ I ]) та ≥нтенсивн≥сть вх≥дного потоку (λ). ” контрольн≥й робот≥ ц≥ параметри визначаютьс€ на основ≥ заданого статистичного р€ду розпод≥лу ≥нтервал≥в (п.1 завданн€), дл€ чого складаЇтьс€ розрахункова таблиц€ (табл. 1).
” табл. 1 к≥льк≥сть розр€д≥в (колонка 1), д≥апазон ≥нтервал≥в (колонка 2), к≥льк≥сть спостережень (колонка 4) в≥дпов≥дають заданому розпод≥лу ≥нтервал≥в (п.1 завданн€). ƒл€ кожного розр€ду визначаЇтьс€ середнЇ значенн€ ≥нтервалу у розр€д≥ (колонка 3):
Ī j = (I min + I max),
де I min, I max Ц в≥дпов≥дно найменше ≥ найб≥льше значенн€ ≥нтервал≥в у розр€д≥ (колонка 2).
“аблиц€ 1
| єє розр€д≥в | ƒ≥апазон ≥нтервал≥в | —ередина розр€ду Ī j, хв. | ≥льк≥сть спостережень, K j | B j | Ī j B j | Ī j2 B j |
| 0..10 | 0,126 | 0,630 | 3,150 | |||
| 10..20 | 0,211 | 3,165 | 47,475 | |||
| 20..30 | 0,253 | 6,325 | 158,125 | |||
| 30..40 | 0,179 | 6,265 | 219,275 | |||
| 40..50 | 0,105 | 4,725 | 212,625 | |||
| 50..60 | 0,074 | 4,070 | 223,850 | |||
| 60..70 | 0,053 | 3,445 | 223,925 | |||
| ¬сього | n = 95 | 1.001 | 28.625 | 1088.425 |
≥льк≥сть спостережень ( j) у розр€д≥ (колонка 4) за зм≥стом €вл€Ї собою к≥льк≥сть ≥нтервал≥в, €к≥ мають величину в≥д I min до I max. « використанн€м к≥лькост≥ спостережень у кожному розр€д≥ визначаЇтьс€ статистична ймов≥рн≥сть або част≥сть влучанн€ випадковоњ величини ≥нтервалу до в≥дпов≥дного розр€ду
|
|
|
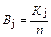 ,
,
де n Ц загальна к≥льк≥сть спостережень, у приклад≥ n = 95.
ќтриман≥ значенн€ B j навод€тьс€ у в≥дпов≥дн≥й граф≥ табл. 1 ≥ повинн≥ в≥дпов≥дати умов≥ Σ B j = 1,0. «а зм≥стом окрема величина B j €вл€Ї собою частку випадк≥в або статистичну ймов≥рн≥сть того, що випадкова величина матиме значенн€ у межах I min(j) ≤ I < I max(j).
« використанн€м B j дл€ кожного розр€ду розраховують величини Ī j B j та Ī j2 B j, €к≥ внос€ть до в≥дпов≥дних граф табл. 1, ≥ визначають њх суми Σ IB та Σ I 2 B.
«а даними табл. 1 визначаютьс€ параметри розпод≥ленн€ ≥нтервал≥в.
ћатематичне оч≥куванн€ за зм≥стом €вл€Ї собою середньозважену величину ≥нтервалу, в≥дносно €кого розс≥€н≥ випадков≥ значенн€ ≥нтервал≥в, ≥ розраховуЇтьс€ €к
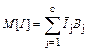 , (1)
, (1)
де c Ц к≥льк≥сть розр€д≥в статистичного р€ду.
ƒл€ умов прикладу (див. табл. 1) ћ [ ≤ ] = 28,625 ≈ 28,6 хв.
≤нтенсивн≥сть вх≥дного потоку, тобто середн€ к≥льк≥сть поњзд≥в, що прибувають за одиницю часу
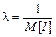 . (2)
. (2)
ƒл€ умов прикладу маЇмо 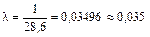 поњзд≥в/хв.
поњзд≥в/хв.
ћатематичне оч≥куванн€ квадрату ≥нтервалу визначаЇтьс€ €к
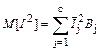 , (3)
, (3)
≥ становить (див. табл. 1) M [ I 2] = 1088,425 хв 2.
ƒисперс≥€ характеризуЇ коливанн€ випадковоњ величини в≥дносно њњ математичного оч≥куванн€, €вл€Ї собою середньозважену величину квадрата в≥дхиленн€ випадкових значень ≥нтервал≥в в≥д ћ [ ≤ ], визначаЇтьс€ €к
D [ ≤ ] = M [ I 2] Ц (M [ I ])2, (4)
≥ дл€ умов прикладу становить D [ ≤ ] = 1088,425 Ц 28,62 = 270,465 хв 2.
—ередньоквадратичне в≥дхиленн€ ≥нтервал≥в прибутт€ визначаЇтьс€ €к
σ[ I ] = 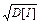 , (5)
, (5)
≥ становить у приклад≥ 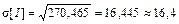 хв.
хв.
оеф≥ц≥Їнт вар≥ац≥њ ≥нтервал≥в прибутт€ (вх≥дного потоку) - в≥дносна м≥ра розс≥ву випадковоњ величини в≥д математичного оч≥куванн€
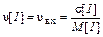 , (5)
, (5)
становить у приклад≥ 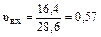 .
.
“аким чином, вх≥дний пот≥к поњзд≥в Ї випадковим ≥ за характером не найпрост≥ший, оск≥льки υвх= 0,57. ” випадку, коли υвх= 1, пот≥к Ї найпрост≥шим.






