Цель работы: познакомиться с применением закона сохранения энергии к процессу скатывания тележки с горки, определить зависимость скорости скатывания от массы тележки.
Оборудование: четырехколесная тележка как модель вагона, набор грузов, секундомер, модель сортировочной горки.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Сортировочная горка – это устройство, позволяющее благодаря наклону путей скатывать вагоны под действием силы тяжести на разветвляющие пути для формирования и расформирования составов.
Для определения скорости скатывания вагона с горки высотой Н применим закон сохранения энергии. Попытка применения закона сохранения механической энергии в виде: потенциальная энергия вагона на вершине горки по мере скатывания переходит в кинетическую энергию поступательного движения вагона, 
, приводит к результату: 
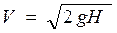. По этой формуле скорость скатывания не зависит от массы вагона. На самом деле груженые вагоны скатываются быстрее порожних вагонов. Возможно потому, что колеса вагона не только движутся поступательно вместе с вагоном, но еще и вращаются. Соответственно к кинетической энергии поступательного движения вагона следует еще добавить кинетическую энергию вращательного движения колесных пар.
Катящееся колесо совершает так называемое плоское движение, при котором траектории всех точек колеса лежат в параллельных плоскостях. Плоское движение можно представить двумя способами: или как сумму вращательного движения относительно оси, проходящей через центр масс, и поступательного движения со скоростью центра масс, или как вращение колеса вокруг мгновенной оси вращения. Мгновенная ось – это линия, точки которой в данное мгновение покоятся. Ее положение со временем изменяется. Например, для колес вагона мгновенная ось проходит через точки контакта колесной пары с рельсами и со временем эта ось перемещается.
В первом способе представления качения выразим кинетическую энергию всех катящихся колес вагона как сумму кинетических энергий поступательного движения со скоростью вагона и вращательного движения колес относительно осей колесных пар:
. (1)
Здесь J – момент инерции колесных пар относительно их осей. В уравнении (1) произведена замена 
, так как если нет проскальзывания, то скорости поступательного и вращательного движений точек контакта с рельсом равны и противоположны (рис. 1).
Пренебрежем потерями механической энергии на трение, полагая, что сила трения качения незначительна по сравнению с компонентой силы тяжести 
(рис. 2). Тогда для процесса скатывания вагона выполняется закон сохранения механической энергии:потенциальнаяэнергия на вершине горки по мере скатывания переходит в кинетическую энергию поступательного движения вагона вместе с колесами с общей массой m и в кинетическую энергию вращательного движения колес относительно их осей:
. (2)
Выразим высоту горки через ее длину 
. Скорость вагона у основания горки будет
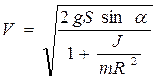. (3)
Как видно по знаменателю формулы (3), учет энергии вращения колес приводит к уменьшению скорости скатывания вагона. Момент инерции всех колесных пар вагона J является величиной постоянной. Поэтому, чем больше масса груза в вагоне, тем меньше роль инертности вращения колес, тем меньше коэффициент инертности 
, тем больше скорость скатывания. Коэффициент инертности имеет значение 1,05 для груженых вагонов, для порожних вагонов больше – 1.10.
 |
Реально уклон сортировочной горки не постоянен. В начале уклон делают сравнительно крутым, а потом более пологим. Соответственно скорость сначала быстро возрастает, и вагон скатывается за более короткое время. Это увеличивает производительность горки. Но конечная скорость по закону сохранения энергии от профиля горки не зависит.
Таким образом, из уравнения (3) следует, что квадрат скорости скатывания должен быть пропорционален величине обратной коэффициенту инертности: 
.
Лабораторная установкадля определения зависимости скорости скатывания тележки от массы представляет собой наклонный желоб с металлическими уголками, играющих роль рельсов. Модель вагона – это четырехколесная тележка со специально сравнительно массивными колесами. Изменение массы тележки производится дополнительными грузами. Скорость в конце спуска определяется по времени скатывания, измеряемого секундомером. Полагая движение тележки равноускоренным: 
, отсюда получим
. (4)
Включение и выключение секундомера производится выключателями в начале и конце спуска.
ВЫПОЛНЕНИЕ РАБОТЫ
1. Определить массу порожней тележки взвешиванием. Измерить радиус колес. Определить длину и установленный уклон горки. Записать результаты в табл. 1.
2. Включить блок питания установки в сеть 220 В. Произвести скатывание тележки. Поставить ее на рельсы у верхнего края, прижав к верхнему выключателю для разрыва цепи секундомера. Нижний выключатель включить. Нажать кнопку Сброс секундомера и отпустить тележку. Цепь замкнется верхним выключателем, и секундомер начнет счет. После удара тележки о нижний выключатель цепь разорвется, секундомер покажет время скатывания. Опыт произвести три – четыре раза. Повторяющийся результат записать в табл. 2.
Таблица 1 Таблица 2
| Масса колес, кг | 0,246 |
| Масса тележки, кг | |
| Радиус колес, м | |
| Уклон, sin α. | |
| Длина горки S, м | |
|
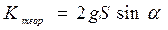
| m, кг | t, с | V, м/с | V 2 (м/с)2 | 1 /γ |
3. Повторить измерения времени скатывания, нагружая тележку грузами известной массы. Опыты провести не менее 6 раз. Результаты измерений времен скатывания и суммарную массу тележки с грузами записать в табл. 2.
Выключить блок питания.
4. Произвести расчеты в системе СИ. Определить скорости скатывания тележки по формуле (4) и значения квадрата скорости в каждом опыте.
5. Определить обратное значение коэффициента инертности тележки. Так как колеса являются дисками c моментом инерции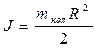 
, то 
. Результаты расчетов записать в табл. 2.
5. Построить график зависимости квадрата скорости от коэффициента 
. Размер графика не менее половины страницы. Так как зависимость является линейной, то около точек провести прямую линию.
6. На линии как на гипотенузе построить прямоугольный треугольник. По координатам вершин определить угловой коэффициент линии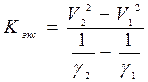 
. Определить теоретическое значение углового коэффициента 
.
7. Сравнить экспериментальное и теоретическое значение углового коэффициента.
Сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Объяснить назначение сортировочной горки на станции.
2. Объяснить, как зависит скорость скатывания вагона с горки, если не учитывать влияние инертности вращения колес.
3. Записать формулу кинетической энергии колеса, которое катится по рельсу.
4. Вывести формулу работы силы трения качения при скатывании вагона с горки.
5. Записать и объяснить уравнение закона сохранения полной энергии вагона при скатывании с горки.
6. Объяснить, при каких условиях результат работы подтверждает теоретическую зависимость скорости скатывания вагона от его массы.
Работа 19
