x = A 1sin(w 1 t + j 1), y = A 2sin (w 2 t + j 2). (1)
В математике это задание функции y (x) в параметрической форме. Здесь параметром является время. Зависимость y (x) является уравнением траектории. В общем случае траектория будет незамкнутой кривой, бесконечно заполняющей прямоугольник со сторонами 2 А 1 – 2 А 2. . Лишь в том случае, когда отношение частот равно отношению целых чисел, траектория движения замыкается и периодически повторяется. Такие траектории называются фигурами Лиссажу.
Пример 1.Пусть частоты колебаний равны, w 1 = w 2, разность фаз равна нулю: x = A 1sin(w t), y = A 2sin(w t). Чтобы найти уравнение траектории, то есть зависимость y(x), следует из уравнений исключить параметр – время t, каким-либо способом. В данном случае для этого достаточно поделить уравнения. В результате получим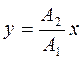 
. Это уравнение прямой линии, проходящей через начало координат из первого в третий квадрант (рис. 1, Δ φ = 0). Если разность фаз равна p радиан, то знак, например, для координаты y, меняется на отрицательный и траектория колебаний проходит из второго в четвертый квадрант.
Пример 2. Пусть частоты колебаний равны, разность фаз равна p /2. Уравнения (1) примут вид: x = A 1sin (w t), y = A 2cos(w t). Чтобы исключить время t, воспользуемся теоремой тригонометрии: сумма квадратов синуса и косинуса равна единице. Подставив функции синуса и косинуса из уравнений колебаний, получим 
. Это уравнение эллипса с полуосями А 1 и А 2. Движение по траектории начинается в точке C и происходит по часовой стрелке (рис. 1, Δ φ = π/2). Если амплитуды складываемых колебаний равны, то траектория будет окружностью радиуса, равного амплитудам.
Пример 3. Пусть частоты колебаний отличаются в два раза, начальные фазы равны нулю: x = A 1sin w t, y = A 2sin2 w t. Получим уравнение траектории, исключив время. Подставив функции синусов из уравнений колебаний в формулу тригонометрии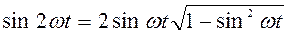 
, получим 
. Траектория похожа на цифру «восемь», (рис. 2 а). В начальный момент времени точка начинает движение из начала координат, двигаясь по часовой стрелке.
Пример 4. Пусть частоты колебаний отличаются в два раза, разность начальных фаз равна π/ 2: x = A 1sin w t, y = A 2cos2 w t. Подставив в формулу cos2 w t = 1–2sin2 w t функции синуса и косинуса, получим 
Это уравнение параболы, вершина которой смещена по оси Оy на + А 2, а ветви опущены вниз (рис.2 b). Движение начинается с вершины.
При движении точки по траектории она касается стенок прямоугольника 2 А 1 – 2 А 2. Отношение числа касаний вертикальных стенок к числу касаний горизонтальных стенок равно отношению частот колебаний по горизонтали и вертикали. Если разность начальных фаз равна нулю, то линия фигуры проходит через начало координат.
Фигуры Лиссажу используются при определении частот и начальных фаз неизвестных колебаний при сложении с колебаниями эталонного генератора.
В данной лабораторной работе изучение сложения взаимно перпендикулярных колебаний производится с помощью цифрового осциллографа. Осциллограф предназначен для исследования электрических сигналов путем визуального наблюдения на жидкокристаллическом дисплее и для измерения их амплитудных и временных параметров. Если на вертикальный и горизонтальный входы осциллографа подать от двух генераторов электрические гармонические колебания кратных частот, то на экране можно наблюдать фигуры Лиссажу (рис.3).
ВЫПОЛНЕНИЕ РАБОТЫ
1. Проверить подсоединение кабелей генераторов на вертикальный и горизонтальный входы осциллографа в соответствие с маркировкой. Включить в сеть 220 В генераторы и осциллограф. Нажать кнопки Сеть приборов.
2. На дисплеях генераторов будет указана исходные параметры: частота 1.00000 кГц и амплитуда сигнала 1,000 В. Амплитуда достаточна, а частоту следует уменьшить, иначе точки, которыми изображена фигура Лиссажу на экране, будут расположены редко. Для этого нажмите на панели функций кнопку частоты Freq, если она не светится. Будет мигать цифра активированного разряда частоты. Уменьшайте частоту поворотом ручки Регулятор примерно до ста герц. Кнопками под регулятором < или > можно активировать другие разряды.
 |
Аналогичные операции проведите со вторым генератором. Установите в первом опыте одинаковые частоты.
3. Если настройки осциллографа сохранились с предыдущего занятия, то на экране будет изображение фигуры Лиссажу в форме эллипса, который медленно поворачивается из-за изменения разности начальных фаз генераторов. Остановить можно, варьируя частоту одного из генераторов в последнем разряде. Но это не обязательно. Наоборот, увеличив разность частот, можно получить более быстрый поворот фигуры.
Если настройки не сохранились, то нажмите кнопку Displey. Внизу экрана появится окно диалога. Включите операцию сложения колебаний XY кнопкой H -3. На экране появится эллипс.
Зарисуйте в таблицу фигуры Лиссажу. Для определения разности фаз отключите сложение колебаний кнопкой H -3. Если красная и желтая синусоиды совпадают в начале координат, то разность фаз равна нулю. Если изображения смещены на четверть периода (одна переходит через нуль, а другая через максимум), то разность фазравна π/ 2.
| w 1 : w 2 | Разность фаз | |
| p/2 | ||
| 1:1 | ||
4. Не менее двух раз повторить обнаружение фигур Лиссажу при другом соотношении частот. Для этого медленно изменяйте частоту одного из генераторов. Как только осциллограмма стабилизируется, исследуйте её. Определите соотношение частот, зарисуйте фигуры при разности фаз 0, π/ 2.
Выключить приборы.
5. Сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Запишите уравнение гармонических колебаний. Дайте определение параметрам движения.
2. Дайте определение фигур Лиссажу, условия их образования. Как влияет на форму фигуры синхронное изменение частот и амплитуд сигналов генераторов?
3. Выведите уравнение траектории при сложении взаимно перпендикулярных колебаний одинаковой частоты.
4. Выведите уравнение траектории точки при сложении взаимно перпендикулярных колебаний, частоты которых отличаются в два раза.
5. Докажите, что через время, кратное периодам колебаний, движение точки повторяется (например, из начала координат).
6. Объясните применение фигур Лиссажу.
Работа 13
