Квадратные неравенства и их системы

Определение: Неравенства вида и , где х – переменная, а, b, с - действительные числа, причем а ¹ 0, называются квадратными неравенствами (неравенствами второй степени с одной переменной).

Пример:

1. 

х

-

+

+

Ответ:

1. 

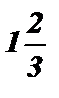
   х

   - 4,5

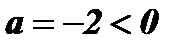, ветви параболы направлены вниз

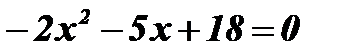
Ответ:x Î (- 4,5; 2)

Упражнения:

1. ;	2. ;	3. ;
4. ;	5. ;	6. ;
7. 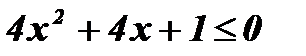;	8. ;
9.	10.	11.

Системы линейных уравнений с двумя переменными

8.3. Основные понятия

 

Определение: Линейным уравнением с двумя переменными называется уравнение вида , где x, y – переменные, a, b, c – некоторые числа.

 

Определение: Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное числовое равенство.

Пример:2x – y = 5 – линейное уравнение с двумя переменными x и y.

(0; –5); (2; –1); (5; 5) – решения линейного уравнения 2x – y = 5.

 

Вывод:

1. Линейное уравнение с двумя переменными имеет бесконечное множество решений.

2.

-1

- 5

х

у

Графиком линейного уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых являются решениями этого уравнения (графиком уравнения является прямая).

 

Пример: или

 

x
y	– 5	– 1

Определение: Система линейных уравнений с двумя переменными имеет вид

a₁, а₂ - коэффициенты при x,

b₁, b₂ - коэффициенты при y,

c₁ , c₂ - свободные члены.

Определение: Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное числовое равенство.

Определение: Решить систему уравнений – значит найти все ее решения или доказать, что их нет.

8.4. Решение систем линейных уравнений с двумя переменными графически, подстановкой, сложением

х

-3

у

-2

l1

l2

М

Графический способ

 

Пример:Решить графически систему уравнений:

1)

l ₁: l ₂:

x		- 2		x		- 3
y				y

Координаты любой точки прямой l₁ являются решениями уравнения 2x + 3y = 5.

Координаты любой точки прямой l₂ являются решениями уравнения 3x – y = – 9.

Координаты x = – 2, y = 3 точки М пересечения прямых l₁ и l₂ удовлетворяют обоим уравнениям системы, то есть являются решением системы.

Ответ:(- 2; 3) – единственное решение системы.

y

1

-1

0

x

l1(l2)

2)

y = ; y = y = – l₁

y = ; y = ; y = – l₂

Прямые l₁ и l₂ совпадают. Координаты любой точки прямой являются решениями обоих уравнений системы.

х
у	- 1

х

y

l1

l2

Ответ: Система имеет бесконечное множество решений .

3) Û

l₁: l₂:

х				х
у			у

Прямые l₁ и l₂ параллельны и не имеют общих точек.

Ответ:Система не имеет решений.

Способ подстановки

1) Выразить из какого-нибудь уравнения системы одну переменную через другую.

2) Подставить в другое уравнение системы вместо этой переменной полученное выражение.

3) Решить получившееся уравнение с одной переменной.

4) Найти соответствующее значение другой переменной.

Пример:Решить систему уравнений способом подстановки:

1) Û Û

 

2x + 9x + 27 = 5; 11 x = – 22; x = – 2;

y = 3× (– 2) + 9; y = 3.

Ответ:(–2; 3)

2) Û Û

; ; 15 = 15.

Ответ:Система имеет бесконечное множество решений

3) Û

 

6 4

Ответ: Система не имеет решений.

 

Способ сложения

1) Умножить почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными (равными).

2) Сложить (вычесть) почленно левые и правые части уравнений системы.

3) Решить получившееся уравнение с одной переменной.

4) Найти соответствующее значение второй переменной.

Пример: Решить систему уравнений способом сложения:

1) Û

 

11x = – 22; x = –2

3·(–2) – y = – 9; y = 9 – 6; y = 3

Ответ:(–2; 3)

2) Û Û

Ответ:Система имеет бесконечное множество решений .

3) Û 0

Ответ:Система не имеет решений.

 

Упражнения: Решить системы двух линейных уравнений с двумя переменными графически, подстановкой, сложением:

1.	2.
3.	4.
5.	6.
7.	8.

Контрольные вопросы по теме

" Функции, их свойства и графики. Степенная функция"

 

1. Дать определение постоянной, абсолютной постоянной величин.

2. Дать определение переменной величины.

3. Дать определение функции.

4. Дать определение области определения функции.

5. Дать определение множества значений функции.

6. Дать определение четной, нечетной функции.

7. Дать определение монотонной, возрастающей, убывающей функции.

8. Дать определение обратимой функции.

9. Дать определение промежутков знакопостоянства функции.

10. Дать определение нулей функции.

11. Дать определение ограниченной, ограниченной сверху, ограниченной снизу функции.

12. Дать определение графика функции.

13. Степенная функция, ее свойства и графики.

14. Линейная функция, ее свойства и графики.

15. Квадратичная функция, ее свойства и графики.

16. Линейное уравнение с одной переменной (определение, решение).

17. Квадратное уравнение (определение, решение).

18. Разложение квадратного трехчлена на множители (формула).

19. Биквадратное уравнение (определение, решение).

20. Иррациональное уравнение (определение, решение).

21. Уравнения, содержащие переменную под знаком модуля (способы решения).

22. Квадратное неравенство (определение, решение).

23. Системы линейных уравнений с двумя переменными (способы решения).