Определение: Числовые промежутки, на которых функция сохраняет свой знак, то есть остается положительной или отрицательной, называются промежутками знакопостоянства функции.
Вывод:
1. Если на некотором промежутке график функции расположен выше оси абсцисс, то функция на этом промежутке принимает положительные значения.
2. Если на некотором промежутке график функции расположен ниже оси абсцисс, то функция на этом промежутке принимает отрицательные значения.
Определение: Значения аргумента х из области определения функции, при которых функция обращается в нуль, называются нулями функции.
Вывод: Нулями функции являются абсциссы точек пересечения графика функции с осью абсцисс.
Пример: Определить промежутки знакопостоянства и нули функции  , заданной на
, заданной на 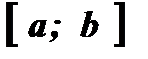 .
.
| а |
| х1 |
| О |
| х2 |
| х3 |
| b |
| х |
| у |
Значения аргумента х1, х2, х3 - нули функции  , так как
, так как 
 ;
;  .
.
Ограниченность функций
Определение: Функция  называется ограниченной, если существуют два числа т и М такие, что все значения функции удовлетворяют условию
называется ограниченной, если существуют два числа т и М такие, что все значения функции удовлетворяют условию  , то есть
, то есть 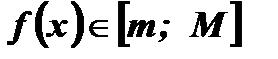 .
.
Определение: Функция  называется ограниченной сверху, если существует число М такое, что все значения функции удовлетворяют условию
называется ограниченной сверху, если существует число М такое, что все значения функции удовлетворяют условию
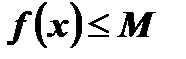 , то есть
, то есть 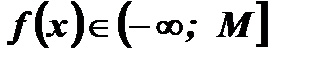 .
.
| х |
| у |
| у |
| х |
| М |
| М |
| т |
 называется ограниченной снизу, если существует число т такое, что все значения функции удовлетворяют условию
называется ограниченной снизу, если существует число т такое, что все значения функции удовлетворяют условию  , то есть
, то есть  .
.
| у |
| у |
| х |
| х |
| т |
 - ограниченная функция
- ограниченная функция 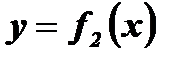 - ограниченная сверху, но неограниченная снизу функция
- ограниченная сверху, но неограниченная снизу функция
 - ограниченная снизу, но
- ограниченная снизу, но  - неограниченнаясверху неограниченная сверху функция и снизу функция
- неограниченнаясверху неограниченная сверху функция и снизу функция
Упражнения:
1. Выяснить, является ли функция четной или нечетной:
а) 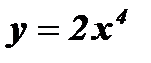 ; б)
; б) 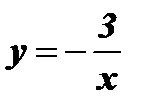 ; в)
; в)  ; г)
; г)  ;
;
2. Найти область определения функции, заданной формулой:
| х |
| у |
 ; б)
; б)  ; в)
; в) 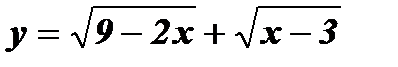 .
.
3. Дана функция  на отрезке
на отрезке  .
.
Найти обратную ей функцию и ее область определения.
4. Исследовать функцию, заданную графиком:
Схема исследования функции
- Область определения функции.
- Множество значений функции.
- Четность, нечетность функции.
- Монотонность функции.
- Обратимость функции.
- Нули функции.
- Промежутки знакопостоянства функции.
- Ограниченность функции.
Линейная функция, ее свойства и графики
Определение : Линейной функцией называется функция вида  , где x – независимая переменная, k, b – некоторые числа.
, где x – независимая переменная, k, b – некоторые числа.
Замечание: Графиком линейной функции является прямая.
1. Область определения функции  :
:  .
.
2. Множество значений функции  :
:  .
.
3. Функция  не является ни четной, ни нечетной, так как
не является ни четной, ни нечетной, так как
 ;
; 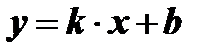 f (- х) = k ∙ (- х) + b = - k ∙ x + b;
f (- х) = k ∙ (- х) + b = - k ∙ x + b;
 и
и  .
.
4.

|
| х |
| у |

|
| х |
| у |
| l |
| l |
Рис. 1. Рис. 2.
Определение: Угловым коэффициентом прямой называется тангенс угла наклона прямой к положительному направлению оси абсцисс.
a - угол наклона прямой l к положительному направлению оси Ох.
k = tga - угловой коэффициент прямой l.
 Þ
Þ  – монотонно возрастающая функция (Рис. 1.)
– монотонно возрастающая функция (Рис. 1.)
 Þ
Þ  – монотонно убывающая функция (Рис. 2.)
– монотонно убывающая функция (Рис. 2.)
5. Функция  является обратимой:
является обратимой:
 ;
; 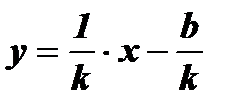 - функция, обратная для
- функция, обратная для  .
.
6.
| __ |
| х |
| + |
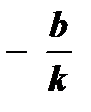
|
| __ |
| х |

|
| + |
 ;
;  - нуль функции
- нуль функции  (k ¹ 0).
(k ¹ 0).
7.
Рис. 3. Рис. 4.
 ;
;  ;
;  ;
;  ;
;
 y < 0;
y < 0;  y > 0;
y > 0;
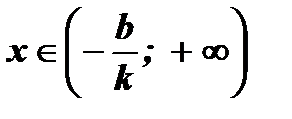 y > 0.
y > 0. 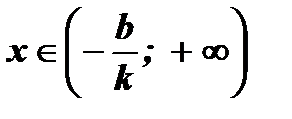 y < 0.
y < 0.
8. Функция неограниченная: 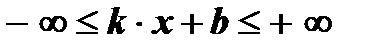
9. При х = 0 у = b.
 – точка пересечения прямой с осью Оу.
– точка пересечения прямой с осью Оу.
b – начальная ордината – отрезок, отсекаемый прямой на оси Оу.
| х |
| у |
| b > 0 |
| (0; b) |
| х |
| у |
| b < 0 |
| (0; b) |
Рис. 5. Рис. 6.
Частные случаи линейной функции  .
.
1. k = 0; y = b (у = const);
2. b = 0, k ¹ 0; y = k x – прямая пропорциональность.
Пример :
х
О
у
- 2
a
х
О
у
- 1
a
- 1


Рис.1 Рис. 2
| х |
| О |
| у |
| - 1 |
| a |
| х |
| О |
| у |
| - 2 |
| a |
| - 1 |


Рис. 3 Рис. 4
| х |
| у |
| - 1 |
| у = 0, a = 0 |
| х |
| a |
| - 1 |
| у |


Рис. 5 Рис. 6
5. Степенная функция, ее свойства и графики
Определение: Функция вида  , где a Î R, называется степенной функцией.
, где a Î R, называется степенной функцией.
 (a - натуральноечетное число )
(a - натуральноечетное число )
1. Область определения функции:  (любое действительное число можно возвести в квадрат).
(любое действительное число можно возвести в квадрат).
2. Множество значений функции: 
(при возведении в квадрат любого действительного числа получается неотрицательное число).

 ;
;
х = 0 у = 0;

 .
.
| х |
| у |
| -1 |
| -2 |
| -3 |
3. Функция является четной, так как ее область определения симметрична относительно начала координат и для любого х Î R выполняется равенство 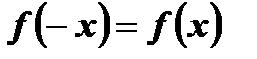 .
.
 .
.
Вывод: График функции симметричен относительно оси ординат.
4. Функция не является монотонной, так как она убываетпри  ивозрастаетпри
ивозрастаетпри  .
.
5. Функция не является обратимой, так как не является монотонной.
6. у = 0; х 2 = 0; х = 0 - нуль функции.
7.  у > 0;
у > 0;
 у > 0.
у > 0.
8. Функция является ограниченной снизу, так как у ³ 0.
Замечание: Графиком функции  является парабола.
является парабола.
| х |
| у |
| -2 |
| -8 |
 (a - натуральное нечетное число )
(a - натуральное нечетное число )
1. Область определения функции: 
(любое действительное число можно возвести в куб).
2. Множество значений функции:  :
:

 ;
;
х = 0 у = 0;

 .
.
Вывод: График функции проходит через начало координат, расположен в первой и третьей координатных четвертях.
3. Функция является нечетной, так как ее область определения симметрична относительно начала координат и для любого х Î R выполняется равенство  .
.
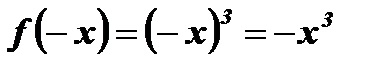 .
.
Вывод: График функции симметричен относительно начала координат.
4. Функция является монотонно возрастающей на всей области определения.
5. Функция  имеет обратную функцию
имеет обратную функцию 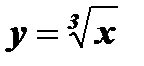 , так как монотонна.
, так как монотонна.
6. у = 0; х 3 = 0; х = 0 - нуль функции.
7.  у < 0;
у < 0;  у > 0.
у > 0.
8. Функция является неограниченной сверху и снизу.
Замечание: Графиком функции  является кубическая парабола.
является кубическая парабола.
Вывод:
1. Функция  , где a - натуральное четное число, имеет обратную функцию
, где a - натуральное четное число, имеет обратную функцию  при
при  .
.
2. Функция 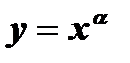 , где a - натуральное нечетное число, имеет обратную функцию
, где a - натуральное нечетное число, имеет обратную функцию  при
при  .
.
 (a - дробное четное число)
(a - дробное четное число)
1. Область определения функции:  .
.
(Арифметический квадратный корень можно извлечь только из неотрицательного числа).
2. Множество значений функции:  .
.
(Приизвлечении арифметического квадратного корня из неотрицательного числа получается неотрицательное число).
х = 0 у = 0;

 .
.
Вывод: График функции проходит через начало координат, расположен в первой координатной четверти.
3. Функция ни четная, ни нечетная, так как область определения функции не является симметричной относительно начала координат.
4. Функция является монотонно возрастающей.
5. Функция обратима, так как монотонна.
6. у = 0; 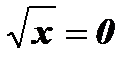 ; х = 0 - нуль функции.
; х = 0 - нуль функции.
7.  у > 0.
у > 0.
8.
| х |
| у |
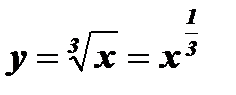 (a - дробное нечетное число )
(a - дробное нечетное число )
1. Область определения функции:  .
.
(Существует корень нечетной степени из отрицательного числа).
2. Множество значений функции:  , так как
, так как

 ;
;
х = 0 у = 0;

 .
.
Вывод: График функции проходит через начало координат, расположен в первой и третьей координатных четвертях.
3. Функция является нечетной, так как ее область определения симметрична относительно начала координат и для любого 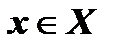 выполняется равенство
выполняется равенство  ,
,  .
.
Вывод: График функции симметричен относительно начала координат.
4. Функция является монотонно возрастающей на всей области определения.
5. Функция 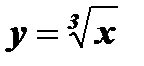 имеет обратную функцию у = х 3, так как монотонна.
имеет обратную функцию у = х 3, так как монотонна.
6. у = 0;  х 3; х = 0 - нуль функции.
х 3; х = 0 - нуль функции.
7.  у < 0;
у < 0;  у > 0.
у > 0.
8. Функция является неограниченной.
| х |
| у |
| - 2 |
| - 1 |
| - 1 |
| - 8 |
 (a - отрицательное четное число )
(a - отрицательное четное число )
1. Область определения функции:  .
.
2. Множество значений функции:  , так как
, так как

 ;
; 
 .
.
Вывод: График функции расположен в первой и второй координатных четвертях.
3. Функция является четной, так как ее область определения симметрична относительно начала координат и для любого  выполняется равенство
выполняется равенство  .
.
 .
.
Вывод: График функции симметричен относительно оси ординат.
4. Функция не является монотонной, так как она возрастает при  иубывает при
иубывает при  .
.






