Степени. Корни.
Определения степеней:
1. a n = a × a × … × a, n Î N.
2. a1 = a
3. а 0 = 1, 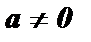 (0 0 - не имеет смысла ).
(0 0 - не имеет смысла ).
4. 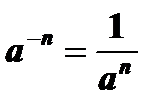 ,
,  .
.
5. 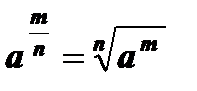 , a ³ 0, n Î N, т Î Z.
, a ³ 0, n Î N, т Î Z.
Свойства степеней:
Четная степень отрицательного числа есть число положительное.
Нечетная степень отрицательного числа есть число отрицательное.
Любая степень положительного числа есть число положительное.
4. 0 n = 0, nÎ N.
5. 1 n = 1, nÎ N.
6. 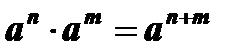 .
.
7. 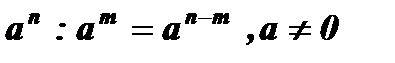 .
.
8.  .
.
9. 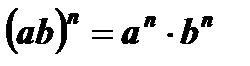 .
.
10. 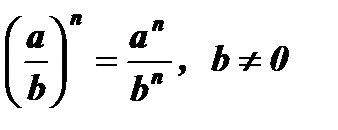 .
.
Определения корней:
1. 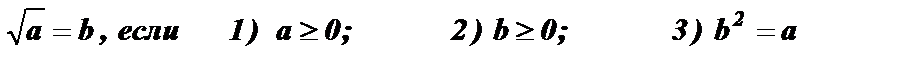 .
.
2. 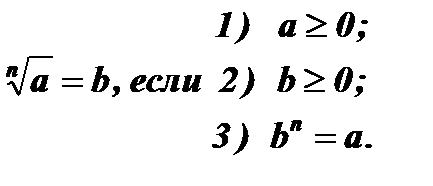
Свойства корней:
1. 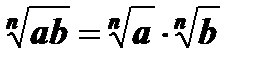 , а ³ 0, b ³ 0.
, а ³ 0, b ³ 0.
2. 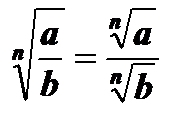 , а ³ 0, b > 0.
, а ³ 0, b > 0.
3.  , а ³ 0, nÎ N, kÎ N.
, а ³ 0, nÎ N, kÎ N.
4. 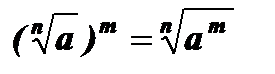 , а ³ 0, nÎ N, тÎ N.
, а ³ 0, nÎ N, тÎ N.
5.  , а ³ 0, nÎ N, тÎ N, kÎ N.
, а ³ 0, nÎ N, тÎ N, kÎ N.
6. При любом значении а  .
.
2. Числовая функция: область определения, множество значений, способы задания
Применение математики к изучению законов природы и к использованию их в технике заставило ввести в математику понятия постоянной и переменной величин. Все величины, изучаемые в математике, делятся на постоянные и переменные.
Определение: Величина называется постоянной, если она в условиях данного эксперимента сохраняет одно и то же значение.
(Постоянная – const. (лат.))
Пример: Постоянными величинами являются:
Длина радиуса данной окружности;
Температура кипения воды при постоянном давлении.
Замечание: Некоторые постоянные сохраняют свое числовое значение при любых условиях, их называют абсолютными постоянными.
Пример: Абсолютными постоянными величинами являются:
Сумма углов треугольника;
Скорость света в пустоте;
Количество секунд в минуте;
4. p = 3,14…;
5. е = 2,718281828459045….
Определение: Величина называется переменной, если она в условиях данного эксперимента может принимать различные значения.
Пример: Скорость камня, брошенного вверх, является переменной величиной.
В практических задачах часто рассматриваются переменные величины, которые связаны между собой так, что значения одной определяют значения другой.
Пример: Объем V шара радиуса R определяется по формуле 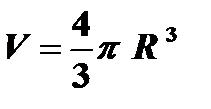 .
.
 ; p – постоянные величины;
; p – постоянные величины;
R – независимая переменная;
V – зависимая переменная.
Определение: Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.
х – независимая переменная, аргумент;
 – зависимая переменная, значение функции;
– зависимая переменная, значение функции;
Пример: V = f (R) – объем является функцией радиуса, то есть 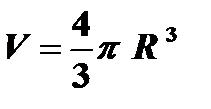
Определение: Областью определения функции называются все значения аргумента x, при которых функция определена (то есть имеет числовое значение).
D (f) = Х – область определения функции.
Определение: Множеством значений функции называются все значения зависимой переменной y при x из области определения функции.
E (f) = У – множество значений функции.
Пример: Найти область определения функции:
1. 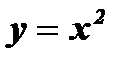
При любом действительном значении х функция у так же выражается действительным числом, следовательно, функция определена при любом значении 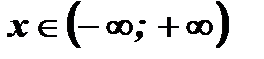 . Следовательно,
. Следовательно,  .
.
2. 
Знаменатель дроби обращается в нуль при х = 0. Функция принимает действительные значения при всех х, кроме х = 0. Следовательно,
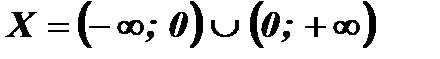 .
.
3. 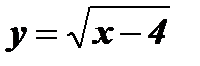
Функция имеет смысл только в том случае, когда подкоренное выражение больше нуля или равно нулю (неотрицательное), то есть  . Следовательно,
. Следовательно,  .
.
Замечание:
1. При нахождении области определения дробной функции нужно исключить значения аргумента, при которых знаменатель дроби обращается в нуль. Для этого знаменатель дроби приравнивается к нулю. Если полученное уравнение имеет корни, то они исключаются из области определения функции.
2. Если функция содержит корень четной степени, то при нахождении области определения нужно исключить значения аргумента, при которых подкоренное выражение принимает отрицательные значения. В область определения функции войдут значения аргумента, при которых подкоренное выражение принимает неотрицательные значения, то есть решения соответствующего неравенства.
Способы задания функции
Замечание: Функция считается заданной, если известна область определения функции и указано правило, по которому для каждого значения аргумента из области определения можно найти соответствующее значение функции.
1. Табличный способ: значения аргумента и соответствующие значения функции записаны в виде таблицы.
Достоинства: простой способ.
Недостатки: не дает полного представления о функции; не является наглядным.
Замечание: В результате экспериментального изучения какого-нибудь явления или процесса (испытание самолетов, моторов, урожайности семян) всегда устанавливается функциональная зависимость между переменными в виде таблицы.
2. Графический способ: функция задана с помощью графика.
Определение: Графиком функции называется множество точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
Достоинства: наглядный способ.
Недостатки: небольшая точность при определении значений функции при данных значениях аргумента; ограниченность промежутка, на котором может быть построен график функции.
Замечание: Иногда табличный и графический способы задания функции являются единственно возможными, в других случаях используются как дополнительные. Метеорологи составляют таблицы выпавших осадков.В медицине о работе сердца судят по кардиограмме, которую создает прибор – кардиограф; вибратор регистрирует колебания различных сооружений (мостов, судов, зданий).
3. Аналитический способ: функция задана с помощью формулы  , где
, где
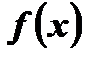 – выражение с переменной х.
– выражение с переменной х.
Достоинства: значения функции могут быть вычислены для любого значения аргумента из области определения функции.
Недостатки: не является наглядным.
Замечание:
1. Для аналитически заданной функции иногда не задают область определения явно. В таком случае область определения функции  совпадает с областью определения выражения
совпадает с областью определения выражения  .
.
2. Одной и той же формулой можно задать различные функции, изменяя область определения.
3. Функция может быть задана различными формулами на различных промежутках области определения.
Пример:
1. Если функция задана формулой 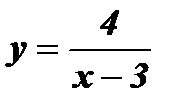 без указания области ее определения, то предполагается, что область определения этой функции – множество всех действительных чисел, кроме числа 3 (при х = 3 выражение
без указания области ее определения, то предполагается, что область определения этой функции – множество всех действительных чисел, кроме числа 3 (при х = 3 выражение 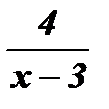 не имеет смысла).
не имеет смысла).
2. Различными функциями являются 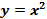 , х Î R, и
, х Î R, и 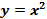 , х Î N.
, х Î N.
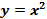 , х Î R, – квадратичная функция;
, х Î R, – квадратичная функция;
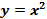 , х Î N, – числовая последовательность вида 1; 4; 9; 16;…; п2;….
, х Î N, – числовая последовательность вида 1; 4; 9; 16;…; п2;….
3. 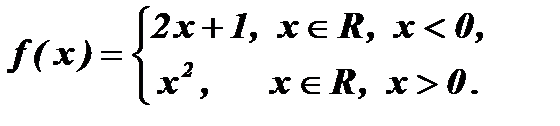
4. 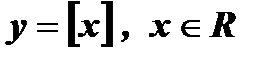 .
.  – целая часть числа х, то есть наибольшее целое число, не превосходящее х.
– целая часть числа х, то есть наибольшее целое число, не превосходящее х. 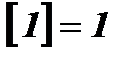 ;
;  ;
; 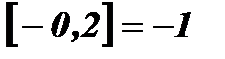 ;
;  .
.
4. Словесное описание: если формулу, задающую функцию, записать сложно или невозможно, пользуются словесным описанием способа, задающего функцию.
Пример: Функция Дирихле:
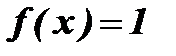 , если х – рационально;
, если х – рационально;  , если х – иррационально.
, если х – иррационально.
Упражнения:
- Найти область определения функции:
а)  ; б)
; б)  ; в)
; в) 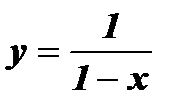 ; г)
; г) 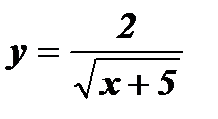 ;
;
д) 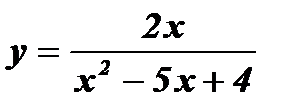 ; е)
; е) 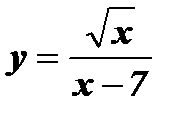 ; ж)
; ж)  ; з)
; з)  .
.
- Дана функция
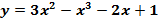 . Найти
. Найти 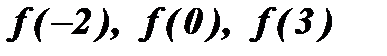 .
.
Свойства числовых функций
Четность, нечетность функций
Определение: Функция  называется четной, если она обладает следующими свойствами:
называется четной, если она обладает следующими свойствами:
1) область определения этой функции симметрична относительно начала координат, то есть  для любого
для любого  ;
;
2) для любого значения х, принадлежащего области определения этой функции, выполняется равенство 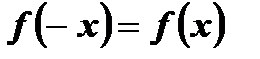 .
.
Вывод:
1. Если точка 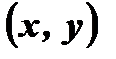 принадлежит графику четной функции, то точка
принадлежит графику четной функции, то точка  так же принадлежит графику этой функции.
так же принадлежит графику этой функции.
2.
| у |
| х |
| - 1 |
| - 2 |
| О |
| у |
| х |
| х |
| - х |
| у |
| О |
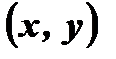 и
и  , принадлежащих графику четной функции, симметрична относительно оси ординат, следовательно, график любой четной функции симметричен относительно оси ординат (Рис. 1).
, принадлежащих графику четной функции, симметрична относительно оси ординат, следовательно, график любой четной функции симметричен относительно оси ординат (Рис. 1).
Рис. 1. Рис. 2.
Пример: 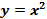 – четная функция, так как, во-первых, область определения этой функции
– четная функция, так как, во-первых, область определения этой функции 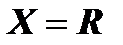 симметрична относительно начала координат; во-вторых, для любого
симметрична относительно начала координат; во-вторых, для любого  выполняется равенство
выполняется равенство 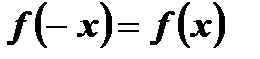 .
.
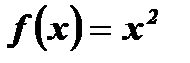 ,
,  (Рис. 2).
(Рис. 2).
Определение: Функция  называется нечетной, если она обладает следующими свойствами:
называется нечетной, если она обладает следующими свойствами:
1) область определения этой функции симметрична относительно начала координат, то есть  для любого
для любого  ;
;
2)
| у |
| х |
| х |
| - х |
| у |
| О |
| - у |
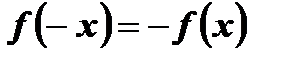 .
.
Вывод:
1. Если точка  принадлежит графику нечетной функции, то точка
принадлежит графику нечетной функции, то точка  так же принадлежит графику этой функции.
так же принадлежит графику этой функции.
2. Так как любая пара точек  и
и 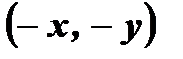 , принадлежащих графику нечетной функции, симметрична относительно начала координат, следовательно, график любой нечетной функции симметричен относительно начала координат.
, принадлежащих графику нечетной функции, симметрична относительно начала координат, следовательно, график любой нечетной функции симметричен относительно начала координат.
Пример:  – нечетная функция, так как, во-первых, область определения этой функции
– нечетная функция, так как, во-первых, область определения этой функции  симметрична относительно начала координат; во-вторых, для любого
симметрична относительно начала координат; во-вторых, для любого  выполняется равенство
выполняется равенство  .
.
 ,
,  .
.
Пример: Исследовать на четность и нечетность функции:
1)  ;
;
Область определения данной функции 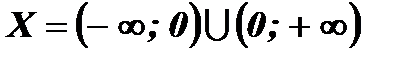 симметрична относительно начала координат. Найдем
симметрична относительно начала координат. Найдем 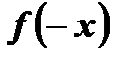 и сравним с
и сравним с  :
:  ,
,  .
.
Следовательно,  является четной функцией.
является четной функцией.
2) 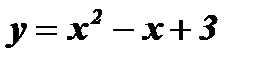 ;
;
Область определения данной функции  симметрична относительно начала координат. Найдем
симметрична относительно начала координат. Найдем 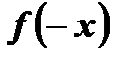 и сравним с
и сравним с  :
:
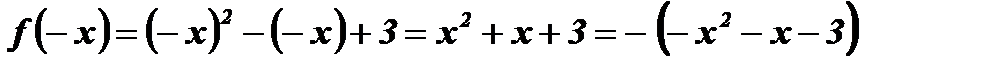 ,
,
 и
и  . Следовательно,
. Следовательно, 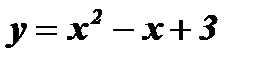 не является ни четной, ни нечетной функцией.
не является ни четной, ни нечетной функцией.
3) 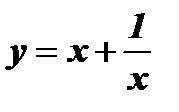 .
.
Область определения данной функции 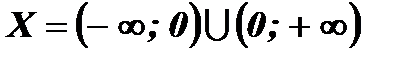 симметрична относительно начала координат. Найдем
симметрична относительно начала координат. Найдем 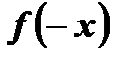 и сравним с
и сравним с  :
: 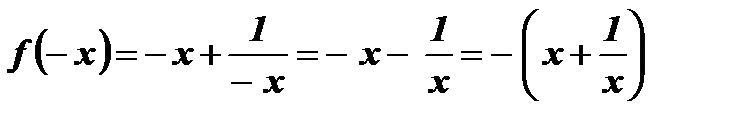 ,
, 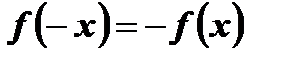 .
.
Следовательно, 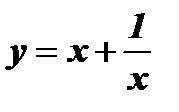 является нечетной функцией.
является нечетной функцией.
Монотонность функций
Определение: Функция  называется возрастающей на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее значение функции (Рис. 1).
называется возрастающей на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее значение функции (Рис. 1).
| у |
| х |
| х2 |
| х1 |
| у2 |
| О |
| у1 |
| х3 |
| у3 |
| у |
| х |
| х2 |
| х1 |
| у2 |
| О |
| у1 |
| х3 |
| у3 |
 называется убывающей на промежутке Х, если большему значению аргумента из этого промежутка соответствует меньшее значение функции. (Рис. 2)
называется убывающей на промежутке Х, если большему значению аргумента из этого промежутка соответствует меньшее значение функции. (Рис. 2)
Рис. 1. Рис. 2
Вывод: График возрастающей функции - восходящая кривая, график убывающей функции - нисходящая кривая при перемещении вдоль оси абсцисс в положительном направлении.
Определение: Функция только возрастающая или только убывающая на данном промежутке называется монотонной на этом промежутке.
| х |
| у |
| О |
| х |
| у |
| О |
| х |
| у |
| О |

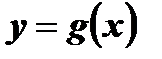
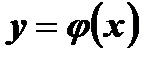
монотонновозрастающая монотонноубывающая не монотонная функция функция функция
Обратимость функций
Определение: Функция называется обратимой (имеет обратную функцию), если она принимает каждое свое значение один раз.
| у |
| х |
| О |
| а |
| b |
| c |
| d |
| х |
| у |
| у |
| х |
| О |
| а |
| b |
| c |
| d |
| х3 |
| у1 |
| х2 |
| х1 |
Рис. 1:  Рис. 2:
Рис. 2: 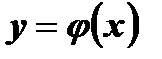
Функции  (Рис. 1)и
(Рис. 1)и 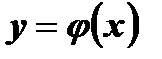 ( Рис. 2) определены на
( Рис. 2) определены на 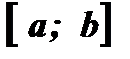 и имеют множество значений
и имеют множество значений 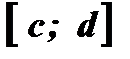 .
.
Функция  принимает каждое свое значение один раз, то есть у = f (х) -обратимая функция.
принимает каждое свое значение один раз, то есть у = f (х) -обратимая функция.
Функция 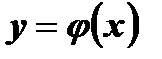 принимает некоторые свои значения не один раз, то есть у = j (х) -необратимая функция.
принимает некоторые свои значения не один раз, то есть у = j (х) -необратимая функция.
Вывод: Обратима только монотонная функция.
Пример: Найти функцию обратную функции  . Построить графики взаимно обратных функций.
. Построить графики взаимно обратных функций.
Решение:
1. Из формулы 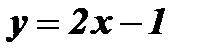 выразим х через у:
выразим х через у: 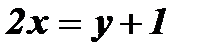 ;
;  ;
; 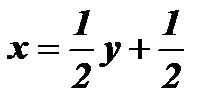 .
.
В полученной формуле поменяем местами х и у: 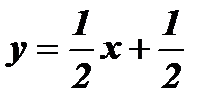 .
.
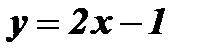 и
и 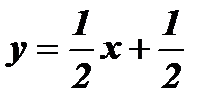 - взаимно обратные функции.
- взаимно обратные функции.
2.
| О |
| х |
| у |
| - 3 |
| - 4 |
| - 5 |
| - 4 |
| - 5 |
| - 2 |
| l1 |
| l2 |
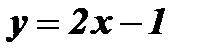 и
и 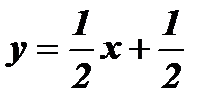 :
:
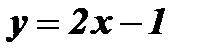 х - 2 2
х - 2 2
у - 5 3
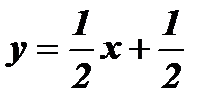
х - 5 3
у - 2 2
График функции  - прямая l1 проходит через точки ( - 2; - 5) и (2;3).
- прямая l1 проходит через точки ( - 2; - 5) и (2;3).
График функции 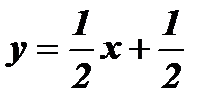 - прямая l2 проходит через точки ( - 5; - 2) и (3;2).
- прямая l2 проходит через точки ( - 5; - 2) и (3;2).
Прямая  является осью симметрии прямых l1 и l2.
является осью симметрии прямых l1 и l2.
Вывод:
1. Чтобы получить функцию, обратную даннойфункции  , надо из формулы
, надо из формулы  выразить х через у и в полученной формуле поменять местами х и у.
выразить х через у и в полученной формуле поменять местами х и у.
2. Графики взаимно обратных функций симметричны относительно прямой 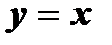 .
.






