6.
| х |
| у |
| - 1 |
| - 2 |
| - 3 |
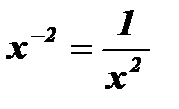 = 0 - уравнение корней не имеет, нулей функции нет.
= 0 - уравнение корней не имеет, нулей функции нет.
Вывод: График функции не пересекает ось Ох
7.  у > 0;
у > 0;  у > 0.
у > 0.
8. Функция является ограниченной снизу, так как у > 0.
| х | 
| 
| |||
| у | 
| 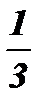
|
| -1 |
| х |
| у |
| -1 |
| -2 |
| -2 |
| -3 |
| -4 |
| -5 |
| -6 |
| -7 |
| -8 |
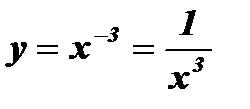 (a - отрицательное нечетное число )
(a - отрицательное нечетное число )
1. Область определения функции:  .
.
2. Множество значений функции: 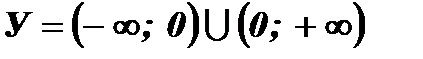 , так как
, так как 
 ;
;

 .
.
Вывод: График функции расположен в первой и третьей координатных четвертях.
3. Функция является нечетной, так какее область определения симметрична относительно начала координат и для любого  выполняется равенство
выполняется равенство  .
. 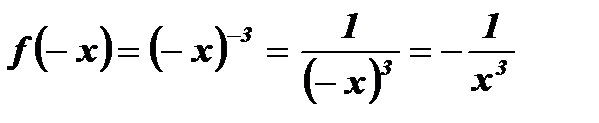 .
.
Вывод: График функции симметричен относительно начала координат.
4. Функция является монотонной, так как убывает при 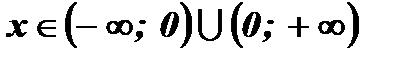 .
.
5. Функция является обратимой, так как является монотонной.
6. у = 0; 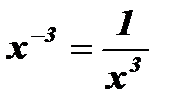 = 0 уравнение корней не имеет, нулей функции нет.
= 0 уравнение корней не имеет, нулей функции нет.
Вывод: График функции не пересекает ось Ох.
| х | 
| 
| |||
| у | 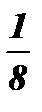
| 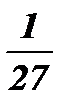
|
7.  у < 0;
у < 0;  у > 0.
у > 0.
8. Функция является неограниченной сверху и снизу .
Упражнения:
1. Дана функция 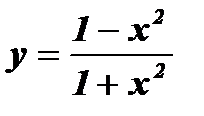 . Найти: f (0), f ( - 1), f (1), f (
. Найти: f (0), f ( - 1), f (1), f (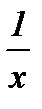 ).
).
2. Найти область определения функции:
1) 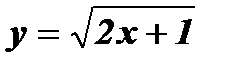 ; 2)
; 2) 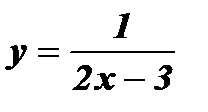 ; 3)
; 3) 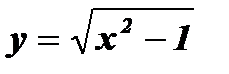 .
.
Квадратичная функция, ее свойства и графики
Определение: Функция вида 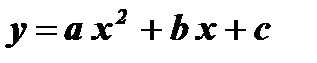 , где a, b, c - действительные числа, причем а ¹ 0, называется квадратичной функцией.
, где a, b, c - действительные числа, причем а ¹ 0, называется квадратичной функцией.
Замечание: Графиком квадратичной функции 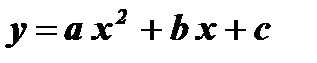 является парабола, по-разному расположенная относительно координатных осей.
является парабола, по-разному расположенная относительно координатных осей.
Частные случаи:
| у |
| х |
| у |
| у |
| х |
| х |
Рис. 1 Рис. 2 Рис. 3
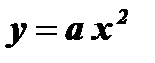 (b = 0, c = 0)
(b = 0, c = 0) 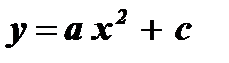 (b = 0)
(b = 0) 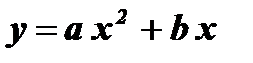 (c = 0)
(c = 0)
Общий случай: 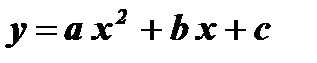 (b ¹ 0, c ¹ 0)
(b ¹ 0, c ¹ 0)
- Область определения функции: Х = R.
- Координаты вершины параболы А (т, п) определяются по формулам:
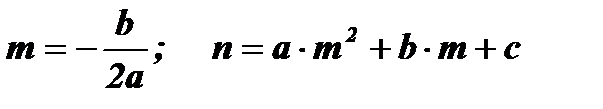 .
.
- Множество значений функции: при а > 0
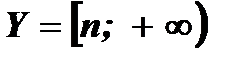 ;
;
при а < 0 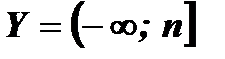 .
.
- Функция ни четная ни нечетная, так как
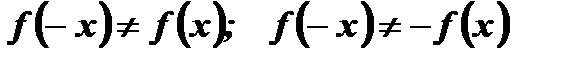 .
.
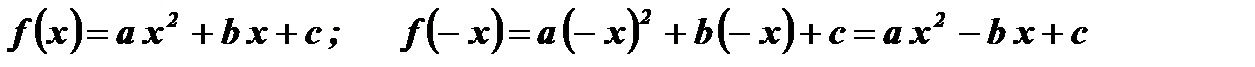 .
.
| х |
| у |
| т |
| п |
| т |
| п |
| т |
| т |
| п |
| п |
| у |
| х |
Рис. 4 Рис. 5
а > 0, b ¹ 0, c ¹ 0 а < 0, b ¹ 0, c ¹ 0
- Функция не монотонная:
при а > 0 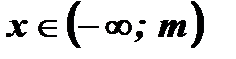 у - убывает;
у - убывает;
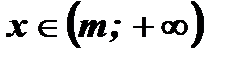 у - возрастает;
у - возрастает;
при а < 0 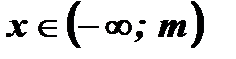 у - возрастает;
у - возрастает;
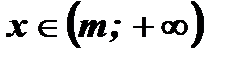 у - убывает.
у - убывает.
- Функция не обратимая, так как не монотонная.
- Нули функции:
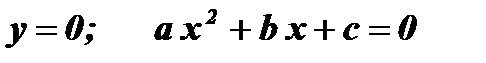 ;
;
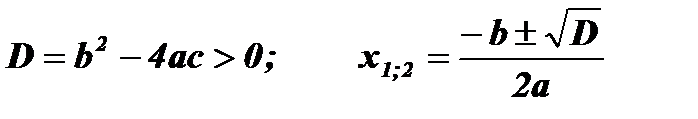 ; х1;2 - нули функции;
; х1;2 - нули функции;
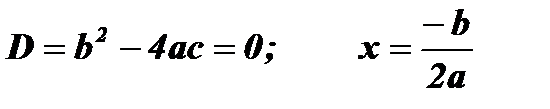 ; х - нуль функции;
; х - нуль функции;
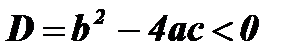 ; нулей функции нет.
; нулей функции нет.
- Промежутки знакопостоянства:
| х |
| х |
| х |
| х1 |
| х2 |
| х |
| + |
| + |
| - |
| + |
| + |
| + |
| + |
| + |
Рис. 5 Рис. 6 Рис. 7
а > 0; D > 0; а > 0; D = 0; а > 0; D < 0;
| х |
| х |
| х |
| х1 |
| х2 |
| х |
| + |
| - |
| - |
| - |
| - |
| - |
| - |
| - |
Рис. 8 Рис. 9 Рис. 10
а < 0; D > 0; а < 0; D = 0; а < 0; D < 0;
- При
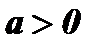 функция ограниченная снизу, так как
функция ограниченная снизу, так как 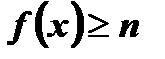 при любом
при любом 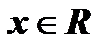 ; при
; при 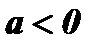 функция ограниченная сверху, так как
функция ограниченная сверху, так как 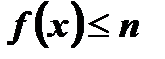 при любом
при любом 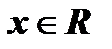 .
.
7. Уравнения с одной переменной
7.1. Уравнения, содержащие переменную под знаком модуля.
Определение: Модулем (абсолютной величиной) действительного числа а называется само число а, если 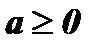 , и противоположное число - а, если
, и противоположное число - а, если 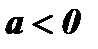 .
.
Обозначение:  - модуль числа а.
- модуль числа а.
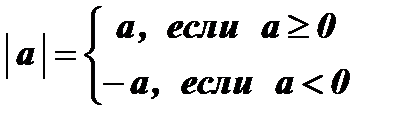
Замечание:
1. Из определения следует, что при любом действительном а 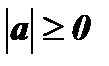 .
.
2. Модуль числа равен расстоянию от точки, изображающей данное действительное число на числовой оси, до нуля.
| - 2 |
| 3,5 |
| х |
| - 1 |
| ½ 2 ½ |
| ½- 2 ½ |
| ½ 3,5 ½ |
| ½ 0 ½ |
½- 2 ½= 2; ½ 2 ½= 2; ½ 3,5 ½= 3,5; ½ 0 ½= 0.
3. ½ b - а ½ - расстояние между точками, изображающими на числовой оси числа а и b.
| a |
| х |
| ½ b ½ |
| ½ a ½ |
| ½ b - a ½ |
| b |
| b |
| х |
| ½ а ½ |
| ½ b ½ |
| ½ b - a ½ |
| a |
½ b - а ½= b - а, если b > а ½ b - а ½= а - b, если b < а
Способы решения уравнений, содержащих переменную под знаком модуля:
1. Раскрытие модуля по определению.
2. Возведение обеих частей уравнения в квадрат.
3. Разбиение на промежутки.
Пример:
1. 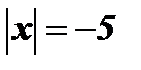 .
.
Решение:
Так как при любом х 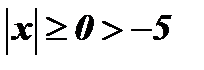 , то уравнение решений не имеет.
, то уравнение решений не имеет.
Ответ: Решений нет.
2. 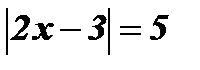 .
.
Решение:
Раскроем 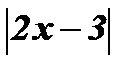 по определению:
по определению:

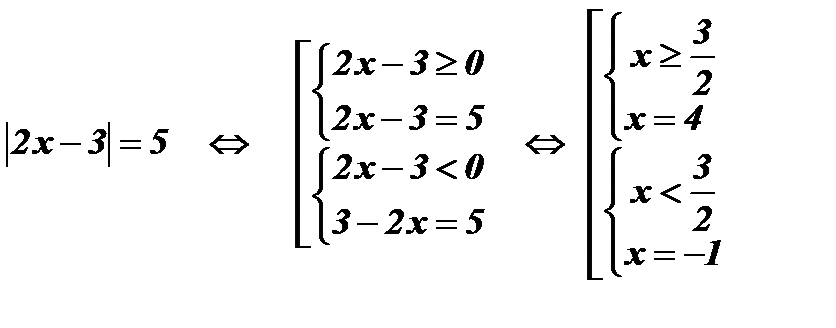
Ответ: х1 = 4; х2 = - 1.
Теорема: Если обе части уравнения 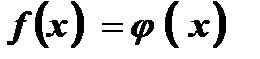 , где
, где 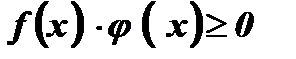 при всех значениях х из области определения уравнения, возвести в одну и ту же натуральную степень п, то получится уравнение
при всех значениях х из области определения уравнения, возвести в одну и ту же натуральную степень п, то получится уравнение  , равносильное данному.
, равносильное данному.
3. 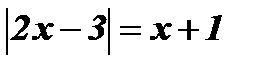 .
.
Решение:
Если х+1 < 0, то уравнение корней не имеет, так как 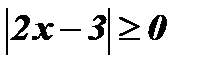 .
.
Если х+1 ≥ 0, то обе части уравнения неотрицательны, возведем их в квадрат:
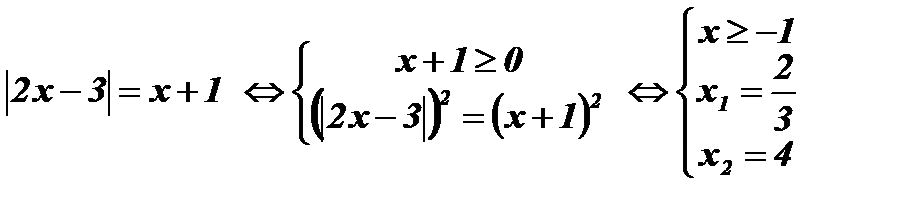
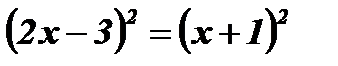 ;
; 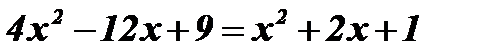 ;
; 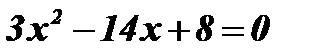 ;
;
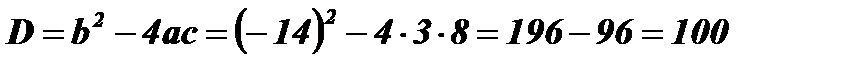 ;
;
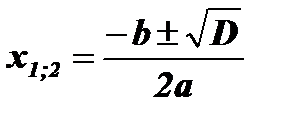 ;
; 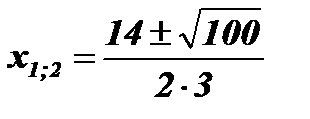 ;
; 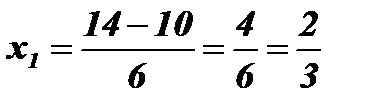 ;
; 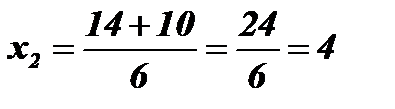 .
.
Ответ: 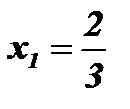 ;
; 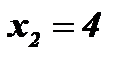 .
.
4. 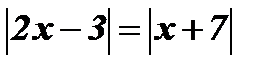 .
.
Решение:
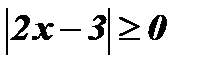 ,
, 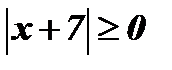 .
.
Так как обе части уравнения положительны, возведем их в квадрат:
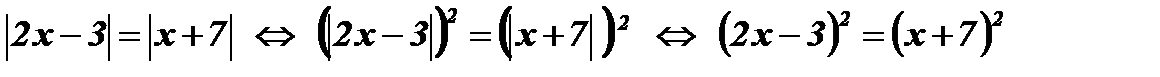 Û
Û
Û 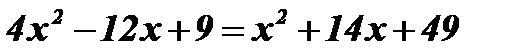 Û
Û 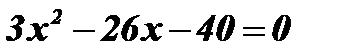 ;
;
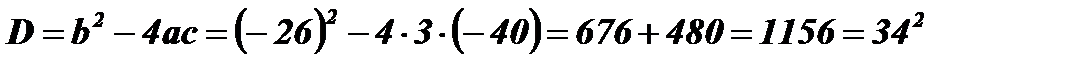 ;
;
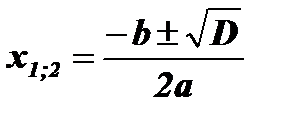 ;
; 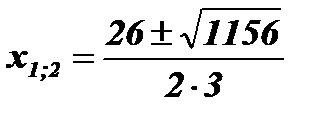 ;
;
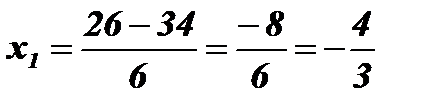 ;
; 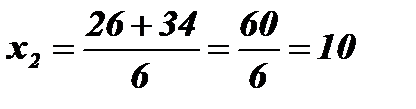 .
.
Ответ: 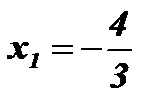 ;
; 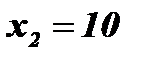 .
.
5. 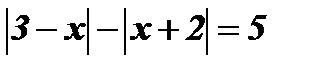 .
.
Решение:
1) На числовой прямой отметим значения х, при которых 3 – х = 0, и значения х, при которых х + 2 = 0.
3 – х = 0 при х = 3.
х + 2 = 0 при х = – 2.
2) Числовая прямая разбивается на промежутки: 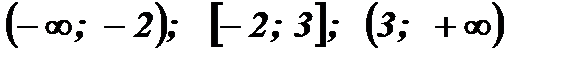 .
.
Определим знак каждого из двучленов в полученных промежутках:
r PK9fg7/cisynRo0+aqh85w5qDNOdx0EN17UQ0KF8DdNneZ56h6JjKDzjppd6PeIORSmCRo0+aqi0 7A5qDHOzx0EN35aoYZnarzFTr8nsqYzO15iPiBpKETRq9FHjSG4oj3uO7tcIAl/khprDkx3ar6H9 Gl/Cr6GSpH8vqMGyy/G6eJb7Kl5tT++j737HdfcF/K/+BwAA//8DAFBLAwQUAAYACAAAACEAQUuu m+AAAAAJAQAADwAAAGRycy9kb3ducmV2LnhtbEyPQUvDQBCF74L/YRnBm90kpTWN2ZRS1FMR2gri bZudJqHZ2ZDdJum/dzzpbea9x5tv8vVkWzFg7xtHCuJZBAKpdKahSsHn8e0pBeGDJqNbR6jghh7W xf1drjPjRtrjcAiV4BLymVZQh9BlUvqyRqv9zHVI7J1db3Xgta+k6fXI5baVSRQtpdUN8YVad7it sbwcrlbB+6jHzTx+HXaX8/b2fVx8fO1iVOrxYdq8gAg4hb8w/OIzOhTMdHJXMl60ClarOSdZf05A sL9MUx5OLCSLBGSRy/8fFD8AAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAA AAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACU AQAACwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEAc/kE0WIJAADI XwAADgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAQUuum+AA AAAJAQAADwAAAAAAAAAAAAAAAAC8CwAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAAMkM AAAAAA== ">
| 3 – х |
| х |
| х +2 |
| - 2 |
| + |
| + |
| - |
| - |
| + |
| + |
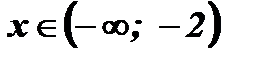
| 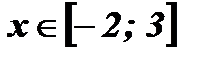
| 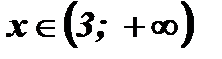
| |
| 3 – х | + | + | - |
| х +2 | - | + | + |
3) Решим уравнение на каждом промежутке:
При 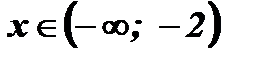
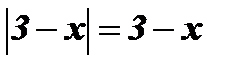 ;
; 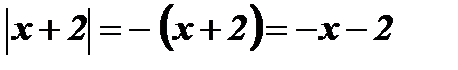 .
.
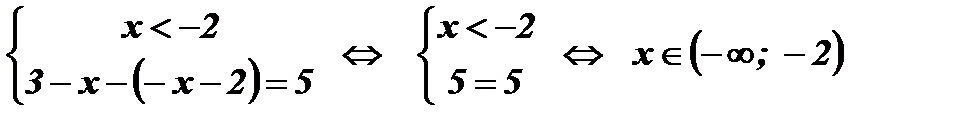 .
.
При 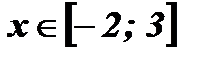
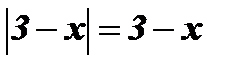 ;
; 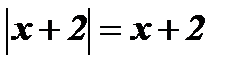 .
.
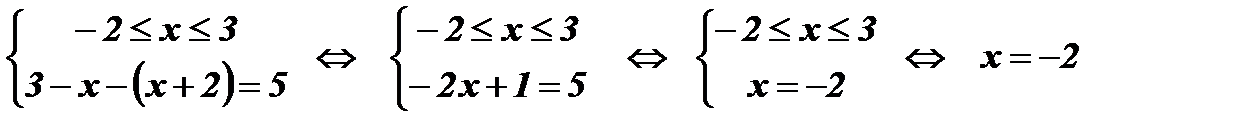 .
.
При 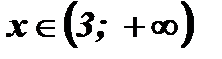
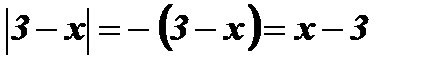 ;
; 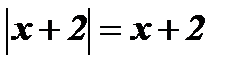 .
.
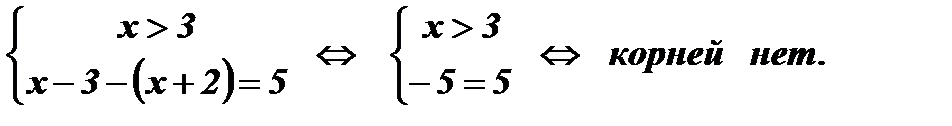
Ответ: 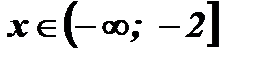 .
.
Упражнения:
1. 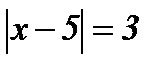 ; ;
| 2. 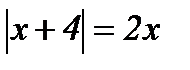 ; ;
| 3. 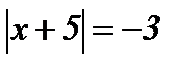 ; ;
|
4. 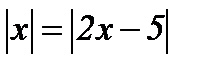 ; ;
| 5. 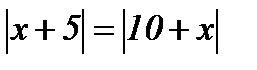 ; ;
| 6. 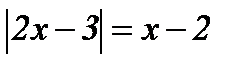 ; ;
|
7. 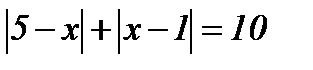 ; ;
| 8. 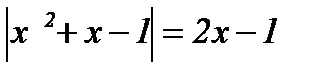 ; ;
| 9. 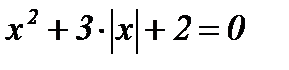 ; ;
|
10. 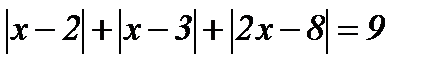 ; ;
| 11. 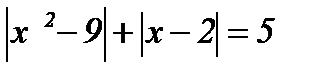 ; ;
| 12. 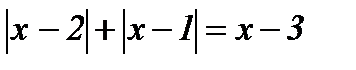 ; ;
|
13. 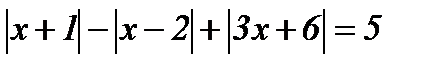 ; ;
| 14. 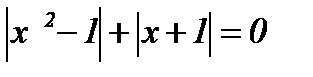 ; ;
| 15. 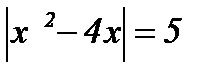 . .
|
7.2. Иррациональные уравнения
Определение: Иррациональным уравнением называется уравнение, содержащее переменную под знаком корня или под знаком операции возведения в дробную степень.
Замечание: Чтобы решить иррациональное уравнение, нужно сначала освободиться от корней, подкоренные выражения которых содержат переменную. Чаще всего этого добиваются возведением в квадрат обеих частей уравнения. Однако при этом могут появиться «посторонние» корни, которые не удовлетворяют данному иррациональному уравнению. Появление «посторонних» корней возможно при расширении области определения данного иррационального уравнения.
Вывод: При решении иррациональных уравнений необходима проверка.
Пример:
-
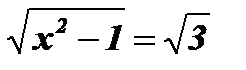 .
.
Решение:
Возведем обе части уравнения в квадрат: 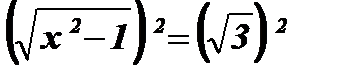 ;
;
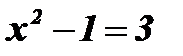 ;
; 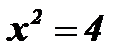 ;
; 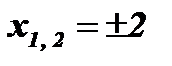 .
.
Проверка:
х1 = 2; 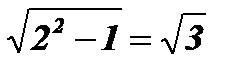 ;
;  ;
;
х2 = - 2; 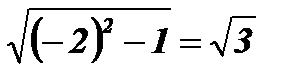 ;
;  .
.
Ответ: 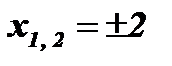 .
.
-
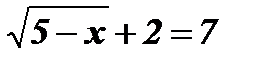 .
.
Решение:
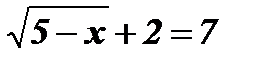 Û
Û 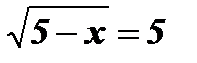 ;
;
Возведем обе части уравнения в квадрат: 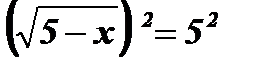 ; 5 - х = 25; х = - 20.
; 5 - х = 25; х = - 20.
Проверка:
х = - 20; 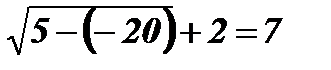 ; 7 = 7.
; 7 = 7.
Ответ: х = - 20.
-
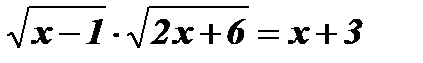 .
.
Решение:
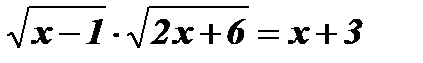 Û
Û 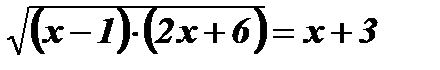 Û
Û 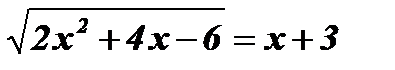 ;
;
Возведем обе части уравнения в квадрат: 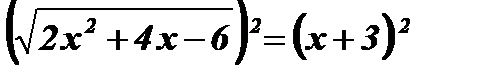 ;
;
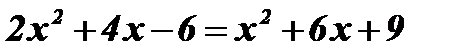 ;
; 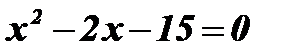 ;
;
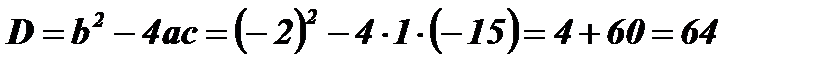 ;
;
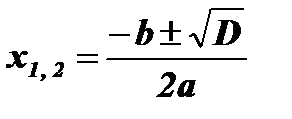 ;
;  ; х1 = - 3; х2 = 5.
; х1 = - 3; х2 = 5.
Проверка:
х1 = - 3; 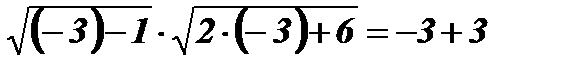 ;
; 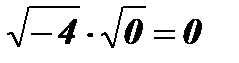 ;
; 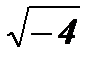 - не существует;
- не существует;
х1 = - 3 - не является корнем данного уравнения.
х2 = 5; 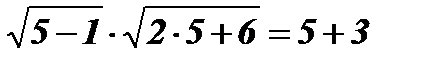 ; 8 = 8.
; 8 = 8.
Ответ: х = 5.
-
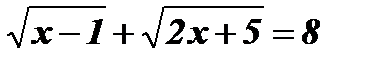 .
.
Решение:
Возведем обе части уравнения в квадрат: 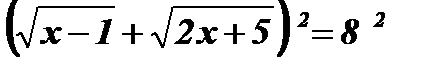 ;
;
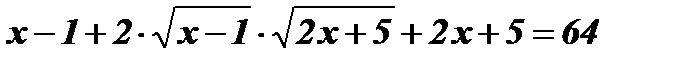 ;
; 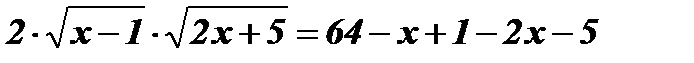 ;
;
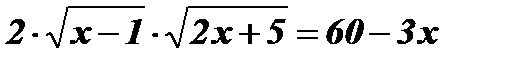 ;
;
Возведем обе части уравнения в квадрат: 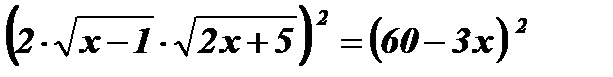 ;
;
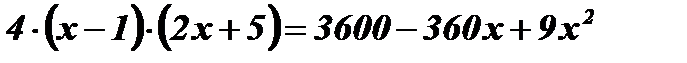 ;
; 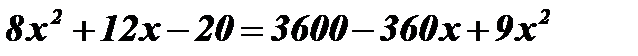 ;
;
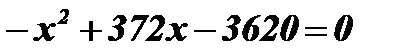 ;
;
Умножим обе части уравнения на - 1: 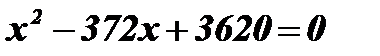 ;
;
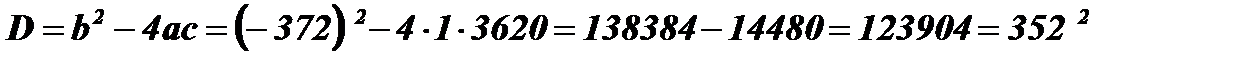 ;
;
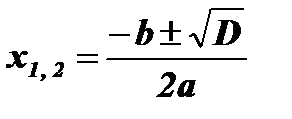 ;
; 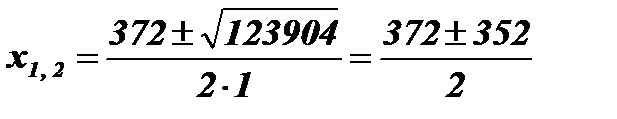 ; х1 = 10; х2 = 362.
; х1 = 10; х2 = 362.
Проверка:
х1 = 10; 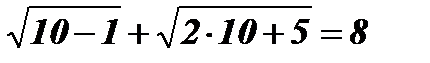 ; 8 = 8.
; 8 = 8.
х2 = 362; 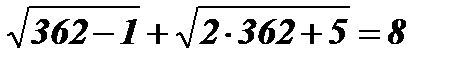 ; 19 + 27 ¹ 8.
; 19 + 27 ¹ 8.
х2 = 362 - не является корнем данного иррационального уравнения.
Ответ: х = 10.
-
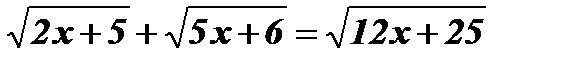 .
.
Решение:
Возведем обе части уравнения в квадрат: 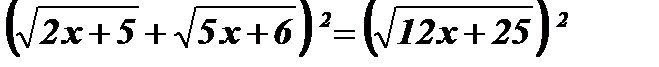 ;
;
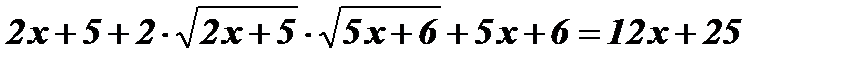 ;
; 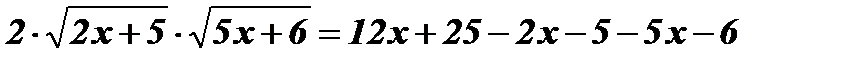 ;
;
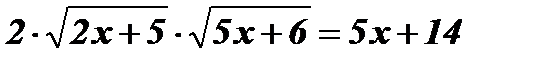 ;
;
Возведем обе части уравнения в квадрат: 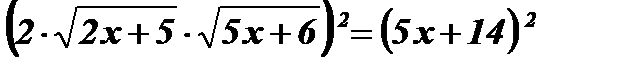 ;
;
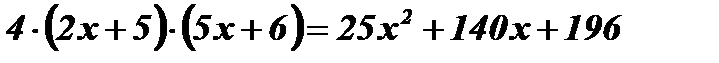 ;
; 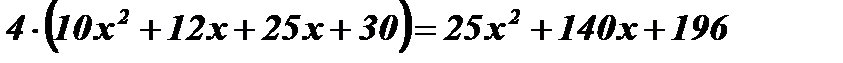 ;
;
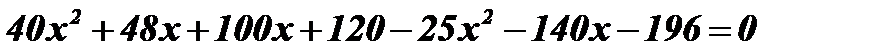 ;
; 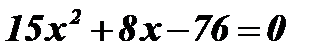 ;
;
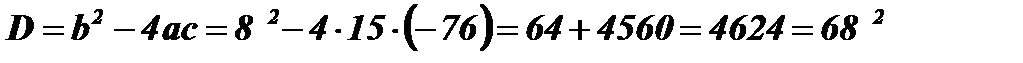 ;
;
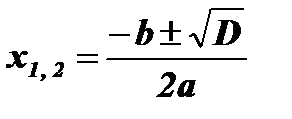 ;
; 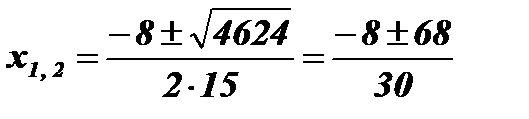 ; х1 = 2; х2 =
; х1 = 2; х2 = 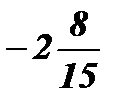 .
.
Проверка:
х1 = 2; 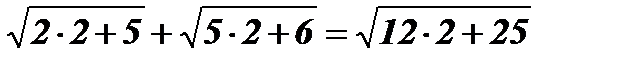 ; 3 + 4 = 7; 7 = 7.
; 3 + 4 = 7; 7 = 7.
х2 = 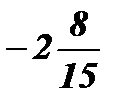 ;
; 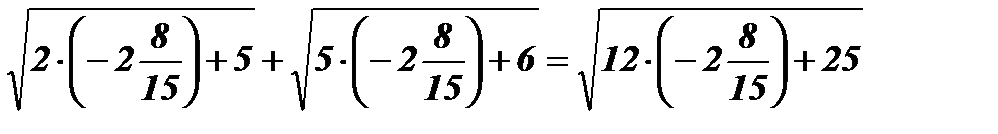 ;
;
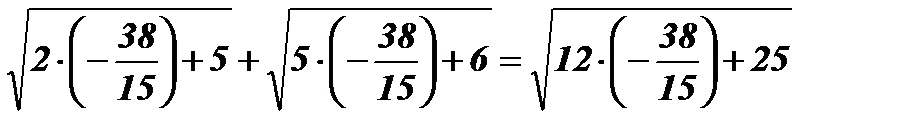 ;
;
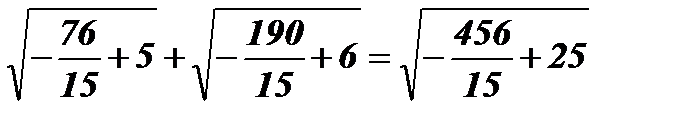 ;
; 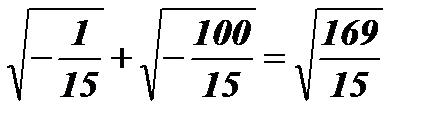 ;
;






