Чтобы приближенные решения, отыскиваемые по методу Ритца, при увеличении числа параметров сходились с точными, необходимо задать систему координатных функций, обладающих следующими свойствами:
координатные функции удовлетворяют кинематическим, существенным условиям закрепления пластины;
взятые в любом конечном числе координатные функции линейно независимы;
координатные функции должны быть непрерывны вместе с первыми производными и иметь интегрируемые квадраты вторых производных. Все эти требования выполнить нетрудно, т.к. краевые условия для функций w o, w 1 просты, а класс функций, обеспечивающий существование интегралов по области в уравнениях (5.44), весьма широк. Так, в нашем случае, координатные функции должны быть подчинены следующим краевым условиям:
на защемленном крае
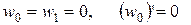(5.47)
на свободно-опертом крае
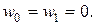(5.48)
Проверить линейную независимость координатных элементов (если она неочевидна) можно, составив определитель Грамма. Если он не равен нулю, то это требование выполнено. Линейную независимость координатных функций можно считать обеспеченной, если они выбраны в виде степенных и тем более ортогональных полиномов.
Третье условие – полноту координатных систем считаем при решении конкретной задачи выполненным.
Обычно при использовании вариационных методов в теории пластин в качестве координатных функций принимают тригонометрические, гиперболо-тригонометрические и степенные полиномы.
При выполнении расчетов на ЭВМ предпочтение следует отдать степенным полиномам. Это объясняется простотой программирования, малым временем на вычисление значений этих функций и их производных в узлах. Гиперболо-тригонометрические функции, комбинации бесселевых и других специальных функций менее удобное для расчета, чем полиномы, т.к. значения последних легко вычисляются, в то время, как для вышеуказанных балочных функций необходимо использовать таблицы или медленно сходящие ряды. В литературе не приведено убедительных доказательств того, что для расчета балочные функции удобнее полиномов. Как правило, результаты расчетов и с теми, и с другими функциями при одинаковом количестве параметров отличаются незначительно, хотя в некоторых работах показано, что лучшие результаты получаются с полиномами. Следовательно, скорость сходимости процесса Ритца по числу параметров при использовании степенных полиномов не меньше, а в некоторых случаях больше, чем при других типах координатных функций.
При использовании большого количества параметров важное значение приобретают условия, которым следует подчинить координатные системы для того, чтобы решение алгебраической системы Ритца было устойчивым. Рост погрешности решения по сравнению с погрешностью коэффициентов уравнений является следствием малости определителя системы, которая в свою очередь есть следствие “почти” линейной зависимости координатных функций.
Во избежание неустойчивости решения системы линейных алгебраических уравнений относительно параметров по отношению к малым изменениям элементов матрицы и правой части системы (5.44), координатные функции желательно подчинить еще одному условию:
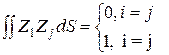. (5.49)
Под Z подразумеваются системы координатных функций.
Если координатные функции принадлежат к классу функций к конечной нормой по энергии, решение будет приближаться к точному, хотя эти функции могут и не удовлетворять статическим (естественным) условиям. Это является важным преимуществом метода Ритца по сравнению с другими методами.
При ортонормированных функциях получаемое решение значительно устойчивое к изменениям элементов матрицы, чем при степенных. Однако, если точность вычисления элементов матрицы и правой части настолько высока, что напряжения, рассчитываемые со всей возможной точностью в системе степенных функций (несмотря на плохие свойства порождаемой ею матрицы) несущественно отличаются от напряжений, вычисляемых при искажении матрицы и правой части, то пластины рассматриваемого типа можно рассчитывать с общими системами координатных функций.
При использовании ЭВМ основным требованием к системе координатных функций (кроме приведенных выше условий, вытекающих из теории энергетического метода) является минимальный расход машинного времени на вычисления значений этих функций и их производных, а также простота программирования.
Исходя из принятых граничных условий (5.47) и (5.48) в качестве координатных функций приняты степенные полиномы, коэффициенты которых приведены в таблицах 5.3-5.6.
Таблица 5.3
Коэффициенты полиномов fj (x), gj (y) для условий защемление-свободный край
| x2, y2 | x3, y3 | x4, y4 | x5, y5 | x6, y6 | x7, y7 | x8, y8 | x9, y9 | |
| f1, g1 | -3 | |||||||
| f2, g2 | -6 | |||||||
| f3, g3 | -10 | |||||||
| f4, g4 | -15 | |||||||
| f5, g5 | -21 | |||||||
| f6, g6 | -28 |
С другой стороны, если в нашем случае окажется, что сдвиг от поперечных сил в плоскостях xoz и yoz незначительно повлияет на напряжения изгиба s ix, s iy, то в дальнейшем для упрощения решения задачи в качестве координатных функций будут использованы степенные балочные функции, точно удовлетворяющие всем граничным условиям и получены, используя методы сопротивления материалов с началом расположения координатных осей в правом нижнем углу, т.е. для условий защемление- свободный край
f (k), g (k) = 1/24 (4 k - k 4 –3), (5.50)
Таблица 5.4
Коэффициенты полиномов lj (x), uj (y) для условий защемление-свободный край
| x1, y1 | x2, y2 | x3, y3 | x4, y4 | x5, y5 | x6, y6 | |
| l1, u1 | ||||||
| l2, u 2 | -1 | |||||
| l3, u 3 | -6 | |||||
| l4, u 4 | -1 | -30 | ||||
| l5, u 5 | -20 | -140 | ||||
| l6, u 6 | -1 | -210 | -630 |
Таблица 5.5
Коэффициенты полиномов fj (x), gj (y) для условий защемление-свободная опора
| x2, y2 | x3, y3 | x4, y4 | x5, y5 | x6, y6 | x7, y7 | x8, y8 | x9, y9 | |
| f1, g1 | -5 | |||||||
| f2, g2 | -12 | -43 | ||||||
| f3, g3 | -540 | -965 | ||||||
| f4, g4 | -9 | -6 | -5 | |||||
| f5, g5 | -40 | -27 | -43 | |||||
| f6, g6 | -276 | -3339 | -1400 | -965 |
Таблица 5.6
Коэффициенты полиномов lj (x), uj (y) для условий защемление-свободная опора
| x1, y1 | x2, y2 | x3, y3 | x4, y4 | x5, y5 | x6, y6 | x7, y7 | |
| l1, u 1 | -1 | ||||||
| l2, u 2 | -3 | ||||||
| l3, u 3 | -1 | -12 | |||||
| l4, u 4 | -13 | -50 | |||||
| l5, u 5 | -1 | -110 | -210 | ||||
| l6, u 6 | -31 | -770 | -882 |
для условий защемление-свободная опора
f (k), g (k) = 1/48 (3 k 3 – 2 k 4 – k), (5.51)
где в f (k) k принимает значение x, а в g (k) – y.
При этом в выражении (5.44) сj =0, а в (5.45) - для определения перерезывающих напряжений s ixz, s iyz cj заменяются на а 1; lj и uj - соответственно на f 1 и g 1, т.е. выражение для w o представляются в виде
w o (x,y) = a 1 f 1 (x) g 1 (y). (5.52)
Для определения жесткостных параметров слоев горных пород кровли, являющейся трансверсально изотропной средой, необходимо знать пять упругих параметров ее слоев: Еix, nix, Eixz, nixz, Gixz.
Остальные параметры определяются из общеизвестных соотношений
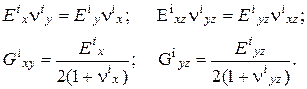(5.53)
Для трещиноватых массивов горных пород в зависимости от вида наиболее распространенных в шахтах трещин, учитывая, что трещины ориентированы преимущественно под углом 0 и 90о к оси z, приведенные упругие параметры определяются следующим образом.
Система зияющих трещин:
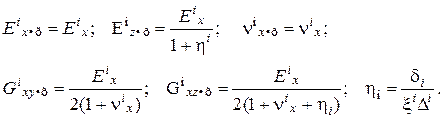(5.54)
где Eix пр – модуль упругости эквивалентной сплошной среды по направлению, совпадающему с поверхностью трещин; Eixz пр – модуль упругости эквивалентной сплошной среды по нормали к плоскости трещин; Gixy пр – модуль сдвига в плоскости изотропии, т.е. в плоскости xoy; Gixz пр – модуль сдвига в плоскости xoz; nixz пр – коэффициент Пуассона, определяемый как отношение поперечной деформации в плоскости xoz к продольной деформации в плоскости трещин; Eix; nix – модуль упругости и коэффициент Пуассона ненарушенного материала массива; D i – расстояние между трещинами; d i – ширина раскрытия трещины; x i – относительная площадь скальных контактов в данной трещине (x i = 3×10-4).
Система с хаотической трещиноватостью: для систем трещин примерно равной мощности и d i << hi расчет вели по формуле
(5.55)
где Ei 0 – приведенный модуль упругости; ni - число систем трещин;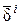 
– средняя ширина раскрытия трещин; 
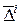– средняя протяженность ненарушенного материала, приходящегося на одну трещину.
Алгоритм решения задачи реализован как структурированный программный модуль, состоящий из нескольких блоков: присваивания начальных значений; определения расчетных величин; решения системы линейных алгебраических уравнений; определения напряжений; печати результатов в виде трехмерных и двумерных графиков.
Процедуры решения систем линейных алгебраических уравнений, дифференцирования и интегрирования функций реализованы в виде отдельных подпрограмм. Для решения системы линейных алгебраических уравнений, являющихся описанием математической модели, применен метод Гаусса с выбором главного элемента.
Определение численных значений интегралов осуществлено путем интерполирования подинтегральной функции кубическими сплайнами и дальнейшего применения квадратных формул. Дифференцирование функций реализовано с помощью метода Рунге-Кутта четвертого порядка. Алгоритм реализован с помощью пакета инженерного проектирования Maple V for Windows’95.
Исследования проводили в следующей последовательности, причем определяли:
- сходимость и устойчивость метода;
- влияние деформаций сдвига на напряжение от изгиба;
- адекватность метода сравнением результатов расчета с данными, имеющимися в литературе по пластинам прямоугольной формы, находящимся под действием равномерно распределенной нагрузки с подобными граничными условиями, а также проводили анализ изменения максимальных напряжений в зависимости от параметров плиты в плане с минимальной толщиной (жесткостью);
- зависимость максимальных напряжений от механических характеристик, жесткостных параметров, толщины, последовательности расположения слоев горных пород в кровле;
- максимальные напряжения в сечениях кровли; проводили сравнение их с предельными напряжениями и определяли направления и зоны разрушения пород.
На втором этапе была дана оценка напряженного состояния кровли горных пород с двумя наиболее характерными в практике системами трещин: зияющими и хаотическими с использованием механических характеристик по зависимостям (5.53) и (5.54).
Результаты исследований
Известно, что при увеличении количества параметров точность решения по методу Ритца должна возрастать. Чтобы установить минимальное количество параметров, необходимых для получения практически приемлемой точности, с помощью разработанного алгоритма, составленной программы на ПЭВМ, были проведены расчеты для кровли с двумя вышеуказанными граничными условиями
(см. рис. 5.1 в, г). В качестве координатных функций использованы системы степенных полиномов, коэффициенты которых приведены в вышеуказанных таблицах.
В связи с симметричностью граничных условий в направлениях x, y и одинаковыми размерами в плане, исследовали изменение максимальных нормальных s x, продольных s xy и поперечных s xz напряжений сдвига в нижней поверхности слоя угля с последовательностью расположения слоев горных пород и их механическими характеристиками согласно таблиц 5.1 и 5.2 при количестве параметров
n = 5, 7, 10, 14, 17.
Как показали результаты исследований, при переходе от одного варианта к другому до n =14 происходит уточнение напряжений, поэтому в расчетах использовано именно такое, т.е. n =14, число параметров.
Проведена численная проверка степени устойчивости решения системы Ритца - определение параметров и напряжений при использовании степенных полиномов путем сравнения характерных результатов расчета, полученных со всей возможной точностью и после замены последнего десятичного разряда в коэффициентах уравнений нулем. Оказалось, что погрешность искомых величин (в данном случае - напряжений) существенно больше, чем погрешность, вносимая в параметры, а тем более в коэффициенты уравнений. Отсюда следует, что при использовании степенных полиномов, точность подсчета коэффициентов уравнений Ритца должна быть значительно выше точности искомых величин. Однако в данном расчете, учитывая высокую степень точности подсчета коэффициентов, указанная потеря точности мало повлияла на окончательные результаты.
Сравнение результатов расчета для максимальных напряжений от изгиба s x, при учете деформаций сдвига (сj ¹0) и без их учета, т.е. при с j =0, показали, что максимальная относительная погрешность составляет не более 7 %. Следовательно, для рассматриваемой расчетной схемы кровли, состоящей из слоев с указанными в таблице 5.2 механическими характеристиками, можно пренебречь влиянием сдвига на напряжения от изгиба.
Адекватность любого метода расчета проверяется путем сравнения его результатов с данными экспериментальных исследований или сопоставлением с результатами, полученными другими расчетными способами.
Из обширной технической литературы по многослойным пластинам и оболочкам не известны конкретные результаты для моментов или напряжений с такими сложными граничными условиями, которые рассматриваются в принятой расчетной схеме для горных пород кровли. В литературе приведены табличные результаты расчета максимальных моментов (напряжений) как функций нагрузки q и f, параметр в плане В, для некоторых точек 
при решении дифференциального уравнения равновесия однослойной изотропной прямоугольной в плане пластины, находящейся под равномерно распределенной нагрузкой, два смежных края которой жестко закреплены, два других – свободно-опертые, причем дана зависимость этих величин от параметров в плане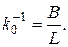 
Основным критерием для определения правильности использования балочных функций, а, следовательно, и метода решения, так как в данном случае применена известная и апробированная на практике техническая теория многослойных пластин с применением вариационного принципа, является сравнение качественной картины распределения максимальных напряжений, полученных по классическому и предложенному методам.
Анализ полученных результатов показал следующее. Максимальная относительная погрешность при расчете по разработанному методу в указанном интервале отношений сторон плиты составляет менее 10 %, причем в контрольных точках знаки совпадают, поэтому можно сделать вывод о правильности качественной картины распределения напряжений, а следовательно выборе балочных степенных функций в качестве координатных функций.
При равенстве сторон плиты, действии равномерно распределенной нагрузки и симметричных граничных условиях, напряжения в двух направлениях равны между собой, а с увеличением отношения сторон увеличиваются напряжения в направлении большей стороны и наоборот. Такая ситуация в реальных условиях наблюдается при отходе лавы от разрезной печи. При этом скорость изменения нормальных положительных (растягивающих) напряжений изгиба выше, чем поперечных сдвигающих отрицательных напряжений, возникающих в середине большей защемленной стороны, и значительно выше нормальных отрицательных (сжимающих) напряжений в этой же точке пластины (плиты).
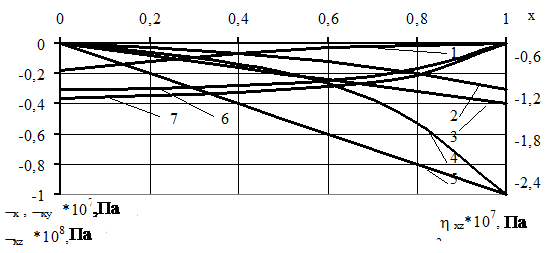
Распределение максимальных нормальных изгибающих, продольных и поперечных напряжений сдвига для квадратной плиты в направлении оси x, полученные в результате расчета по данному методу с указанными начальными данными, приведены на рис. 5.2 на основании которых и не приведенных здесь других результатов исследований в силу их громоздкости, составлена табл. 5.7 и сделаны вышеизложенные выводы.
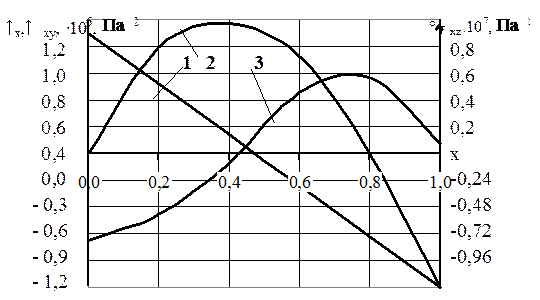
Рис. 5.2. Распределение максимальных напряжений в нижней поверхности слоя угля, оставленного в кровле, при t =6, k 0-1=1, для граничных условий типа «два смежных края защемлены, два других – свободно опертые»:
1 – s xz (x, ½); 2 – s x (x, ½); 3 – s xy (x,0)
Данные по сравнению отношений поперечных сдвиговых напряжений в табл. 5.7. отсутствуют, поскольку для тонкой пластины по классической теории они не приведены из-за их малости. В нашем случае максимальные их значения в восемь раз превышают соответствующие нормальные напряжения в точке (1, ½).
Таблица 5.7.
Зависимость отношений максимальных напряжений от параметров в плане для граничных условий защемление-свободная опора по классическому и
разработанному методам
| 
| 
| 
| ||
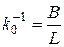
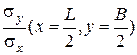
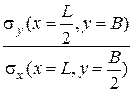
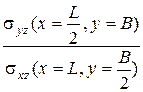
| классиче- ский метод | разработан- ный метод | классиче- ский метод | разработан- ный метод | разработанный метод | |
| 0,5 | 3,01 | 3,28 | 1,50 | 1,46 | 2,15 |
| 0,6 | 2,29 | 2,50 | 1,40 | 1,37 | 1,80 |
| 0,7 | 1,79 | 1,67 | 1,29 | 1,27 | 1,50 |
| 0,8 | 1,44 | 1,57 | 1,18 | 1,15 | 1,30 |
| 0,9 | 1,19 | 1,30 | 1,08 | 1,06 | 1,10 |
| 1,0 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 |
| 1,1 | 0,86 | 0,94 | 0,93 | 0,85 | 0,90 |
| 1,2 | 0,74 | 0,81 | 0,87 | 0,80 | 0,85 |
| 1,3 | 0,60 | 0,65 | 0,82 | 0,75 | 0,78 |
| 1,4 | 0,56 | 0,60 | 0,78 | 0,72 | 0,70 |
| 1,5 | 0,52 | 0,54 | 0,75 | 0,69 | 0,67 |
| 1,6 | 0,47 | 0,51 | 0,73 | 0,67 | 0,60 |
| 1,7 | 0,42 | 0,46 | 0,71 | 0,65 | 0,55 |
| 1,8 | 0,39 | 0,43 | 0,69 | 0,63 | 0,50 |
| 1,9 | 0,36 | 0,39 | 0,68 | 0,62 | 0,48 |
| 2,0 | 0,33 | 0,36 | 0,67 | 0,61 | 0,46 |
Аналогичные результаты для отношений максимальных напряжений плиты, возникающих в точках (x=L, y= 0); (x=L, у=В /2)с другими граничными условиями: два смежных края защемлены, два других - свободные, представлены в табл. 5.8, а распределение максимальных напряжений на рис. 5.3. Откуда следует, что в этом случае наибольшие нормальные и поперечные напряжения сдвига возникают в точках х =1, у =0 и х=1, у =1/2, а продольные напряжения сдвига - соответственно в точках х =0, у =0 и х =0; у =1/2 (см. рис. 5.3).
Таблица 5.8.
Зависимость отношений максимальных напряжений от параметров в плане
для граничных условий защемление-свободный край по разработанному методу
|
| 
| 
| 
| 
|
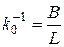
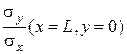
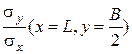
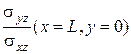
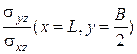
| 0,5 | 3,93 | 3,75 | 2,00 | 2,93 |
| 0,6 | 3,20 | 2,93 | 1,71 | 2,20 |
| 0,7 | 2,40 | 2,00 | 1,42 | 1,80 |
| 0,8 | 1,85 | 1,43 | 1,23 | 1,42 |
| 0,9 | 1,32 | 1,12 | 1,11 | 1,21 |
| 1,0 | 1,00 | 1,00 | 1,00 | 1,00 |
| 1,1 | 0,82 | 0,90 | 0,92 | 0,91 |
| 1,2 | 0,70 | 0,80 | 0,85 | 0,82 |
| 1,3 | 0,60 | 0,71 | 0,79 | 0,75 |
| 1,4 | 0,53 | 0,62 | 0,75 | 0,65 |
| 1,5 | 0,44 | 0,50 | 0,70 | 0,58 |
| 1,6 | 0,37 | 0,45 | 0,65 | 0,51 |
| 1,7 | 0,32 | 0,37 | 0,60 | 0,46 |
| 1,8 | 0,29 | 0,34 | 0,56 | 0,41 |
| 1,9 | 0,27 | 0,30 | 0,53 | 0,37 |
| 2,0 | 0,25 | 0,27 | 0,50 | 0,34 |
При этом наблюдается подобная тенденция, но с большей скоростью изменения напряжений по сравнению с предыдущими граничными условиями в зависимости от отношения сторон плиты (кровли), причем скорость изменения выше для нормальных напряжений изгиба в точке х=L, у =0, чем для тех же напряжений в точке x=L, у=В /2 и тем более для поперечных напряжений сдвига соответственно в точках х=L, у=В /2 и х= L, у =0.
Аналогичное распределение напряжений с практически равными значениями по величине, но с обратными знаками, наблюдается в верхней поверхности верхнего слоя плиты, т.е. при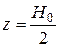 
, даже при значительной разнице модулей упругости этих слоев.
Последовательность расположения слоев горных пород кровли, их толщины и механические характеристики, как было отмечено выше, меняются в широких диапазонах, поэтому изучено влияние изменения этих параметров на ее напряженное состояние.
Рассмотрена одна из наиболее распространенных пожароопасных ситуаций, когда в кровле отрабатываемого пласта оставляют пачку угля. Получены распределения максимальных напряжений в нижнем слое толщи пород кровли пласта в зависимости от общей мощности (толщины) Н 0 кровли и отношения модулей упругости в плоскости напластования горных пород к поперечному их направлению при количестве слоев t =6 и отношении параметров в плане 
, результаты которых для двух видов граничных условий приведены на рис.5.3-5.6.
Рис.5.2. Распределение максимальных напряжений в нижней поверхности слоя угля, оставленного в кровле, при 
, для граничных условий: два смежных края защемлены, два других – свободные:
1– s x (x,0); 2 – s x (x, ½); 3 – s xz (x,1/2); 4 – s x (x,0); 5 – s xz (x,0);
6 – s xy (x,1/2); 7 – s xy (x,0)
Как показывают результаты исследований, в обоих случаях при увеличении толщины и отношения модулей упругости, напряжения уменьшаются, при этом, как и следовало ожидать, их величины значительно выше у плиты с граничными условиями защемление-свободный край.
Максимальные напряжения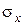 
и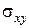 
для плиты с граничными условиями защемление-свободная опора не приведены, так как они ниже, чем предел прочности угля, следовательно анализу в дальнейшем не подлежат.
В ситуации с граничными условиями защемление-свободный край, при изменении отношения модулей упругости слоев в указанном интервале, плоское напряженное состояние плиты меняется незначительно, поэтому эти результаты также не приведены.
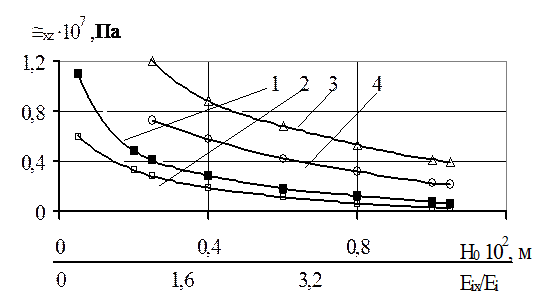
Рис. 5.3. Зависимость максимальных поперечных напряжений сдвига в слое угля от мощности кровли (1,2) и коэффициента анизотропии пород (3,4) при 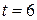, 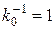для граничных условий:
два смежных края защемлены, два других – свободно опертые:
1,3 – s xz (1,1/2); 2,4 – s xz (0,1/2)
Рис.5.4. Зависимость максимальных напряжений s x , s xy в слое угля от его толщины при 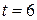, 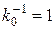для граничных условий:
два смежных края защемлены, два других – свободные:
1 – s x (0,1); 2 – s xy (0,1/2); 3 – s xy (0,0); 4 – s x (1,1/2); 5 – s x (1, 0)
 |
Рис. 5.5. Зависимость максимальных поперечных напряжений сдвига в слое угля от толщины (1,2) и коэффициента анизотропии (3.4) при 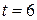, 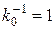для граничных условий: два смежных края защемлены, два других свободные: 1,3 – s xz (1,0); 2,4 – s xz (1,1/2)
Исследования влияния на напряженное состояние кровли в зависимости от расположения слоев (без слоя угля), их толщины, жесткости с различной комбинацией, общей жесткости проведено с использованием данных табл. 5.9, результаты которых для двух случаев граничных условий приведены на рис.5.7 и 5.8.
Отсюда следует, что независимо от указанных варьируемых параметров слоев, напряженное состояние кровли зависит от общей жесткости, причем, как и в предыдущих случаях, с увеличением жесткости (толщины) напряжения уменьшаются и наоборот, а скорость изменения напряжений значительно выше в точке (x =1, y =0) - в начале защемленного края при граничных условиях защемление-свободный край и в точке (x =1, y =1/2) для граничных условий защемление-свободная опора.
В результате тектонических процессов и воздействия очистных работ в горных породах образуются трещины, которые влияют на механические характеристики кровли, а, следовательно, на ее напряженное состояние. Используя данные табл. 5.9 зависимости, в том числе усредненные значения для ширины трещины и расстояния между трещинами, исследовано напряженное состояние плиты с
 Расстояние между трещи-нами,
Di, м
| 5×10-2 | 5×10-2 | 5×10-2 | 5×10-2 | ||||||
| Ши-рина тре-щи-ны, di, м | 10-4 | 10-4 | 10-4 | 10-4 | ||||||
| Жесткость (Па·м3,) на | сдвиг в попе- речном направл D*o, | 7,7 ×1011 | 6,1 ×1011 | 5,1 ×1011 | 2,7 ×1011 | |||||
| изгиб плиты, Do, | 4,0 ×1014 | 1,9 ×1014 | 1,1 ×1014 | 0,17 ×1014 | ||||||
| изгиб слоев, Di, | 1,6×1013 3,0×1012 1,9×1012 2,9×1011 | 2,4×1013 5,0×1012 5,0×1011 2,9×1010 | 3,6×1012 2,5×1012 5,0×1011 1,6×1012 | 2,9×1010 5,8×1010 4,0×1011 1,9×1012 | ||||||
| Общая тол-щина плиты Нo, м | ||||||||||
| Тол-щина слоев, hi, м | ||||||||||
| Последователь-ность расположения слоев кровли с параметрами в плане k-1o=1 | Песчаник Известняк Алевралит Аргиллит | Аргиллит Известняк Алевралит Песчаник | Аргиллит Алевралит Песчаник Известняк | Аргиллит Алевралит Песчаник Известняк | ||||||
| № пп | ||||||||||
наиболее распространенными их системами: зияющими и с хаотической трещиноватостью, основные результаты которых для двух видов граничных условий приведены на рис.5.9 и 5.10.
В связи с тем, что значения модулей деформаций меньше значений модулей упругости для сплошной среды, а, следовательно, снизится общая жесткость, то с увеличением толщины уменьшается напряженное состояние плиты, что подтверждают приведенные результаты. При этом уровень напряжений ниже у пород с хаотической трещиноватостью. Следует отметить, что напряжения в кровле с зияющими трещинами в направлении оси у значительно ниже (примерно на три порядка), чем в направлении оси х.
На основании приведенных выше результатов исследована прочность горных пород кровли, для чего проведено сравнение максимальных напряжений, возникающих в кровле с предельными их значениями для каждого слоя согласно табл.5.1, и, если они равны или их превышают, определены направления и зоны образования трещин.
Отправной точкой для этих исследований являются распределения напряжений в кровле с минимальной толщиной шести слоев, разными параметрами в плане и двумя случаями граничных условий, которые приведены на рис. 5.2 и 5.3.
Для кровли с граничными условиями защемление-свободная опора, распределение напряжений получено для слоя угля (см. рис. 5.2), а предельные их значения приведены в табл. 5.1. Из рис. 5.2 видно, что максимальные значения нормальных напряжений s х (1; 1/2) равные 1,5×105 Па, и продольные (касательные) напряжения сдвига s ху (0;0) - 0,97×105 Па ниже минимальных предельных их значений на растяжении и сдвиг для угля, меняющихся соответственно в пределах (2,5…22,5) 105 и (24…100) 105 Па (см. табл. 5.1).
 |
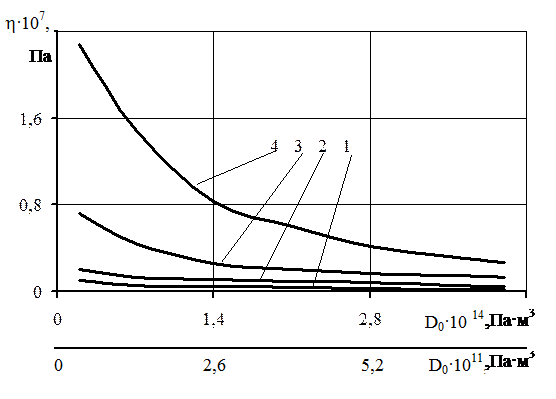Рис.5.6. Зависимость максимальных напряжений s x, s xz от общей жесткости на изгиб D 0 и s xz от жесткости на сдвиг 
в слоях кровли при 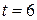, 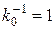для граничных условий: два смежных края защемлены, два других – свободно оперты: 1 – 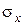(1/2,1/2); 2 – s x (1,1/2); 3 – 
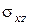(0,1/2);
4 - 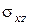(1,1/2)
В тоже время поперечные (касательные) напряжения сдвига
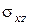(1;1/2)=1,2·105 Па, то есть посередине защемленного края, превышают предельные их значения на всем интервале, а 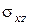(0;1/2) = 0,72·105 Па, посередине опертого края, равно или превышает эти значения на интервале (24…72)·105 Па. При этом разрушающие напряжения могут возникнуть на расстоянии (1…0,5),
30 м от защемленного края и соответственно (0…0,25), т.е. 15 м от опертого края.
Таким образом, в участке кровли, с одинаковыми параметрами в плане
(
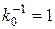), состоящей из шести слоев одинаковой минимальной толщины с параметрами согласно табл. 5.1 и 5.2 при условиях крепления защемление-свободная опора могут возникнуть в направлениях xoz и yoz трещины посередине защемленных и опертых краев, причем в первом случае на расстоянии примерно в два раза больше, чем во втором.
 |
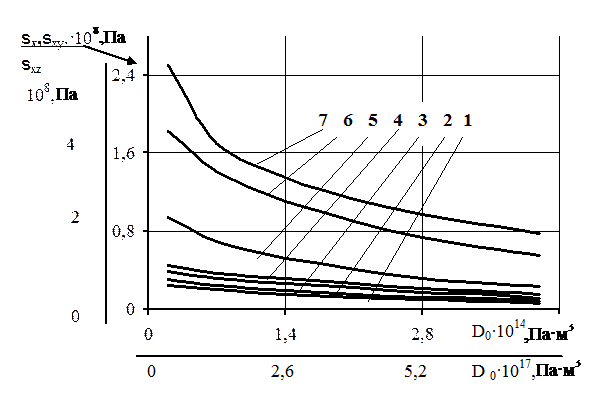Рис. 5.7. Зависимость максимальных напряжений 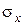, 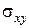от общей жесткости на изгиб 
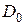и 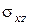от жесткости на сдвиг в слоях кровли при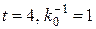 
для граничных условий два смежных края защемлены, два других – свободны: 1 - 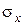(0,1); 2 – 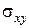(0,1/2); 3 – 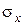(1,1/2); 4 - 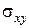(1,1/2);
5 – 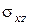(1,1/2); 6 – 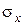(1,0); 7 – 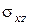(1,0)
С увеличением толщины кровли и отношения модулей упругости ее напряженное состояние снижается (см. рис. 5.4) и при Н о>30 м,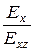 
>4,0 в середине опертого края, если 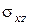предельное равно 24×105 Па, а Н о>8 м, 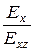>1,4 в середине защемленного края, если 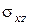предельное равно 100×105 Па, или Н о>50 м, если s xz предельное равно 24×105 Па, трещины образовываться не будут.
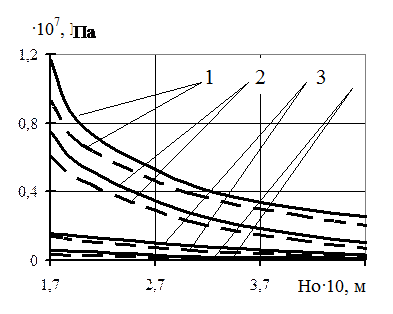
Рис. 5.8. Зависимость максимальных напряжений в слоях кровли с системами трещин (d i =10-4 м, D i =5 10-2 м) при 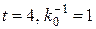для граничных условий два смежных края защемлены, два других – свободно опертые:
1 – s x (1/2,1/2); 2 – 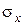(1,1/2); 3 – 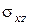(0,1/2); 4 - 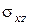(0,1/2); 5 – 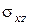(1,1/2);
6 – s x (1,0);
трещины: зияющие – 
хаотические – 
Если плита состоит из четырех слоев различной жесткости (см. табл. 5.5), то, как следует из рис. 5.7, ее напряженное состояние снижается с увеличением жесткостей на изгиб и поперечный сдвиг. В этом случае нормальные s x (1;1/2),
s х (1/2;1/2) и поперечные напряжения сдвига s хz (0;1/2) значительно ниже их предельных значений для указанных пород и только напряжения поперечного сдвига s хz (1;1/2), т.е. в середине защемленного края, близки к минимальному предельному значению напряжения для алевролита и превышают соответствующие их значения для аргиллита, песчаника (крупнозернистого) и известняка при 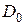=0,17×1014 Па и =0,3×1011 Па, что говорит о возможности появления аналогичных трещин в середине защемленных краев от поперечных сил.
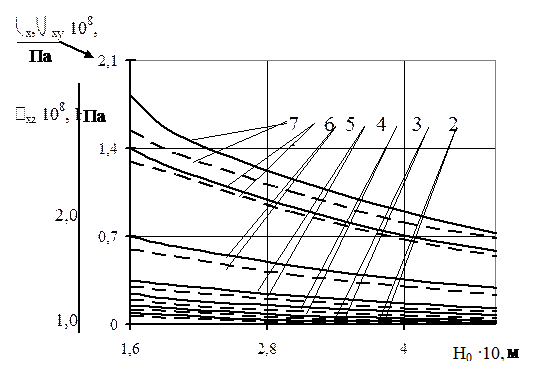
Рис. 5.9. Зависимость максимальных напряжений в слоях кровли с системами трещин (d i =10-4 м, D i =5 10-2 м) при 
от толщины плиты для граничных условий два смежных края защемлены, два других – свободные: 1 – s x (0, 1); 2 – s xy (0,1/2); 3 – s x (1,1/2); 4 - s xy (0,0);
5 – s xz (1,1/2); 6 – s x (1,0); 7– s xz (1,0);
трещины: зияющие - ; хаотические -
Выше рассматривалось напряженное состояние кровли с одинаковыми параметрами в плане, т.е. при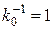 
. Однако распределение напряжений меняется в зависимости от их отношения (см. табл.5.5), причем напряжения увеличиваются в направлении большей стороны и при 
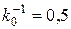или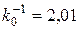 
нормальные напряжения в одном из направлений больше примерно в 1,5 и 3,0 раза, а поперечные напряжения сдвига примерно в 2,0 раза. Поэтому в данном случае максимальные нормальные напряжения в точке (1/2;1/2), т.е. вблизи середины плиты достигнут предельного их значения для угля и могут появиться трещины в направлении большей стороны, соответствующие напряжения в середине защемленного края (1;1/2) приблизятся к предельному значению, а увеличение поперечных напряжений сдвига повлечет за собой увеличение зоны появления трещин.
В кровле с четырьмя слоями нормальные напряжения в этих двух точках достигнут предельных значений на растяжение только для алевролита, что явится причиной появления здесь трещин, а поперечные напряжения сдвига, увеличенные в 2,15 раза в середине защемленного края, вызовут появление трещин также у алевролита и песчаника (мелкозернистого). При этом расширится область появления трещин с увеличением значений жесткостей (толщины) и отношения модулей упругости слоев кровли.
Перейдем к исследованию прочности кровли с граничными условиями защемление - свободный край, для чего, как и в предыдущем случае, рассмотрим распределение напряжений, приведенное на рис.5.3.
В данном случае напряженное состояние плиты естественно значительно выше, а опасными точками, подлежащими анализу для определения ее прочности, являются: для нормальных напряжений s x (1, 0), s x (1,1/2), s x (0,1), для продольных напряжений s xy (0, 0), s xy (0,1/2) и поперечных напряжений s xz (1, 0) и s xz (1,1/2). Аналогичная картина распределения напряжений наблюдается в направлении оси y с координатами при замене х на y, и наоборот.
Как следует из рис. 5.3 наиболее нагруженными точками, откуда начнут появляться во всех направлениях трещины являются места начального защемления краев кровли, где возникают нормальные s x, s y и поперечные s xz, s yz напряжения сдвига, которые, несмотря на снижение их к свободным краям, на большей части интервала длины превышают соответствующие предельные значения для угля на растяжение, сжатие и сдвиг. Разрушающими являются эти напряжения в средней части защемленных краев, которые, будучи меньше примерно в три раза с аналогичным законом изменения к свободным краям, также на большом своем интервале превышают продольные значения. Разрушающими для слоя угля являются и продольные напряжения сдвига, которые, незначительно отличаясь по величине в уступе в средней части свободных краев плиты и уменьшаясь к защемленным ее краям, могут явиться причиной появления зияющих трещин. Несмотря на то, что с увеличением отношения модулей упругости слоев пород и их толщин напряженное состояние кровли снижается (см. рис. 5.5, 5.6), в указанных точках во всех направлениях трещины сохранятся.
В четырехслойной кровле с различным расположением слоев при увеличении их жесткостей (толщин) в пределах, указанных в табл.5.5 и рис.5.8, несмотря на снижение напряженного состояния, во всех этих точках действуют те или иные разрушающие напряжения или их сочетания, которые обуславливают появление систем с хаотической трещиноватостью.
С изменением параметров в плане напряжения в плите значительно возрастут (см. табл. 5.8) в направлении большей защемленной стороны.
Более подробно исследовать зоны появления трещин нет необходимости, т.к. при рассматриваемых граничных условиях во всех приведенных выше случаях произойдет обрушение кровли.
Таким образом, разработанный метод позволяет исследовать напряженное состояние кровли горных пород, состоящей из различного сочетания слоев переменной жесткости под действием распределенной нагрузки от собственной массы при различных граничных условиях, а, следовательно, определять напряжения, зоны образования, вид трещин и влияние изменения горно-геологических условий на изменение газодинамического режима проветривания горных выработок.
