ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ В ГЕОМЕХАНИКЕ
Общие сведения
Массивы горных пород (горная выработка, кровля, целик, ствол и т.д.) являются трехмерными системами, состоящие из слоев анизотропных пород, которые могут иметь переменные толщину, внешнюю нагрузку и различные граничные условия.
Оценим возможность применения некоторых известных методов к исследованию их напряженно-деформируемого состояния как многослойных толстых пластин (плит) с учетом поперечного сдвига (влиянием поперечных сил).
Тот факт, что на одних краях массива горных пород (плиты) заданы перемещения, а на других усилия, делает задачу смешанной. Задачи об изгибе плиты со смешанными условиями опирания сложнее обычных, поэтому, в обширной литературе о пластинах (оболочках) имеется сравнительно мало работ, посвященных изгибу даже обычных однослойных пластин (оболочек) со смешанными краевыми условиями.
В общем случае, когда жесткость – функция координат и отсутствует свободное опирание на противоположных краях, сложность дифференциальных разрешающих уравнений и граничных условий, приведенных в разделе 2, вынуждает применять приближенные методы.
Одним из широко используемых численных методов решения краевых задач является метод сеток, который приведен выше и, несмотря на простоту и возможность применения его к пластинам (оболочкам) с произвольной толщиной при любых условиях крепления и нагрузке, фактически в таких задачах используется редко, так как дифференциальное уравнение равновесия имеет переменные коэффициенты и шаг сетки должен быть меньше, чем при постоянных толщине и нагрузке, а тем более при учете анизотропности слоев и поперечного сдвига, то значительно увеличивается количество подлежащих составлению и решению алгебраических уравнений. Матрица системы получается плохо обусловленной, большой по объему, имеет мало отличных от нуля элементов, составление программы усложняется формулами, вытекающими из краевых условий.
По методу прямых конечностными разностями заменяют частные производные только по одному направлению. При этом получают систему дифференциальных уравнений в обыкновенных производных, общее решение которых можно найти для некоторых частных случаев переменных толщин, нагрузки, слоистости и анизотропии горных пород. Получить точное решение системы дифференциальных уравнений методом прямых можно только при изменении толщины и нагрузки по простым законам с учетом только изотропии слоев. В общем случае это сделать не удается, поэтому для отыскания решения необходимо использовать один из численных методов интегрирования. Кроме того, недостатком метода прямых является необходимость составления и решения алгебраических уравнений для удовлетворения краевым условиям на противоположных краях пластины (оболочки) при любых способах их закрепления.
Приведенная краткая характеристика конечноразностных методов показывает, что применение их для расчета массивов горных пород, в принципе возможно, но толъко для решения плоских задач. Это относится и к методу конечных элементов.
По методу коллокаций прогибы пластины (оболочки, представляются в виде конечного ряда заданных функций, умноженных на параметры. Для вычисления параметров строится система алгебраических уравнений из условий, что уравнения и граничные условия удовлетворяются в ряде точек пластины (оболочки). Метод коллокаций дает хорошие результаты, если заданные функции удовлетворяют уравнению равновесия и граничным условиям. В общем случае такие функции подобрать трудно.
Для расчета пластин и оболочек широко применяют вариационные методы теории упругости.
Известно, что основные проблемы механики наряду с дифференциальными уравнениями управляются так называемыми минимальными принципами. Так, например, положение равновесия механической системы есть положение, отвечающее минимуму ее потенциальной энергии. Ввиду этого проблема решения граничной задачи для дифференциального уравнения данной механической системы оказывается, в общем, эквивалентной проблеме нахождения функции, дающей минимум интеграла, которым выражается потенциальная энергия системы.
Для решения задач об изгибе пластин (оболочек) можно использовать вариационный принцип Рейсснера, при котором одновременно отыскивается прогиб и все моменты, представляющие также как и прогиб, в виде конечных сумм произведений неопределенных параметров на заданные координатные функции, которые выбирают так, чтобы они были равны нулю на свободных краях пластины (оболочки). Расчетные формулы и машинный алгоритм принципа Рейсснера очень сложный.
Расчет пластин (оболочек) по методу Бубнова-Галеркина значительно усложняется, так как необходимо удовлетворять координатными функциями все граничные условия, в том числе и условия на свободных краях. Последнее обстоятельство препятствует использование на практике метода Треффца и метода наименьших квадратов. Однако если эти условия выполняются, то эти методы весьма эффективны в применении. Можно утверждать, что ввиду сложности задач о напряженно-деформируемом состоянии массивов горных пород, любой метод исследования, обеспечивающий необходимую точность, потребует весьма громоздких вычислений. Поэтому, естественно, следует применять такой метод, который просто реализуется на ПЭВМ и позволяет получить решение, не прибегая к дополнительным (по сравнению с обычной теорией пластин и оболочек) приближенным допущениям.
Для решения краевых задач горной геомеханики является эффективным применение метода Ритца – одного из основных прямых методов вариационного исчисления.
Метод (процесс) Ритца является одним из методов построения минимизирующей последовательности. Для упрощения выкладок ограничимся случаем вещественного гильбертова пространства 
; результаты переносятся на комплексное пространство без изменений.
Пусть 
– положительно определенный оператор в пространстве . Задача о построении обобщенного решения уравнения
(5.1)
равносильна задаче о построении элемента энергетического пространства, который реализует минимум функционала
(5.2)
в энергетическом пространстве. Эту последнюю задачу будем приближенно решать следующим образом.
Выберем последовательность элементов
(5.3)
удовлетворяющих следующим трем условиям:
1) все элементы 
2) при любом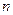 
элементы 
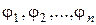линейно независимы;
3) последовательность (5.3) полна в 
.
Элементы (5.3), следуя Ритцу будем называть координатными. Совокупность координатных элементов назовем координатной системой.
Построим линейную комбинацию первых 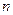координатных элементов
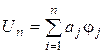(5.4)
с произвольными численными коэффициентами 
. Подставим 
вместо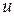 
в функционал (5.2); это превратит 
в функцию 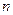независимых переменных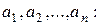 
(5.5)
Выберем коэффициенты так, чтобы функция (5.5) приняла минимальное значение. Как увидим, это приводит к системе линейных алгебраических уравнений с неизвестными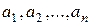 
. Функция (5.5) достигает минимума при тех значениях независимых переменных, которые обращают в нуль ее первые производные:
(5.6)
Производные (5.6) легко вычисляются:
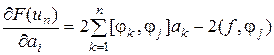(5.7)
Приравняв эти производные нулю, получим систему Ритца
(5.8)
или в более подробной записи,
|
……………………………………………………..
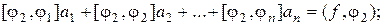
Координатные элементы (5.3) можно выбрать из области 
; тогда 
, и система Ритца принимает вид (
– область определения оператора )
|
………………….………………………………………..
.
определитель системы (5.9)
(5.10)
есть определитель системы Грамма линейно независимых элементов 
и поэтому отличен от нуля. Отсюда следует, что система уравнений Ритца всегда разрешима, если оператор 
положительный. Найдя коэффициенты 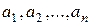и подставив их в (5.4), получим элемент 
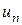, который будем называть приближенным решением уравнения (5.1) по Ритцу. Зная прогибы, определим деформации и напряжения.
Теорема. Если – оператор положительно определенный, то приближенные по Ритцу решения уравнения (5.1) сходятся к точному обобщенному решению этого уравнения как по энергии, так и в метрике исходного пространства.
Легко видеть, что последовательность приближенных решений по Ритцу – минимизирующая для функционала энергии.
Приближенное по Ритцу решение 
тем ближе (в смысле близости по энергии) к точному, чем больше 
. Для достижения высокой точности приходиться брать большое , т.е. большое число координатных функций. Это приводит к необходимости решать систему (5.9) с большим числом уравнений и неизвестных. Отметим только, что решение системы (5.9) облегчается ее симметричностью.
Замечание 1. Если система (5.9) уже построена и по тем или иным причинам желательно получить менее точное приближение, не содержащее некоторых из координатных функций, то коэффициенты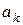 
, соответствующие этому менее точному приближению, найдутся из системы, которая получается из системы (5.9) усечением, т.е. вычеркиванием строк и столбцов, соответствующих отброшенным координатным функциям.
Замечание 2. Требование полноты координатной системы не вполне необходимо. Действительно, нет необходимости в том, чтобы любой элемент энергетического пространства можно было аппроксимировать координатными элементами – достаточно, чтобы такую аппроксимацию допускало обобщенное решение. Поэтому, если заранее известно, что искомое решение принадлежит к некоторому классу, более узкому, чем 
, то достаточно, чтобы координатная система была полна в этом классе. Например, если известно, что искомая функция четная относительно какого-либо из независимых переменных, то можно брать в качестве координатных только четные функции той же переменной, и достаточно, чтобы выбранная система координатных функций была полной относительно четных функций из .
Метод Ритца имеет простую схему расчета и позволяет исследовать массивы горных пород с любым сочетанием слоев при любой нагрузке и условиях закрепления, различной анизотропией пород. Для решения многих важных для практики задач достаточно, в отличие от метода Бубнова – Галеркина, чтобы координатные функции удовлетворяли только геометрическим граничным условиям, записываемых относительно функции прогиба и ее производной (угла поворота).
Приведем решения некоторых задач о напряженно-деформированном состоянии массивов горных пород, используя вариационный метод исчисления.
Влияние напряженно-деформированного состояния пород кровли пласта на образование пожароопасных зон
Из-за резкого сокращения объемов строительства новых горизонтов, панелей и блоков на шахтах дорабатывают выемочные поля со сложными и неоднородными геологическими условиями. В пределах одного поля наблюдается изменение мощности пласта или вмещающих его пород, их физико-механических свойств, исчезновение отдельных слоев и тому подобное.
До недавнего времени отсутствовали способы учета влияния изменений геологических условий при прогнозировании эндогенной пожароопасности горных выработок. Раскрытие этих проблемных вопросов представляется возможным при условии определения параметров напряжений и деформаций в угленосном массиве, вмещающем горную выработку. Существенной значимостью является оценка влияния геологических (мощность слагающих кровлю пласта слоев, порядок их чередования, анизотропия механических свойств) и технологических (способ управления кровлей) условий разработки пласта на формирование самонагревающейся пожароопасной среды, а также учет этих факторов при разработке технологии профилактики эндогенных пожаров.
Современное состояние научных знаний о напряженном состоянии вмещающего очистную выработку горного массива во многом предопределено работами Ардашева К.А., Амусина Б.З, Борисова А.А., Бурчакова А.С., Глуш-
ко В.Т., Грядущего Б.А., Жукова В.В., Зборщика М.П., Зорина А.Н., Карто-
зия Б.А., Колоколова О.В., Либермана Ю.М., Назимко В.В., Руппенейта К.В., Черняка И.Л., Шемякина Е.И. и др.
Известны исследования, посвященные расчету напряженно-деформированного состояния пород вблизи очистных выработок, где породный массив рассмотрен как пластина с постоянной жесткостью и однородными граничными условиями под действием равномерно распределенной нагрузки, а решение дифференциального уравнения выполнено методом сеток. Принятые при этом граничные условия и допущения не адекватны условиям формирования параметров полостей в реальных условиях, приведенных в предшествующей главе.
Другие математические модели были разработаны для расчета крепей очистных выработок, их реализация сводилась к определению действующих на крепь усилий (напряжений) и сопутствующих им деформаций. Они не описывают напряженно-деформированного состояния пород кровли пласта, находящихся в выработанном пространстве. Как правило, в этих моделях рассмотрена плоская задача, характерная для наиболее нагруженного нормальными усилиями среднего участка лавы. Краевые части, где нагрузка распределена как на призабойную, так и околоштрековую области, этим моделям не соответствуют. Поэтому в целях прогнозирования параметров пожароопасных зон (полостей) возникла необходимость разработки соответствующей математической модели.
