Перемещения точек срединной поверхности в направлениях x, y, z обозначим соответственно через u, v, w. Для решения задачи используем прием, который предложил Тимошенко С.П., состоящий в представлении полного прогиба в виде суммы двух составляющих - за счет изгиба wo и сдвига w1:
w = w o + w 1. (5.11)
Физически такое представление w соответствует деформированию плиты в два этапа. В первом - деформации происходят, как и для обычной плиты без учета влияния сдвига на напряжения изгиба. Второй этап состоит в учете дополнительной деформации за счет сдвига.
Таким образом, специфической особенностью расчета слоистой плиты является учет влияния сдвига на величину изгибающих моментов, энергии сдвига от поперечных сил и определение ее механических характеристик при учете трещиноватости.
Деформации в любой точке i -го слоя (i =1,2...) плиты в предположении гипотезы прямых нормалей имеют вид
(5.12)
Деформации срединной поверхности
(5.13)
Параметры изменения кривизны в пределах точности технической теории
(5.14)
где 
– дополнительные слагаемые, учитывающие влияние перерезывающих сил.
Закон Гука для i -го слоя плиты записывается следующим образом
(5.15)
Решая систему уравнений (5.15) относительно компонент тензора напряжений и учитывая соотношения (5.12), получим
(5.16)
(5.17)
Интегрируя (5.16) по толщине каждого слоя и суммируя выражения по числу слоев, получим выражение для внутренних усилий в срединной поверхности
(5.18)
Умножая (5.16) на z и интегрируя, получим изгибающие и крутящий моменты
(5.19)
Решая соотношения (5.18) относительно компонент деформаций, имеем
(5.20)
В соотношениях (5.18-5.20) введены следующие обозначения
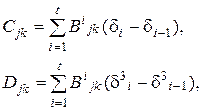(5.21)
где d i -1 – расстояние по нормали от внутренней поверхности до наружной поверхности i -го слоя;
, 
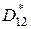– получены из (5.21) заменой Вij к на 
;
t - количество слоев.
(5.22)
Работа поперечных сил для элемента плиты
(5.23)
Для определения угла наклона касательной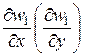 
использовано допущение, что высота плиты после деформации не изменится и равна ее высоте до деформации. Из этого следует, что угол наклона касательной численно равен углу сдвига плиты и постоянен по ее высоте. В силу постоянства угла сдвига будет постоянным и напряжение сдвига по высоте плиты. Поэтому согласно закону Гука
, (5.24)
где Q xz, Q yz - полные перерезывающие силы для плиты в целом;
G xz, G yz, H - модули сдвига по нормали и толщина плиты.
Потенциальная энергия элементарной площадки плиты от поперечных сил равна
(5.25)
Вариационное уравнение
В соответствии с принципом возможных перемещений вариация полной энергии деформированной плиты равна нулю в состоянии равновесия
, (5.26)
где d U – вариация потенциальной энергии плиты; d V – вариация потенциала внешних сил.
Вариация потенциальной энергии внешних сил
(5.27)
Интегралы в выражении (5.27) и ниже вычисляются в пределах 0£ x £ L,
0£ y £ В.
Вариация потенциальной энергии плиты может быть представлена как сумма вариаций энергий деформаций растяжения (сжатия) δ U р, деформации изгиба δ U и и деформации сдвига δ U с
(5.28)
где
, (5.29)
, (5.30)
. (5.31)
Здесь e xz, e yz – деформации сдвига в плоскости xoz и yoz соответственно.
Интеграл (5.29) представим в виде
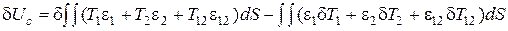. (5.32)
Такая запись d U c ведет к вариационному уравнению смешанного типа, в котором варьируются не только деформации, как в выражении (5.29), но и усилия в срединной поверхности.
Подставляя деформации в срединной поверхности по формулам (5.13) и интегрируя по частям, преобразуем выражение
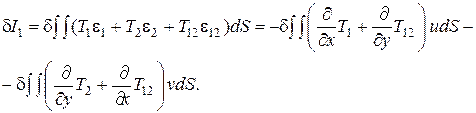(5.33)
Контурные интегралы в данном случае равны нулю, т.к. на закрепленном крае плиты перемещения равны нулю, а на свободно-опертом или свободном краях равны нулю усилия в срединной поверхности.
Введем функцию усилий j в срединной поверхности с помощью соотношений
. (5.34)
Здесь использованы краткие обозначения вторых производных в прямоугольных координатах.
Подставим выражение (5.34) в (5.33). Тогда первый и второй интегралы равны нулю, а следовательно d I 1 = 0.
Второй интеграл (5.32) с учетом зависимостей (5.20) имеет вид
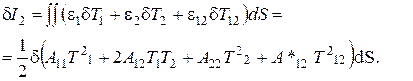(5.35)
Преобразуем интеграл (5.30), используя соотношения (5.19)
. (5.36)
Учитывая соотношения (5.35), (5.36), (5.31), (5.24), (5.27) и заменяя усилия в срединной поверхности их выражениями через функцию усилий по формулам (5.34), а параметры изменения кривизны - функциями прогибов w 0, w 1 из выражения (5.14), для вариации полной энергии слоистой плиты получим
(5.37)
Здесь введены следующие обозначения
(5.38)
В выражении L p(y,h) pjk принимает значения a jk,c jk, а функции y и h соответствуют функциям w и j.
Полученное вариационное уравнение (5.37) смешанного типа относительно прогибов и функции усилий для слоистой плиты имеет ряд преимуществ по сравнению с вариационным уравнением относительно перемещений, а именно:
– функция усилий (следует отметить, что ее удается ввести только в технической теории пластин) является независимо варьируемой, поэтому отпадает необходимость решать предварительно сложную задачу интегрирования уравнения совместности для того, чтобы выразить j через w 0;
– при наличии усилий в срединной поверхности разыскиваются три функции (w 0, w 1, j) вместо пяти (u a , v a, u b, v b, w);
– при любом выборе координатных функций для функции усилий уравнения равновесия в срединной поверхности удовлетворяются автоматически, что увеличивает точность решения;
– методы решения вариационных уравнений смешанного типа удобны для алгоритмизации, программирования и точной автоматизации счета на ЭВМ.
Из вариации уравнения (5.37) следует, что главными краевыми условиями для функций w 0, w 1 является
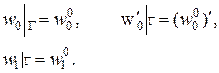(5.39)
где 
, ()¢, 
– заданные функции;
Г - контур срединной поверхности.
Главными краевыми условиями для функции усилий j, если край пластины свободен или свободно-опертый, является
(5.40)
Естественные краевые условия имеют сравнительно сложный характер, однако использование вариационного метода решения Ритца позволяет заранее не подчинять этим условиям координатные функции. Разумеется, если появляется возможность подчинить координатную систему всем краевым условиям, то это будет способствовать ускорению сходимости решения.
