теңдеуінің жалпы шешімін табу керек, мұндағыai, b – (х1, …, xn, u) белгілі функциялары. Ол үшін алдымен:
1) сипаттауыштар теңдеулер жүйесінің алғашқы интегралдарын табу керек
(*)
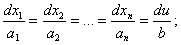2) берілген дербес туындылы теңдеудің жалпы шешімі болатын алғашқы интегралдардан қандай да бір F(j1, j2, …jn) функциясын құрастырамыз (jI – тәуелсіз, i = 1, …, n).
Бірінші ретті дербес туындылы теңдеудің Коши есебі дегеніміз: (*) теңдеуінің (n – 1) -өлшемді S бетінде
S = {r(S): x1(S1, …, Sn-1), x2(S1, …, Sn-1), …, xn(S1, …, Sn-1)}
u/S = w(S1, S2, …, Sn-1) шартын қанағаттандыратын u(x1, …, xn) шешімін табу есебі.
Мысал 1. Теңдеудің жалпы шешімін тап:
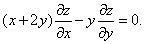
Шешуі. Сипаттауыштар теңдеулер жүйесін құрастырып, оны шешеміз:
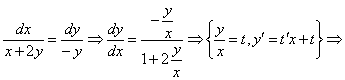
Алғашқы интеграл табылды: С1 = ху + у2.
Z = F(xy+y2) - функциясы теңдеудің жалпы шешімі болады, мұндағы F – кез келген дифференциалданатын функция.
Мысал 2.Теңдеуді шеш: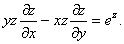 
Шешуі. Сипаттауыштар теңдеулер жүйесін құрастырайық:
Алғашқы бөлшектер жұбы алғашқы интегралды береді: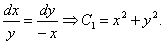 
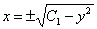-ді екінші бөлшектер жұбына қоямыз, сонда:
Соңғы теңдеуді интегралдай отырып, екінші алғашқы интегралды аламыз:
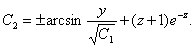
Сонда жалпы шешім:
Мысал 3.Теңдеуді шеш: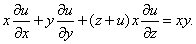 
Шешуі. Сипаттауыштар теңдеулер жүйесін құрастырып, оны шешеміз:
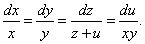
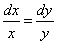теңдеуінен алғашқы интегралды аламыз: 
.
бөлшектеріне тең бөлшектерді түрлендіру ережесін қолданайық:
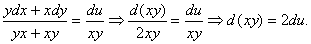
Бұдан екінші алғашқы интегралды аламыз: С2 = (½)ху - u.
және 
өрнектерін 
теңдеуіне қоямыз. Сонда:
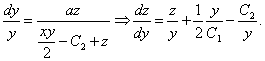
Алынған сызықтық теңдеуді шешеміз:
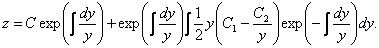
Үшінші алғашқы интегралды аламыз: 
Мысал 4. Коши есебін шеш:
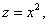y = 1.
Шешуі. Екі алғашқы интегралды табайық. Жүйе құрастырамыз:
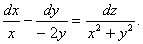
Бұдан бірінші алғашқы интегралды табамыз: С1 = х2у.
екенін ескере отырып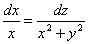 
теңдеуін шешсек, екінші алғашқы интегралды аламыз:
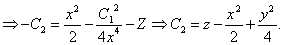
Екі алғашқы интегралға z = x2, y = 1 қоямыз:
Бұл теңдеулер жұбынан х-ті жойсақ, алғашқы интегралдарды байланыстыратын келесі теңдеуді аламыз: 
С1 және С2 орнына алғашқы интегралдарды қойсақ, Коши есебінің шешімін аламыз:
Мысал 5. Коши есебін шеш:
u = x2 + y2, z = 0.
Шешуі.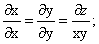 
- сипаттауыштар теңдеулер жүйесінің алғашқы интегралдарын табамыз: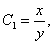 
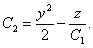
Бастапқы шарттарды пайдалана отырып алғашқы интегралдарды байланыстыратын келесі теңдеулерді аламыз:
u = x2 + y2 Þ u = 2C2(C12 + 1).
С1 және С2 алғашқы интегралдарды қойсақ, Коши есебінің шешімін аламыз:
Тест сұрақтары
$$$1Бірінші ретті дифференциалдық теңдеу?
A)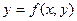 
;
B) 
;
C) 
;
D) 
;
E)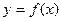 
;
$$$2Теңдеуді шешіңіз: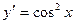 
.
A)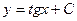 
;
B) 
;
C) 
;
D)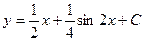 
;
E) 
;
$$$3 Теңдеуді шешіңіз: 
.
A) ;
B) 
;
C)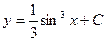 
;
D) 
;
E)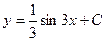 
;
$$$4Диф.теңдеудің жалпы шешімі?
A)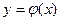 
;
B) ;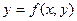
C)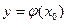 
;
D)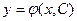 
;
E)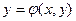 
;
$$$5Диф.теңдеудің дербес шешімі?
A) ;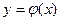
B) ;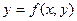
C) 
;
D) 
;
E) 
;
$$$6 Теңдеуді шешіңіз: 
.
A) 
;
B)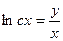 
;
C) 
;
D)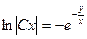 
;
E)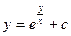 
;
$$$7 Теңдеуді шешіңіз: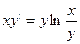 
.
A)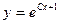 
;
B)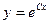 
;
C) 
;
D) 
;
E)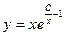 
;
$$$8Белгісізі айырылған диф.теңдеу?
A)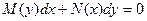 
;
B) 
;
C) 
;
D)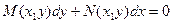 
;
E)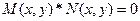 
;
$$$9Белгісізі айырылатын диф.теңдеу?
A)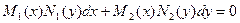 
;
B)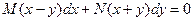 
;
C) 
;
D) 
;
E) ;
$$$10 Теңдеуді шешіңіз: 
.
A)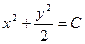 
;
B)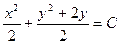 
;
C)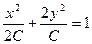 
;
D) 
;
E)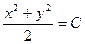 
;
$$$11 Теңдеуді шешіңіз: 
.
A)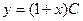 
;
B) 
;
C)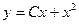 
;
D)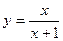 
;
E) 
;
$$$12 Біртекті диф.теңдеу?
A) ;
B)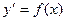 
;
C) 
;
D) 
;
E) 
;
$$$13 Біртектіге келтірілетін диф.теңдеу?
A)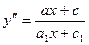 
;
B) 
;
C) 
D)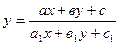 
E)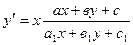 
$$$14 Теңдеуді шешіңіз: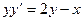 
.
A) 
;
B)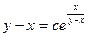 
;
C) 
;
D)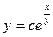 
;
E)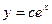 
;
$$$15 Теңдеуді шешіңіз: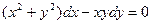 
.
A)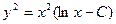 
;
B)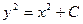 
;
C) 
;
D)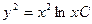 
;
E) ;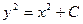
$$$16 Бернулли теңдеуі?
A)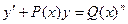 
;
B) 
;
C)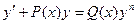 
;
D) 
;
E)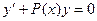 
;
$$$17 Теңдеуді шешіңіз: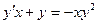 
.
A)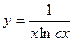 
;
B)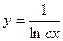 
;
C) 
;
D) 
;
E)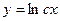 
;
$$$18 Диф.теңдеудің толық дифференциалдық болуының шарты?
A)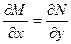 
;
B) 
;
C) 
;
D) 
;
E)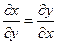 
;
$$$19 Жалпы интегралын табыңыз: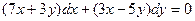 
.
A)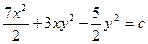 
;
B) 
;
C) 
;
D) 
;
E) 
;
$$$20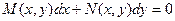 
теңдеуін 
функциясына көбейту арқылы толық дифференциалдыққа келтіруге болса, қалай аталады?
A) көбейткіш;
B) дифференциалдық көбейткіш;
C) интегралдаушы көбейткіш;
D) дифференциал;
E) туынды;
$$$21 Теңдеуді шешіңіз: 
.
A) 
;
B) 
;
C) 
;
D) 
;
E) 
;
$$$22 Лагранж теңдеуі?
A)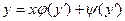 
;
B) 
;
C) 
;
D)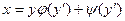 
;
E) 
;
$$$23 Теңдеуді шешіңіз: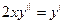 
A) 
;
B) 
;
C) 
;
D)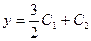 
;
E)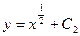 
;
$$$24 Клеро теңдеуі?
A)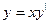 
;
B)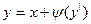 
;
C) 
;
D)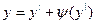 
;
E) 
;
$$$25 Клеро теңдеуінің шешімі?
A) 
;
B) 
;
C)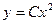 
;
D)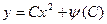 
E)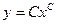 
;
$$$26Ретін төмендетуге болатын жоғарғы ретті диф.теңдеу?
A) 
;
B) 
;
C) 
;
D) ;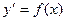
E) ;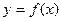
$$$27 Теңдеуді шешіңіз:
A) 
;
B)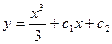 
;
C)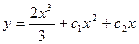 
;
D)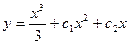 
;
E) ;
$$$28 Теңдеуді шешіңіз: 
A) 
;
B)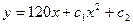 
;
C)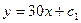 
;
D) 
;
E) 
;
$$$29 Жоғарғы ретті біртекті теңдеу?
A) 
;
B) 
;
C)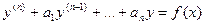 
;
D) 
;
E) 
;
$$$30 Жоғарғы ретті біртекті емес теңдеу?
A) ;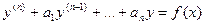
B) 
;
C)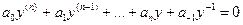 
;
D)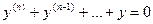 
;
E) 
;
$$$31 Вронский анықтауышы?
A) 
;
B) 
;
C) 
;
D)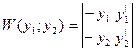 
;
E) 
;
$$$32Екінші ретті тұрақты коэффициентті біртекті диф.теңдеу?
A) 
;
B)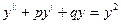 
;
C)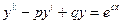 
;
D)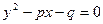 
;
E) 
;
$$$33 
. Жалпы шешімі?
A)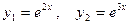 
;
B) 
;
C) 
;
D)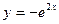 
;
E)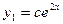 
;
$$$34 L(y)=f(x) теңдеуінің сәйкес L(y)=0 біртекті теңдеуінің жалпы шешімі белгілі болса, онда тәуелсіз тұрақтыларды С1(х),....,Сn(x)-функцилар деп берілген теңдеуді қанағаттандыратындай етіп таңдап алу әдісі.
A) у2=у1z-алмастыруы арқылы іздейді;
B) у=с1у1+с2у2;
C) тәуелсіз тұрақтыларды вариациялау деп аталады;
D) фундаментальдық шешімдер жүйесі болады;
E) вронскиан- W(x)≠0;
$$$35 
. Жалпы шешімі?
A)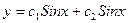 
;
B) 
;
C)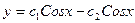 
;
D)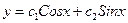 
;
E)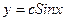 
;
$$$36 Теңдеуді шешіңіз: 
A)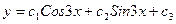 
;
B) 
;
C) 
;
D)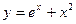 
;
E) 
;
$$$37 Теңдеуді шешіңіз: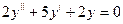 
A)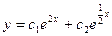 
;
B)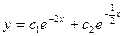 
;
C)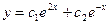 
;
D)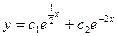 
;
E)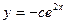 
;
$$$38 Екінші ретті тұрақты коэффициетті біртекті емес диф.теңдеу?
A) 
;
B) 
;
C) ;
D) 
;
E)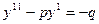 
;
$$$39 Теңдеуді шешіңіз: 
A)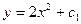 
;
B) 
;
C)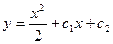 
;
D)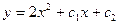 
;
E) 
;
$$$40 Теңдеуді шешіңіз: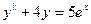 
A) 
;
B)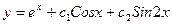 
;
C)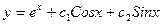 
;
D) 
;
E) 
;
$$$41Екінші ретті диф.теңдеуді шешудің Лагранж әдісі-?
A) тәуелсіз тұрақты шаманы варияциалау;
B) алмастыру:у!=р;
C) интегралдаушы көбейткішті қолдану;
D) 
;
E)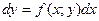 
;
$$$42Нормальдық диф.теңдеулер жүйесі:
A) 
;
B) 
;
C)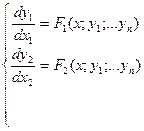 
;
D) ;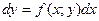
E)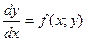 
;
$$$43 Нормальдық тұрақты коэффициентті диф.теңдеулер жүйесі?
A)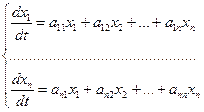 
;
B) 
;
C) 
;
D) 
;
E) 
;
$$$44 y″-3y′+2y=x − дербес шешімі (k1=1; k2=2)?
A) yg=x/2+3/4;
B) yg=(-x/6-1/2)x2;
C) y=c1e-x+c2e-2x;
D) y=c1e-x+c2ex-1/2sinx;
E) yg=x/2+3/4;
$$$45 у(n)=f(x) шешімін табу сатылары?
A) y(n-1)=∫f(x)dx+c1 ж.с.с. n-рет интегралдау;
B) y(k)=z, у(к+1)=z',….,осылайша ретін төмендету арқылы;
C) у'=dy/dx=p, у"=dp/dy.dy/dx=p'·p,… реті төмендетіледі;
D) μ(х,у)-интегралдаушы көбейткіш δ(μМ)/δу=δ(μN)/δx қанағаттандыруы керек;
E)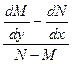 
- өрнегі (x+y)-тің функциясы болуы керек;
$$$46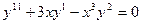 
теңдеуінің реті?
A) 3-ші ретті;
B) 2-ші ретті;
C) 1-ші ретті;
D) 4-ші ретті;
E) 5-ші ретті;
$$$47 Теңдеуді шешіңіз: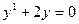 
.
A) 
;
B)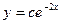 
;
C)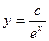 
;
D) 
E) ;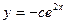
$$$48 y1-ysinx=ctgx теңдеудің типін анықтаныз?
A) Лагранж теңдеуі;
B) Клеро теңдеуі;
C) сызықтық тендеу;
D) біртекті теңдеу;
E) біртекті емес теңдеу;
$$$49 y′″-y=0 − шешімі?
A) y=c1ex+c2e2x;
B) y=c1e2x+c2xe2x;
C) y=c1ex+c2e-x/2cos√3/2x+c3e-x/2sin√3/2x;
D) y=c1cosx+c2xcosx+c3sinx+c4xsinx;
E) y= 1/(1-x);
$$$50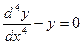 
. Мінездеме теңдеуі?
A)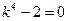 
;
B) 
;
C) 
;
D)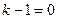 
;
E) 
;
$$$51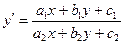 
теңдеуі ушін 
болса, теңдеуді біртектіге келтіретін алмастыру?
A) біртекті;
B) иә;
C) y/x=t(x);
D) х=u+x0; у=v+y0;
E) а1х+в1у=t(х) немесе а2х+в2у=t(x);
$$$52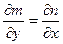 
шарты орындалса, m(x;y)dx+n(x;y)dy=0 қандай теңдеу?
A) Лагранж теңдеуі;
B) Клеро теңдеуі;
C) толық дифференциалдық тендеу;
D) біртекті теңдеу;
E) біртекті емес теңдеу;
$$$53 Теңдеуді шешіңіз y1 =3x:
A)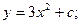 
B) 
C) 
D)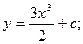 
E)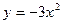 
;
$$$54 уу11-(у1)2=у3 теңдеуінің реті?
A) 3-ші ретті;
B) 2-ші ретті;
C) 1-ші ретті;
D) 4-ші ретті;
E) 5-ші ретті;
$$$55 
. Дербес шешімдері?
A)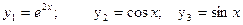 
;
B) 
;
C) 
;
D)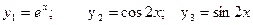 
;
E)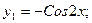 
;
$$$56 y11+y=0. Жалпы шешімі?
A) 
B) 
C) 
D) 
E)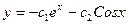 
;
$$$57Бірінші ретті диф.теңдеу?
A) 
;
B)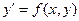 
;
C)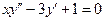 
;
D) 
;
E) 
;
$$$58 Теңдеуді шешіңіз: 
A)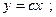 
B)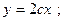 
C) 
D)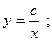 
E) 
;
$$$59 
теңдеуінің типі?
A) белгісіздері айырылған теңдеуі;
B) Клеро теңдеуі;
C) толық дифференциалдық тендеу;
D) біртекті теңдеу;
E) біртекті емес теңдеу;
$$$60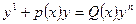 
теңдеуінің типі?
A) Лагранж теңдеуі;
B) Клеро теңдеуі;
C) сызықтық тендеу;
D) біртекті теңдеу;
E) біртекті емес теңдеу;
$$$61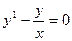 
. Жалпы шешімі?
A)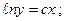 
B)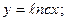 
C)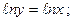 
D) 
E)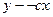 
;
$$$62 Теңдеуді шешіңіз: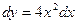 
?
A)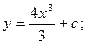 
B)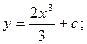 
C) 
D)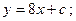 
E)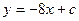 
;
$$$63 
. Жалпы шешімі?
A) 
B) 
C)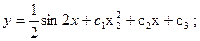 
D)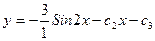 
;
E) 
;
$$$64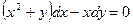 
. Интегралдаушы көбейткіші?
A)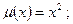 
B)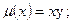 
C)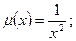 
D) 
E)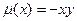 
;
$$$65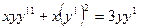 
. Қандай алмастыру керек?
A)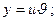 
B) 
C)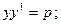 
D) 
E) 
;
$$$66Р Теңдеуді шешіңіз: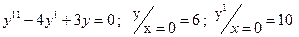 
?
A) 
B) 
C)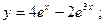 
D)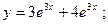 
E)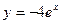 
;
$$$67 
алғашқы шарттары болса, қандай есептің шарттары?
A) Эйлера есебі;
B) Коши есебі;
C) Лагранж есебі;
D) Бернулли есебі;
E) Даламбер есебі;
$$$68 Тәуелсіз айнымалыны, белгісіз функцияны және......... байланыстыратын теңдеу диф.теңдеу деп аталады.
A) интегралды;
B) функцияның туындысын;
C) тұрақты шаманы;
D)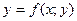 
;
E)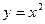 
;
$$$69 Теңдеуді шешіңіз: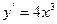 
A) 
B)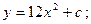 
C)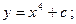 
D) 
E)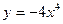 
;
$$$70 y″-4y′+4y=0 − шешімі?
A) y=c1ex+c2e2x;
B) y=c1e2x+c2xe2x;
C) y=c1ex+c2ex/2cos√3/2x+c3ex/2sin√3/2x;
D) y=c1cosx+c2xcosx+c3sinx+c4xsinx;
E) y= 1/(1-x);
$$$71 
, 
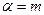мінездеме теңдеудің m еселі түбірі болса, дербес шешімін қай түрде іздеу керек?
A)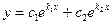 
;
B)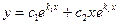 
;
C) 
;
D) 
;
E)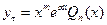 
, 
- копмүшелік;
$$$72 Теңдеуді шешіңіз: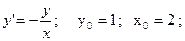 
A) 
B)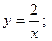 
C) 
D) 
E)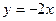 
;
$$$73 
теңдеуі қалай аталады?
A) интегралдық теңдеу;
B) 2-ші ретті диф.теңдеу;
C) 1-ші ретті диф.теңдеу;
D) квадраттық теңдеу;
E) интеграл;
$$$74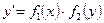 
. Жалпы шешімі?
A)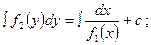 
B)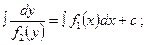 
C)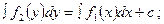 
D)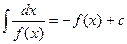 
;
E) 
;
$$$75 Теңдеуді шешіңіз: 
A)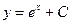 
;
B) 
;
C)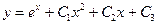 
;
D) 
;
E) 
;
$$$76 Қайсысы біртекті диф.теңдеу?
A) 
;
B)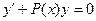 
;
C)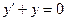 
;
D)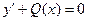 
;
E) 
;
$$$77 Теңдеуді шешіңіз: y 
A) y=y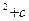 
;
B) y=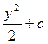 
;
C) y= xy;
D) y= ce 
;
E)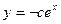 
$$$78 P(x)dx+Q(y)dy=0 теңдеуінің типі?
A) белгісіздері айырылған теңдеуі;
B) Клеро теңдеуі;
C) толық дифференциалдық тендеу;
D) біртекті теңдеу;
E) біртекті емес теңдеу;
$$$79 Теңдеуді шешіңіз: y 
A) y= 2x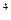 
+c;
B) y= 
;
C) y= 6x 
;
D) y= 
;
E) 
;
$$$80 Теңдеуді шешіңіз: y 
A) y=2cx;
B) y= ce ;
C) y= ce 
;
D) y= 2ce ;
E) 
;
$$$81 Қайсысы біртекті диф.теңдеу?
A) y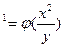 
;
B) y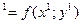 
;
C) y 
;
D) 
;
E) ;
$$$82 Қайсысы белгісіздерін айыруға болатын теңдеу?
A) 
;
B)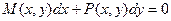 
;
C)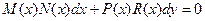 
;
D) ;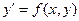
E) 
;
$$$83 Теңдеуді шешіңіз 
A) y= -Cosx;
B) y= -tgx;
C) 
;
D)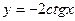 
;
E) 
;
$$$84 
-де 
m-рет қайталанатын мінездеме теңдеудің түбірі болса, онда дербес шешімін...
A)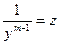 
;
B) 
, мұндағы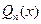 
коэфф. табу керек;
C) 
түрінде іздейді;
D) 
-түрінде іздейді;
E)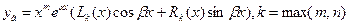 
түрінде іздейді;
$$$85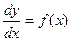 
. Жалпы шешімі?
A) 
;
B) 
;
C) 
;
D)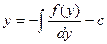 
;
E)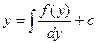 
;
$$$86 Теңдеуді шешіңіз: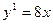 
A) 
;
B)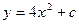 
;
C) 
;
D) ;
E) ;
$$$87 L(y)=eαx Pn(x)-теңдеуіндегі α-m рет қайталанатын мінездеме теңдеудің түбірі болса,дербес шешімін...
A) ;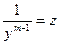
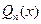B) , мұндағы коэфф. табу керек;
C) түрінде іздейді;
D) -түрінде іздейді;
E) 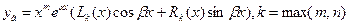түрінде іздейді;
$$$88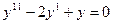 
теңдеуінің типін анықтаңыз.
A) белгісіздері айырылған теңдеуі;
B) 2-ші ретті тұрақты коэффициетті сызықтық диф.теңдеу;
C) толық дифференциалдық тендеу;
D) біртекті теңдеу;
E) біртекті емес теңдеу;
$$$89Қайсысы толық дифференциалдық теңдеу?
A) 
;
B) 
;
C)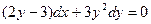 
;
D) 
;
E) 
;
$$$90Қайсысы Бернулли теңдеуі?
A)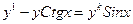 
;
B) 
;
C) 
;
D)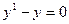 
;
E)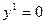 
;
$$$91 Теңдеуді шешіңіз: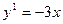 
A)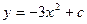 
;
B) 
;
C) 
;
D)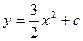 
;
E) ;
$$$92 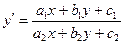теңдеуіндегі 
-
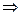
шешімі болса, теңдеуді біртектіге келтіру үшін қолданылатын алмастыру?
A) біртекті;
B) иә;
C) y/x=t(x);
D) х=u+x0; у=v+y0;
E) а1х+в1у=t(х) немесе а2х+в2у=t(x);
