Жоғарғы ретті тұрақты коэффициентті біртекті емес сызықтық теңдеулер

түріндегі теңдеу n-ретті біртекті емес сызықтық дифференциалдық теңдеу деп аталады.

Теорема. -сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімі оған сәйкес біртекті теңдеудің жалпы шешімі мен біртекті емес теңдеудің дербес шешімдерінің қосындысынан тұрады.

y = + y *,

мұндағы y - сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімі, - біртекті теңдеудің жалпы шешімі (оны табуды алдыңғы тақырыпта қарастырғанбыз), y * - сызықтық біртекті емес дифференциалдық теңдеудің дара шешімі, оны біртекті емес теңдеудің оң жағы f (x) функциясына ұқсас анықтаймыз. Ол қалай болатындығы төмендегі кестеде көрсетілген:

 

f (x)	Сипаттамалық теңдеудің түбірлері	Дара шешімнің түрі
1) eax Pn (x), мұндағы Pn (x) – n-дəрежелі берілген көпмүшелік	a саны – сипаттама теңдеудіңтүбірі емес a саны – сипаттама теңдеудіңr-еселі түбірі	y* = eax P*n (x) y ∗ = xr eaxP*n (x)
2) eax [ Pn(x) cos bx + + Qm (x) sin bx ]	a ± bi сандар жұбы – сипаттама теңдеудіңтүбірі емес a ± bi сандар жұбы – сипаттама теңдеудің r-еселі түбірі	y* = eax [ P*k(x) cos bx + Q*k (x) sin bx ], мұндағы k =max(m,n)     y* =xr eax [ P*k(x) cos bx + Q*k (x) sin bx ] мұндағы k =max(m,n)

 

 

Мысал 1: y ^{I V} + 8 y ''+16 y = cos x теңдеуінің жалпы шешімін тап.

Шешуі: y = + y *

1) =?

2) y *=?

f (x) = cosx Þ a ± bi = 0±1 i = i ≠ k₁, k₂,,k₃,k₄

y *=Acosx+Bsinx Þ (y *)^¢= -Asinx+Bcosx Þ

(y *)¢¢= -Acosx-Bsinx Þ (y *)¢²= Asinx-Bcosx Þ (y *)^iv= Acosx+Bsinx

Осы табылған туындыларды бастапқы берілген теңдікке қоямыз:

Acos x +Bsin x +8(-Acos x -Bsin x)+16(Acos x +Bsin x)=cos x

A мен B мəндерін y *-ны анықтау өрнегіне қоямыз:

y *= cos x

Демек, y = + y *= (C₁+xC₃)cos2x+ (C₂+xC₄)sin2x + cos x

Мысал 2: теңдеуінің жалпы шешімін тап.

Шешуі: f₁(x) + f₂(x) = x + (- sin x).

1)

2) 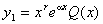түрінде іздейміз, мұндағы:

Þ

Сонымен,

3) f₂ (x) функциясын келесі түрде ізделік: .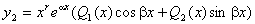

Þ

Сонымен,

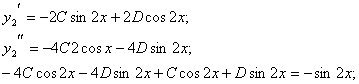
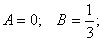болғандықтан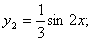

Ізделінді дара шешім: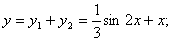

Ал біртекті емес дифференциалдық теңдеудің жалпы шешімі:

Аудиториялық жұмыстар

Берілген теңдеулердің жалпы шешімін тап:

1) 2 y ′′ + y ′ − y = 2 e^x Жауабы: y = С₁ e ^{− x} + С₂ e^{x/ 2} + e^x

2) y ′′ + a ² y = e^x Жауабы: y = С₁ cosax + С₂ sinax +

3) y ′′ − 7 y ′ + 6 y = sin x Жауабы: y = С₁ e ^{6 x} + С₂

4) y ′′ − 6 y ′ + 9 y = 2 x ² − x + 3 Жауабы:

5) y ′′ − 2 y ′ + 2 y = 2 x Жауабы: y = e^{x (( c} ₁ ^{cos x + c} ₂ ^{sin x )+ x )−1}

6) y ′′ + 4 y ′ − 5 y = 1 Жауабы: y = С₁ e^x + С₂ e ^-5x - 0,2

7) у" -2у ' +у= 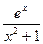Жауабы:у=е ^х (С₁+C₂x-ln +x arctgx)

Й жұмыстары

Берілген теңдеулердің жалпы шешімін анықта.

8) y "−3 y ′ + 2 y = f (x), мұнда f (x) келесі функциялар түрінде берілген:

 

а) 10 e ^{− x}

ə) 3 e ^{2 x}

б) 2sin x

в) 2 x ³ − 30

г)2 e^x cos

д) x − e ^{−2 x} +1

е) e^x (3 − 4 x)

ж) 3 x + 5sin 2 x

з) 2 e^x − e ^{−2 x}

и) sin x sin2 x

к) shx

Жауаптары: y = C₁ e^x + C₂ e ^{2 x} + y *, мұнда y * тең:

а) 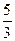e ^{− x}

ə) 3 xe ^{2 x}

б)

в)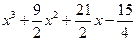

г) -8/5 +e^x(cosx/2 +2sinx/2)

д)

 

е) e^x (2 x ² + x)

ж) (9+3cos2x- sin2x)

з) -2 xe^x- e^{- 2 x}

и)

к) - e^-x- xe^x

9) 2 y "+5 y ′ = f (x), егер f (x) тең:

а) 5 x ² − 2 x −1

ə) e^x

б) 29cos x

в) cos² x

г) 0,1 e ^{−2,5 x} − 25sin 2,5 x

д) 29 x sin x

е) 100 x ⋅ e ^{− x} ⋅ cos x

ж) 3 сh x

Жауабы: y = C₁ + C₂ e^{- 5/2 x} + y *, мұнда y * тең:

 

а)

ə) 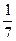e^x

б)5sin x − 2cos x

в)

г)cos2,5 x +sin2,5 x −0,02 xe ^{−2,5 x}

д)

е) e ^{− x} [(10 x +18)sin x − (20 x +1)cos x ]

ж)

 

Жоғарғы ретті тұрақты коэффициентті біртекті емес