Криволінійні інтеграли.
Криволінійні інтеграли І роду
Криволінійні інтеграли І роду,
їх властивості та методи обчислення.
Задача, що приводить до поняття криволінійного інтеграла І роду – задача про масу дуги кривої неоднорідної щільності.

| Нехай на площині хОу задана кусково гладка крива АВ. У кожній її точці визначена та неперервна функція  . Якщо висунути вимогу, що функція . Якщо висунути вимогу, що функція  набуває тільки невід’ємних значень, тоді її можна інтерпретувати як набуває тільки невід’ємних значень, тоді її можна інтерпретувати як
|
| Рис. 1 |
функцію щільності (густини) кривої.
Поставимо задачу обчислення маси дуги кривої АВ.
Розіб’ємо дугу АВ на n частин точками:
 .
.
Довжину кожної ділянки розбиття позначимо  .
.
Тепер на кожній ділянці розбиття випадковим чином оберемо точки  . Щільність кожної ділянки розбиття будемо вважати сталою величиною і рівною щільності у точці
. Щільність кожної ділянки розбиття будемо вважати сталою величиною і рівною щільності у точці  :
:  . Тоді маса кожної ділянки розбиття наближено буде дорівнювати:
. Тоді маса кожної ділянки розбиття наближено буде дорівнювати:
 ,
,
а маса всієї кривої буде дорівнювати:
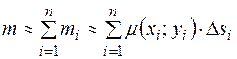 . .
| (1) |
Сума (1) є інтегральною для функції  . Якщо кількість точок розбиття прямує до нескінченності:
. Якщо кількість точок розбиття прямує до нескінченності:  , а максимальна довжина ділянки розбиття
, а максимальна довжина ділянки розбиття  , тоді інтегральна сума (1) має скінченну границю, яку називають криволінійним інтегралом першого роду і позначають так:
, тоді інтегральна сума (1) має скінченну границю, яку називають криволінійним інтегралом першого роду і позначають так:

 . .
| (2) |
Можливі позначення криволінійного інтегралу І роду: 

 та інші.
та інші.
Зауваження. Якщо інтегрування відбувається по замкненому контуру, тоді криволінійного інтегралу І роду позначають  .
.
Теорема про існування криволінійного інтегралу І роду. Якщо функція  неперервна у кожній точці кусково гладкої кривої АВ, тоді криволінійний інтеграл І роду від функції
неперервна у кожній точці кусково гладкої кривої АВ, тоді криволінійний інтеграл І роду від функції  по кривій АВ існує. Його значення (тобто значення границі (2)) не залежить ні від способу розбиття кривої АВ на ділянки, ні від способу вибору на них точок
по кривій АВ існує. Його значення (тобто значення границі (2)) не залежить ні від способу розбиття кривої АВ на ділянки, ні від способу вибору на них точок  .
.
Зауваження. Фізичний зміст криволінійного інтеграла І роду полягає у тому, що його значення відповідає масі дуги кривої, по якій відбувається інтегрування, якщо під інтегральну функцію розглядати як щільність (густину) кривої.

| Геометричний зміст криволінійного інтеграла І роду полягає у тому, що його значення відповідає площі циліндричної поверхні, напрямна якої збігається з кривою АВ, а твірні паралельні Оz і мають довжину  . .
|
| Рис. 2 |
Властивості криволінійного інтеграла І роду
1. Значення криволінійного інтегралу не залежить від напрямку обходу кривої, по якій виконується інтегрування:
 . .
|
Зауваження. Це єдина властивість криволінійного інтеграла І роду, яка відрізняється властивостей визначеного інтеграла. Вона пояснюється тим, що множник  у формулі інтегральної суми (2) визначає довжину ділянки розбиття дуги, тобто завжди є додатним.
у формулі інтегральної суми (2) визначає довжину ділянки розбиття дуги, тобто завжди є додатним.
2. Постійний множник можна виносити за знак криволінійного інтеграла:
 , де , де  . .
|
3. Криволінійний інтеграл від суми (різниці) функцій дорівнює сумі(різниці) інтегралів від кожної функції окремо:
 . .
|
4. Якщо криву АВ розбито точкою С на дві дуги, тоді
 . .
|
5. Якщо в усіх точках кривої АВ виконується нерівність
 , тоді
, тоді
 . .
|
6. Криволінійний інтеграл І роду від одиниці дорівнює довжині дуги, по якій відбувається інтегрування:
 . .
|
7. Теорема про середнє значення функції на дузі АВ. Якщо функція  неперервна на дузі кривої АВ, то на цій дузі знайдеться така точка
неперервна на дузі кривої АВ, то на цій дузі знайдеться така точка  , що виконується рівність:
, що виконується рівність:
 . .
|






