За умов нечіткого (з точки зору математики) опису характеристик системи їх зручно представити у вигляді лінгвістичних змінних, значенням яких є поняття чи речення вербального опису. Наприклад, лінгвістична змінна складність має значення: низька, висока, не дуже висока.
Найчастіше структуру лінгвістичної змінної для задач прийняття рішень розглядають у такому вигляді: <Z, T, А >, де Z – ім’я лінгвістичної змінної, яка є агрегованою характеристикою системи; Т – множина лінгвістичних значень; A = 
– множина базових змінних. Кожен елемент множини A задає сукупність певних властивостей системи. Оскільки ці властивості формуються внаслідок реалізації певної альтернативи, то в задачі прийняття рішень під множиною базових змінних A = будемо розуміти множину альтернатив, що забезпечує певні властивості системи. Декомпозиція агрегованої характеристики зі значенням із множини Т лінгвістичних значень дозволяє отримати множину нечітких змінних { 
,…, 
} – нечітких характеристик властивостей системи, на основі яких можна побудувати критерії зважування альтернатив. З цією метою для кожної нечіткої характеристики властивостей системи вводять функції відповідності 
властивостям, які забезпечуватимуть альтернатив:
.
Критерій-агрегат за даних умов формулюється так: “Найкращою є та альтернатива, яка в найбільшій мірі забезпечує усі потрібні властивості системи, тобто властивості, що описуються нечіткою множиною і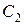 
і,..., і ”. Тоді нечітка множина агрегованої характеристики властивостей формується так:
E = 
…
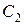
Функція відповідності властивостей, які забезпечує 
альтернатива властивостям відображеним в агрегованій характеристиці, матиме вигляд
= 
.
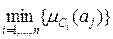Згідно обраного критерію, найкращою буде та альтернатива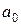 
, яка забезпечує = 
.
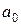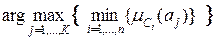Розглянутий підхід до побудови агрегованого критерію прийняття рішень за умов нечітко заданих критеріїв не враховує різної важливості характеристик системи. У випадку різної важливості характеристик, нечітка множина агрегованої характеристики властивостей має такий вигляд
E =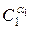 
… 
,
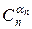де 
, 
,..., 
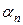- коефіцієнти важливості характеристик.
Функція відповідності властивостей в цьому випадку знаходиться так:
= 
.
Для визначення коефіцієнтів , ,..., 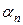можна використати процедуру по-парного порівняння критеріїв на основі даних такої таблиці.
Відносна важливість критеріїв
| Значення елементів
|
| Рівноважливість критеріїв | |
| Трохи важливий | |
| Відчутно важливий | |
| Набагато важливіший | |
| Важливіший | |
| Інші випадки | 2, 4, 6, 8 |
В таблиці: 
, 
Процедура знаходження коефіцієнтів важливості наступна:
1. Знаходження власних чисел матриці парних порівнянь В, складеної із елементів із розв’язку такого рівняння:
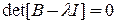
Розв’язком рівняння будуть власні числа:
2. Знаходження серед власних чисел максимального:
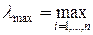
3. Знаходження власного вектора для максимального власного числа із системи рівнянь:
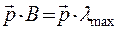
4. Розрахунок , ,...,
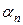
де 
i -та компонента власного вектора
