Министерство образования и науки Российской федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ростовский государственный строительный университет»
Утверждено
на заседании кафедры физики
08 февраля 2012 г.
Зав. кафедрой физики
__________________/Н.Н. Харабаев/
Учебно-методическое пособие
КОНСПЕКТ ЛЕКЦИЙ по физике
(для бакалавриата всех профилей)
Ростов-на-Дону
Учебно-методическое пособие. Конспект лекций по физике (для бакалавриата всех профилей). – Ростов н/Д: Рост. гос. строит. ун-т, 2012. – 103 с.
Содержится конспект лекций по физике, основанный на учебном пособии Т.И. Трофимовой «Курс физики» (изд-во Высшая школа).
Состоит из четырех частей:
I. Механика.
II. Молекулярная физика и термодинамика.
III. Электричество и магнетизм.
IV. Волновая и квантовая оптика.
Предназначено для преподавателей и студентов в качестве теоретического сопровождения лекций, практических и лабораторных занятий с целью достижения более глубокого усвоения основных понятий и законов физики.
Рекомендуется для самостоятельной работы студентов бакалавриата очной и заочной форм обучения всех профилей по направлениям:
270800 «Строительство»
270200 «Реконструкция и реставрация архитектурного наследия»
280700 «Техносферная безопасность»
190700 «Технология транспортных процессов»
190600 «Эксплуатация транспортно-технологических машин и комплексов»
230400 «Информационные системы и технологии»
230700 «Прикладная информатика»
120700 «Землеустройство и кадастр»
261400 «Технология художественной обработки материалов»
221700 «Стандартизация и метрология»
100800 «Товароведение»
УДК 531.383
Составители: проф. Н.Н.Харабаев
доц. Е.В.Чебанова
проф. А.Н. Павлов
Редактор Н.Е.Гладких
Темплан 2012 г., поз.
Подписано в печать
Формат 60х84 1/16. Бумага писчая. Ризограф. Уч.-изд.л. 4,0.
Тираж 100 экз. Заказ
_________________________________________________________
Редакционно-издательский центр
Ростовского государственного строительного университета
334022, Ростов-на-Дону, ул. Социалистическая, 162
© Ростовский государственный
строительный университет, 2012
ЧАСТЬ I. Механика
Тема 1. Кинематика поступательного и вращательного движения.
Кинематика поступательного движения
Положение материальной точки А в декартовой системе координат в данный момент времени определяется тремя координатами x, y и z или радиусом-вектором 
– вектором, проведенным из начала системы координат в данную точку (рис. 1).
Движение материальной точки определяется в скалярном виде кинематическими уравнениями: x = x(t), у = y(t), z = z(t),
или в векторном виде уравнением: 
.
Траектория движения материальной точки – линия, описываемая этой точкой при её движении в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.
Материальная точка, двигаясь по произвольной траектории, за малый промежуток времени D t переместиться из положения А в положение В, пройдя при этом путь D s, равный длине участка траектории АВ (рис. 2).
Рис. 1 Рис. 2
Вектор 
, проведенный из начального положения движущейся точки в момент времени t в конечное положение точки в момент времени(t+ D t), называется перемещением, то есть 
.
Вектором средней скорости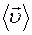 
называется отношение перемещения к промежутку времени D t, за который это перемещение произошло:
.
Направление вектора средней скорости 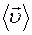совпадает с направлением вектора перемещения .
Мгновенной скоростью 
(скоростью движения в момент времени t) называется предел отношения перемещения к промежутку времени D t, за который это перемещение произошло, при стремлении D t к нулю:
,
где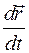 
– первая производная от функции 
по времени t, которую принято обозначать также в виде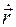 
.
Вектор мгновенной скорости направлен по касательной, проведенной в данной точке к траектории в сторону движения. При стремлении промежутка времени D t к нулю модуль вектора перемещения 
стремится к величине пути D s, поэтому модуль вектора может быть определен через путь D s:
.
Если скорость движения точки со временем изменяется, то быстрота изменения скорости движения точки характеризуется ускорением.
Средним ускорением 
в интервале времени от t до (t + D t) называется векторная величина, равная отношению изменения скорости 
(
) к промежутку времени D t, за который это изменение произошло: 
.
Мгновенным ускорением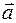 
или ускорением движения точки в момент времени t называется предел отношения изменения скорости к промежутку времени D t, за который это изменение произошло, при стремлении D t к нулю:
,
где 
– первая производная от функции 
по времени t,
– вторая производная от функции по времени t.
Эти производные принято обозначать соответственно в виде: 
и 
.
Вектор ускорения 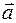может быть разложен на две составляющие:тангенциальную 
и нормальную 
, то есть:
.
Тангенциальная составляющая определяет быстроту изменения модуля скорости : 
.
Вектор направлен по касательной к траектории движения и для ускоренного движения совпадает с направлением вектора скорости , а для замедленного движения – противоположен вектору скорости .
Нормальная составляющая определяет быстроту изменения направления скорости : 
,
где r – радиус кривизны траектории движения.
Вектор направлен по нормали к траектории движения к центру ее кривизны (поэтому нормальную составляющую ускорения называют также центростремительным ускорением).
