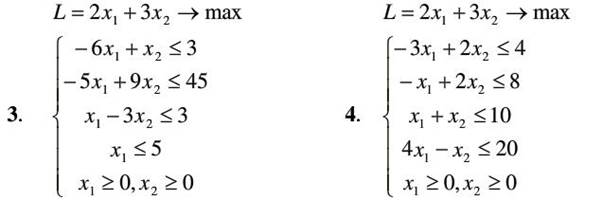
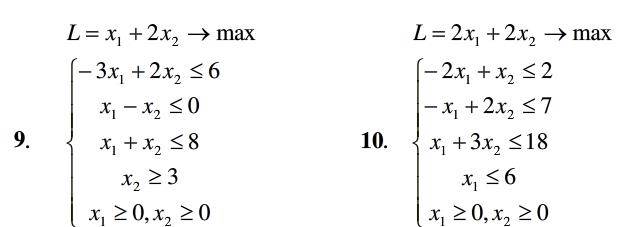
Задание 4
Решить задачу линейного программирования симплексным методом.
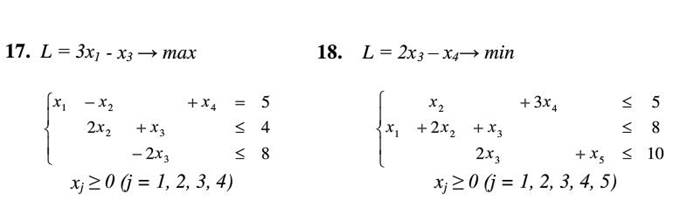
Задание 5
На три базы А1,А2,А3 поступил однородный груз в количестве а1 тонн на базу А1; а2 тонн на базу А2; а3 тонн на базу А3. Полученный груз требуется привезти в пять пунктов: b1 тонн в пункт В1; b2 тонн в пункт В2; b3 тонн в пункт В3; b4 тонн в пункт В4; b5 тонн в пункт В5.
Расстояние между пунктами отправления (базами) и пунктами назначения (потребителями) указаны в таблице (матрица расстояний D).
Стоимость перевоза пропорциональна количеству груза и расстоянию, на которое этот груз перевозится. Спланировать перевозки так, чтобы их общая стоимость была наименьшей.
Указание.
Ввиду пропорциональности затрат количеству груза и расстоянию для решения задачи достаточно минимизировать общий объем плана, выраженный в тонно-километрах.
1.
2.
3.
4.
5.
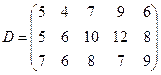
6.
7.
8.
9.
10.
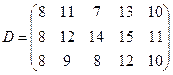
Задание 6
Для приготовления различных изделий А и В используется три виды сырья. На производства единицы изделия А требуется затратить сырья первого вида а1 кг, сырья второго вида а2 кг, сырья третьего вида а3 кг. На производство единицы изделия В требуется затратить сырья первого вида b1 кг, сырья второго вида b2 кг, сырья третьего вида b3 кг.
Производство обеспечено сырьем первого вида в количестве p1 кг, сырьем второго вида в количестве р2 кг, сырьем третьего вида в количестве р3 кг.
Прибыль от реализации единицы готового изделия А составляет а руб., а изделия В- 
руб.
Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации. Решить задачу симплексным методом путем преобразования симплекс-таблиц.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
Задание 7.
В пунктах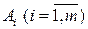 
находится некоторый продукт в объемах 
единиц. Спрос на этот продукт в пунктах потребления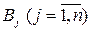 
, составляет соответственно 
единиц. Известна стоимость 
перевозок единицы груза из пункта 
в пункт 
. Требуется найти план перевозок продукции из пунктов производства в пункты назначения, минимизирующий суммарные затраты по доставке продукции. Требуется: а) составить математическую модель задачи; б) найти оптимальный план перевозок продукции методом потенциалов при условии, что продукция из указанного пункта 
вывозится полностью; в) дать анализ решения. Числовые данные , , 
даны в табл. 1.
Таблица 1
| № варианта | Числовые данные , , .
|
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
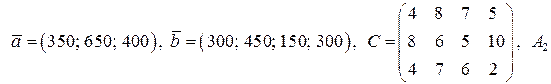
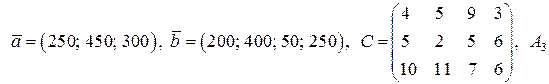
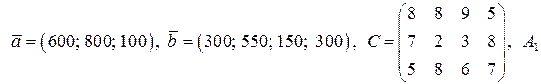
Задание 8.
Пусть предприятие выпускает n видов продукции 
. Для их изготовления требуется затратить m видов ресурсов 
. Известны следующие величины: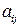 
–- количество единиц ресурса вида 
необходимого на изготовление единицы продукции 
; 
–-количество ресурса вида , которым располагает предприятие; 
–- стоимость единицы продукции 
. Требуется найти план предприятия, обеспечивающий ему максимальную прибыль, при этом: а) составить математическую модель задачи; б) найти план выпуска продукции симплекс-методом, привести экономический смысл переменных, участвующих в решении задачи; в) построить математическую модель двойственной задачи; г) из решения исходной задачи, используя соответствие между переменными пары взаимодвойственных задач, найти решение двойственной задачи; д) указать наиболее дефицитный и избыточный ресурс, если он есть.
Необходимые числовые данные приведены в табл. 2.
.
Таблица 2
| № варианта | Данные А, В, С. |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
