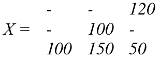Транспортная задача является специальной задачей линейного программирования.
Суть ее заключается в следующем. Есть m поставщиков грузов А1, А2, …, Аm и n потребителей B1, B2, …, Bn этих грузов. Известны запасы грузов у поставщиков а1, а2, …, аm и потребности в этих грузах b1, b2, …, bn соответственно, а также тарифы перевозок сij.
Требуется:
1. Все запасы изъять.
2. Все потребности удовлетворить.
3. Чтобы стоимость доставки грузов была минимальной.
Математическая модель задачи следующая:
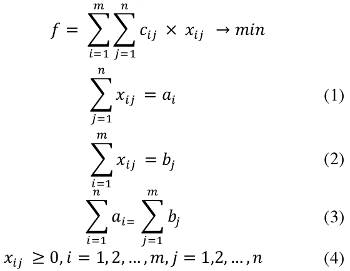
Как видим, математическая модель записана в каноническом виде, так как в ней присутствует условие равновесия (2), но это идеальный случай. Чаще всего можно столкнуться со следующим:
a. запасы превышают потребности и тогда приходится вводить фиктивного потребителя с нулевым тарифом;
b. потребности превышают запасы – вводят фиктивного поставщика с нулевым тарифом.
Почему тарифы равны нулю? Вывод очевиден – надо следовать критерию задачи.
Более подробную информацию по теории транспортной задачи можно посмотреть в учебниках по исследованию операций либо математическому программированию.
Любая задача ЛП, в том числе и транспортная задача, решается в два этапа.
Сначала находят опорный план, затем его подвергают анализу и в конечном итоге находят оптимальный план. Для транспортной задачи существуют и прямые методы – это распределительный метод, дельта-метод и метод дифференциальных рент. Но независимо от применяемого математического метода полученное решение проверяют на оптимальность с помощью метода потенциалов.
Рассмотрим задачу: имеются три поставщика грузов и три потребителя этих грузов. Запасы грузов составляют 150, 100 и 300 ед., потребности в них равны 100, 250 и 200 ед. соответственно. Тарифы перевозок также известны:
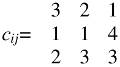
Найти оптимальный план доставки этих грузов.
Следует отметить, что для нахождения опорного плана разработано несколько методов, которые делятся на две группы: методы, которые учитывают тарифы перевозок и методы, не учитывающие их. Вполне понятно, что первая группа методов дает план, близкий к оптимальному, а вторая группа дает грубое приближение.
Вначале найдем опорный план с помощью диагонального способа без учета тарифов.
Для решения задачи составляется таблица перевозок:
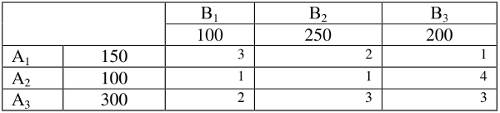
Правила заполнения таблицы несложные. Заполнение начинают с левой верхней клетки, в которую записывают грузопоставку исходя из наличия груза и потребности в нем. Наличие груза у поставщика А1 составляет 150 ед. а потребность потребителя В1 в грузе равна 100 ед. Запишем этот груз полностью, а остаток 50 ед. запишем следующему потребителю, третью ячейку вычеркнем, так как весь груз у первого поставщика изъят:
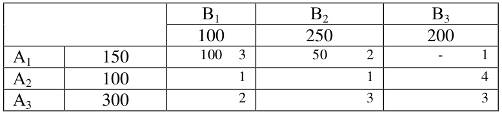
Подобные действия произведем со вторым и третьим поставщиком. Получим таблицу перевозок:
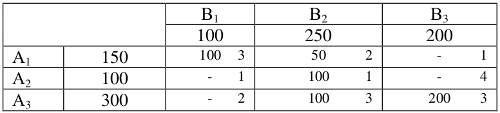
Как видим, при распределении грузов тарифы не учитывались. Расходы на доставку грузов составляют:
f = 3×100 + 2×50 + 1×100 + 3×100 + 3×200 = 1400 у.е. Найдем опорный план методом минимального элемента с учетом тарифов перевозок и сравним решения. Составим такую же таблицу перевозок, но вот порядок заполнения будет отличен от предыдущего случая:
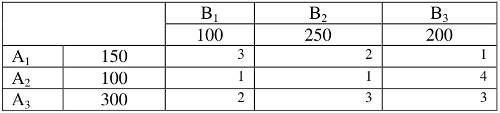
Грузопоставки начнем вписывать в клетку, которая имеет наименьший тариф. Если таких клеток несколько, то начинать записывать можно в любую из них. Минимальный тариф в таблице равен единице, а так как таких клеток три, то выберем первой например ячейку А1В3. Размер грузопоставки определяется исходя из наличия груза у поставщика и потребности потребителя. Наличие груза у первого поставщика равно 150 ед., потребность равна 200 ед. Мы забираем весь груз у А1 и записываем:
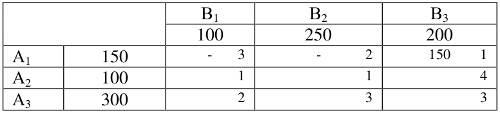
Заполняем следующую клетку с тарифом, равным единице:
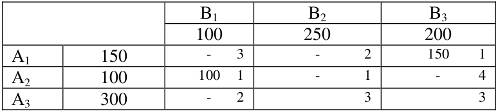
Оставшиеся клетки с одинаковым тарифом последовательно заполняем:

Вычислим транспортные расходы: f = 1×100 + 3×50 + 1×150 + 3×250 = 1150 у.е. Как видим, опорный план, полученный методом минимального элемента, дает лучший результат, чем диагональный способ. После того, как получено допустимое решение, его надо проверить на оптимальность с помощью метода потенциалов. Перед проверкой убеждаемся, что число заполненных клеток равно соотношению m+n-1. В нашей таблице их 3+3-1=5.
Признак оптимальности: решение оптимально, если во всех свободных клетках выполняется неравенство: αi + cij ≥ βj, где αi и βj – потенциалы, cij – тарифы перевозок. Вычислим αi и βj с помощью выше указанного неравенства:

Принято считать, что α1 всегда равно 0. Если не сделать это допущение, то задача не будет иметь решение. Вычисления остальных значений потенциалов производят по базовым (заполненным) клеткам:
α1 = 0
β1 = 3 + 0 = 3
β2 = 2 + 0 = 2
α2 = 2 — 1 = 1
α3 = 2 — 3 = -1
β3 = -1 + 3 = 2
Проверку на оптимальность делают по свободным клеткам с помощью этого же неравенства:
А1В3: 0 + 1 ≥ 2 – нет
А2В1: 1 + 1 ≥ 3 – нет
А2В3: 1 + 4 ≥ 2 – да
А3В1: -1 + 2 ≥ 3 – нет
В результате проверки мы выявили три недостаточные клетки. Находим цикл пересчета:
цикл пересчета – это ход ладьи по базовым клеткам с чередованием знаков «+» и «-», начиная с недостаточной клетки и замыкаясь в ней же.
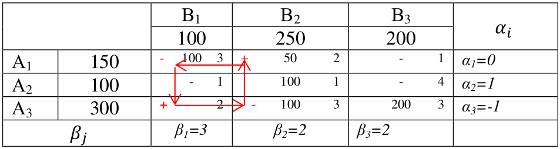
В клетках с минусовыми отметками выбирает минимальное число. В нашем случае это число равно 100. Пересчет делают следующим образом: где стоит знак «-» это число отнимают, а где «+» то прибавляют. Значения, не входящие в цикл пересчета переписывают без изменений. Получает таблицу, в которой соотношение m+n-1 не выполняется, и поэтому выбираем клетку с минимальным тарифом и, проставляя в ней ноль, считаем ее условно базовой:
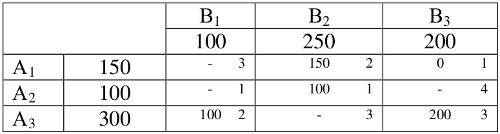
Вначале транспортные расходы составляли 1400 у.е. Считаем сейчас: f2 = 2×100 + 2×150 + 1×100 + 3×200 = 1200 у.е. Уменьшение этого показателя говорит о том, что мы на верном пути. Полученное решение снова проверяем на оптимальность:
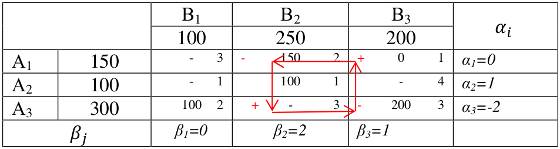
Проверка выявляет одну недостаточную клетку, для которой находим цикл пересчета:
А1В1: 0 + 3 ≥ 0 – да
А1В3: 1 + 0 ≥ 1 – да
А2В1: 1 + 1 ≥ 0 – да
А3В2: -2 + 3 ≥ 2 – нет
В отрицательных клетках из двух значений выбираем число 150, которое отнимаем, где знак «-» и прибавляем где знак «+»:

Транспортные расходы:f3 = 2×100 + 3×150 + 1×100 + 1×150 + 3×50 = 1050 у.е.
Проверяем снова на оптимальность и убеждаемся, что найден оптимальный план:
А1В1: 0 + 3 ≥ 0 – да
А1В2: 0 + 2 ≥ 1 – да
А2В1: 0 + 1 ≥ 0 – да
А2В3: 0 + 4 ≥ 1 – да
Ответ: f = 1050 у.е.