Пример решения задачи линейного программирования симплекс-методом

Пример. Найти максимум функции при ограничениях

Решение.

Шаг I. Вводим добавочные неотрицательные переменные и сводим данную систему неравенств к эквивалентной ей системе уравнений

Введённые добавочные переменные принимаем за основные, так как в этом случае базисное решение системы легко находится. Тогда и - неосновные переменные.

Выразив основные переменные через неосновные, получим

Следовательно, данному разбиению переменных на основные и неосновные соответствует базисное решение , которое является недопустимым (две переменные отрицательны), а поэтому оно не оптимальное. От этого базисного решения перейдём к улучшенному.

Чтобы решить, какую переменную следует перевести из неосновных в основные, рассмотрим любое из двух имеющихся уравнений последней системы с отрицательными свободными членами, например второе. Оно показывает, что в основные переменные можно перевести и , так как в этом уравнении они имеют положительные коэффициенты (следовательно, при их увеличении, а это произойдёт, если переведём любую из них в основные переменные, переменная увеличится).

Попробуем перевести в основные переменную . Чтобы установить, какую переменную следует перевести из основные в неосновные, найдём абсолютную величину наименьшего отношения свободных членов системы к коэффициентам при . Имеем 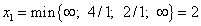. Оно получено из третьего уравнения, показывающего, что в неосновные нужно перевести переменную , которая в исходном базисном решении положительна. Следовательно, полученное базисное решение, как и исходное, содержит две отрицательные компоненты, т. е. при переходе к такому базисному решению улучшения не произойдёт.

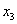Если же перевести в основные переменную , то наименьшее отношение свободных членов к коэффициентам при составит . Оно получено из первого уравнения, в котором свободный член отрицателен. Следовательно, переводя в основные, а в неосновные переменные, мы получим базисное решение, в котором число отрицательных компонент на единицу меньше, чем в исходном. 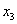Поэтому остановимся на этой возможности: переводим в основные, а в неосновные переменные. Поэтому в приведённой выше системе уравнений выделенным оказалось первое уравнение.

Шаг II.

Основные переменные , неосновные переменные .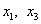

Выразим новые основные переменные через новые неосновные, начиная с выделенного на шаге I уравнения. В результате получим

Следовательно, имеем новое базисное решение , которое также является недопустимым, а поэтому не оптимальным. Но в нём, как мы и предвидели, только одна переменная отрицательна (а именно ).

От полученного базисного решения необходимо перейти к другому. Рассмотрим уравнение с отрицательным свободным членом, т. е. второе уравнение. Оно показывает, что в основные переменные можно перевести и 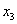. Переведём в основные переменные . Найдём наименьшее из абсолютных величин отношений свободных членов системы к коэффициентам при . Имеем . Значит, в неосновные переменные нужно перенести . Так как наименьшее отношение получено из второго уравнения, то его выделяем. В новом базисном решении уже не окажется отрицательных компонент, т. е. оно является допустимым.

В особых случаях решение завершается на II шаге: это, например, случаи, когда максимум целевой функции - бесконечность и когда система не имеет ни одного решения.

Шаг III.

Основные переменные: , неосновные переменные: . Выразив основные переменные через неосновные, получим

Новое базисное решение имеет вид 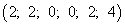. Является ли оно оптимальным, можно установить, если выразить линейную форму через неосновные переменные рассматриваемого базисного решения. Сделав это, получим . Так как мы ищем максимум линейной формы, а нашли лишь одно допустимое решение, то продолжим перебор.

Переводим в число основных переменную , имеющую больший положительный коэффициент. Находим . Это наименьшее отношение получено из третьего уравнения системы, поэтому его выделяем. Оно показывает, что при переменная 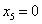и поэтому перейдёт в число неосновных.

В некотором особом случае решение завершается на III шаге: это случай, когда оптимальное решение - не единственное.

Шаг IV.

Основные переменные: , неосновные переменные: 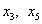. Выразив основные переменные через неосновные, получим

Линейная форма, выраженная через те же неосновные переменные, примет вид . Продолжим перебор для поиска максимума.

Увеличение линейной формы возможно при переходе к новому базисному решению, в котором переменная 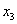является основной. Находим . Это наименьшее отношение получено из четвёртого уравнения системы и показывает, что при переменная и переходит в число неосновных.

Шаг V.

Основные переменные: 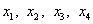, неосновные переменные: . Выразив основные переменные через неосновные, получим

Линейная форма, выраженная через неосновные переменные нового базисного решения, имеет вид . Критерий оптимальности для случая максимизации линейной формы выполнен. Следовательно, базисное решение 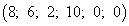является оптимальным, а максимум линейной формы

Пример решения

Решить задачу линейного программирования с помощью программы «Поиск решения» в MS Excel.

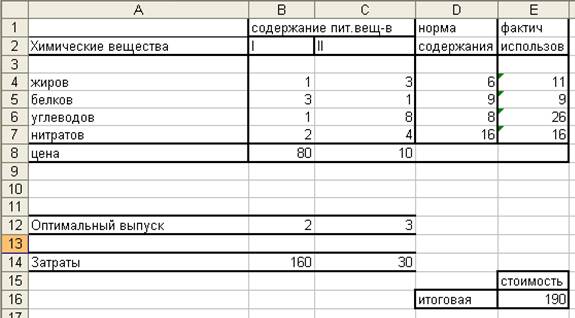
Формулировка задачи: Рацион для питания животных на ферме состоит из двух видов кормов I и II. Один кг корма I стоит 80 д.е. и содержит: 1 ед. жиров, 3 ед. белков, 1 ед. углеводов, 2 ед. нитратов. Один кг корма II стоит 10 д.е. и содержит: 3 ед. жиров, 1 ед. белков, 8 ед. углеводов, 4 ед. нитратов. Составить наиболее дешевый рацион питания, обеспечивающий жиров не менее 6 ед., белков не менее 9 ед., углеводов не менее 8 ед., нитратов не более 16 ед.

	содержание пит.веществ	норма содержания
Химические вещества	I	II

жиры
белки
углеводы
нитраты
Стоимость 1 кг

Экономико-математическая модель задачи:

Пусть Х₁– количество корма I, X₂– количество корма II, тогда суммарная стоимость будет равна:

Z=80X₁+10X₂ → min (1)

Составим систему ограничений:

(2)
X₁, X₂≥ 0.

Найти решение системы ограничений (2) Х = (х₁, х₂), такое, что целевая функция (2) будет принимать максимальное значение.

Ход решения задачи:

Для решения задачи на ПК с использованием Excel необходимо:

1. Ввести исходные данные в ячейки рабочего листа Excel.

2. Разместить блоки ячеек на рабочем листе Excel, необходимые для моделирования наиболее дешевого рациона питания, а также для формирования элементов математической модели и целевой функции.

3. Сформировать на рабочем листе Excel элементы математической модели и целевую функцию.

4. Настроить программу «Поиск решения» и выполнить ее.

Вводим исходные данные:

Размещаем блоки ячеек, необходимые для моделирования наиболее дешевого рациона питания, а также для формирования математической модели и целевой функции:

Выделяем блок ячеек «Оптимальный выпуск» (B12:C12) и заполняем их значениями 0,01

Выделяем первую ячейку «Фактически использовано» (E4), нажимаем на кнопку Автосуммирование, далее нажимаем на кнопку DELETE и выделяем блок B12:C12, нажимаем на кнопку * и выделаем блок B4:C4 (содержание питательных веществ). Нажимаем CTRL+SHIFT+ENTER.

Проделываем эту же операцию с ячейками E5:E7 соответственно.