Теория зацепления цепи со звездочкой в наиболее общем виде проявляется при исследовании зацепления круглозвенной цепи. Как известно, в процессе эксплуатации в результате износа и вытяжки звеньев шаг цепи увеличивается. В ряде случаев это приводит к такому размещению звеньев на звездочке, при котором горизонтальное звено располагается на ней, касаясь только в четырех точках (рис. 6.4). Такое положение при определенном соотношении SНб и SСб можно считать устойчивым.
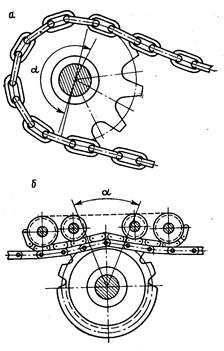
Рисунок 6.1 - Звездочные приводные устройства с неподвижным
контактом между зубом и звеном тяговой цепи
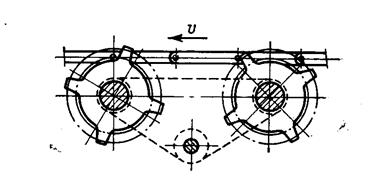
Рисунок 6.2 - Звездочное приводное устройство со скользящим контактом
между зубьями звездочки и шарнирами тяговой цепи
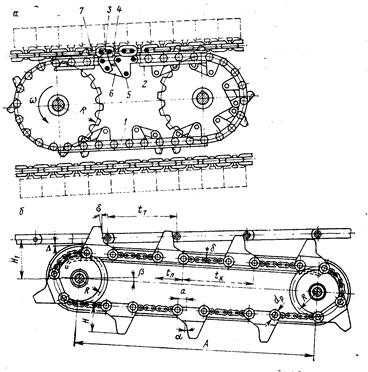
1- приводная цепь; 2 - направляющая; 3 - кулак; 4 - звено приводной цепи;
5 - звено с отливом; 6 - тяга; тяговая цепь.
Рисунок 6.3 - Гусеничные приводные устройства
Рассматривая рис. 6.4, можно видеть, что шарниры цепи при прохождении через звездочку как бы сливаются с ней. Если провести прямые через центры шарниров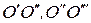 
, и т.д., то образуется звездочка, грани которой полностью совпадают с осями звеньев кольцевой цепи, расположенной на ней (рис.6.5.а, б).
При повороте такой звездочки на угол ψ перемещение тяговой цепи и (функция положения) определяется уравнением
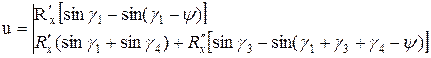
при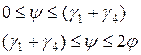 
(6.4)
где 
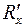и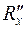 
- расстояние от центра звездочки до шарниров цепи расположенных соответственно на зубьях и ложах звездочки;
γ1 - γ4 - углы между радиусам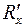и и 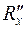и перпендикулярами к осям звеньев цепи.
При повороте звездочки на один зуб (ψ = 2φ) цепь продвигается на u =2tТ.
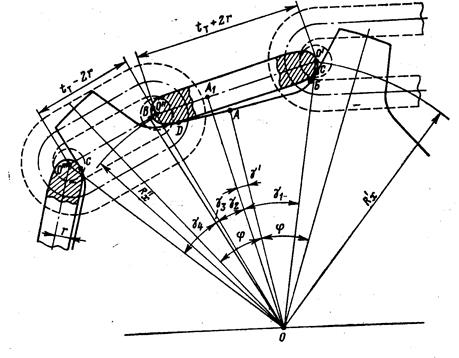
Рисунок 6.4 - Схемы размещения звеньев круглозвенной цепи на звездочке
Дифференцируя уравнение (6.4) по времени, найдем скорость перемещения элемента кольцевой цепи, расположенного у звездочки
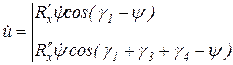при 
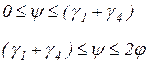(6.5)
На основании полученных уравнений построены графики изменения величины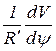 
, пропорциональной первой передаточной функции (R` - радиус начальной окружности звездочки) в зависимости от угла поворота ψ (рис.6.6). Можно видеть, что изменение первой передаточной функции возрастает с увеличением шага тяговой цепи tТ. При этом возрастание изменения происходит в первый период цикла, в то время как во втором цикле происходит снижение. С увеличением шага тяговой цепи продолжительность второго цикла сокращается и при некотором предельном значении tТ = tПред становится равным нулю. В этом случае изменение первой передаточной функции в первом цикле достигает максимальных значений. Из графика видно, что сравнительно небольшие изменения шага тяговой цепи приводят к значительным изменениям первой передаточной функции.
Круговая частота изменения первой передаточной функции (пропорциональной скорости движения тяговой цепи) определяется числом зубьев звездочки
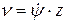, (6.6)
где z - число зубьев звездочки.
Для разборной цепи γ1 = γ4, γ2 = γ3. Тогда, подставляя в (6.4) и (6.5) соответствующие значения углов, получим формулы для смещения и скорости звена разборной цепи, расположенного у звездочки. На рис.6.6.б представлен график изменения величины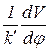 
, пропорциональной скорости 
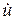для разборной цепи с номинальным шагом tТ = 80.
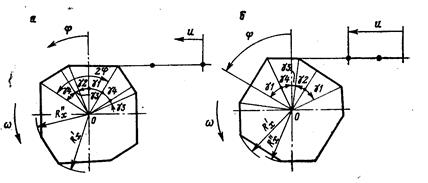
Рисунок 6.5 - Схематизация зацепления реальной системы круглозвенной
цепи со звездочкой
Для сравнения полученных результатов на рис. 6.6.б приведен график изменения первой передаточной функции (пунктирная кривая) в соответствии с уравнением
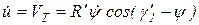, (6.7)
в котором не учитываются изменения шага тяговой цепи и отсутствие половины зубьев на реальной звездочке для разборной цепи.
Преобразованные уравнения для разборной цепи показывают, что наименьшая частота вынужденных колебаний тяговой цепи определяется равенством (6.6) и зависит от числа зубьев звездочки z, а не от числа граней, образующихся при набегании цепи на звездочку, как принималось обычно.
Амплитуда колебаний наименьшей частоты при номинальном шаге тяговой цепи незначительна, и поэтому в начальный период работы привода она не оказывает существенного влияния на колебания цепи. В процессе эксплуатации шаг тяговой цепи увеличивается, а это, в свою очередь, приводит к увеличению влияния ее на колебания тяговой цепи. Это можно проиллюстрировать, если функцию скорости (6.5) при γ1 = γ4, γ2 = γ3 разложить в ряд Фурье. Тогда
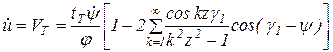, (6.8)
где k =1, 2, 3 …; 0 ≤ ψ ≤ ∞.
В (6.5) было принято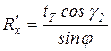 
; 
.
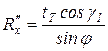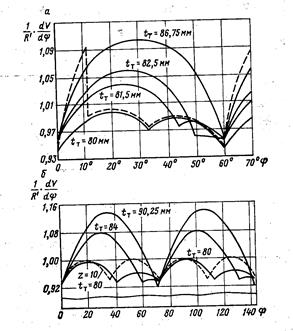
Рисунок 6.6 - Графики первой передаточной функции в зависимости от угла
поворота звездочки для круглозвенной (а) и разборной (б) цепей
Поскольку шаг тяговой цепи в связи с ее износом меняется сравнительно в небольших пределах, член, стоящий перед квадратными скобками, не оказывает значительного влияния на изменения скорости VТ. Амплитуды же отдельных гармоник зависят от угла γ1, который определяется шагом тяговой цепи tT (γ1 = φ - γ2). При сравнительно небольших изменениях tT (z = 5) угол γ1 меняется от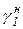 
до φ = 36º. В связи с этим амплитуды в уравнении (6.8) 
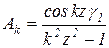меняются в весьма широких пределах.
На рис 6.7 представлен график изменения амплитуд Ak в зависимости от изменения угла γ1, из которого видно, что амплитуда первой частоты (k =1) при изменении γ1 от 18º до 36º интенсивно возрастает по абсолютной величине, а абсолютная величина амплитуды второй частоты (k = 2) вначале убывает от максимума до нуля, а затем возрастает до максимума. Следует отметить, что при γ1 = 18º, т.е. при условии, когда звенья цепи на звездочке должны размещаться по правильному многограннику (условие зацепления пластинчатой цепи со звездочкой z1 = 2z), амплитуды нечетных гармоник обращаются в нуль. Следовательно, первая частота в данном случае отсутствует, а амплитуда второй частоты максимальна и по существу определяет колебательное движение пластинчатой тяговой цепи с низшей частотой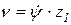 
,
где z1 - кинематическое число зубьев (граней) на звездочке.
Если принять, что в уравнении (6.8) k = 2, 4, 6, …, или, что равнозначно kz = k1z1, где k1 = 1, 2, 3,..., то после нескольких преобразований при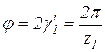 
можем записать 
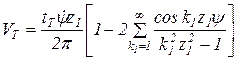. (6.9)
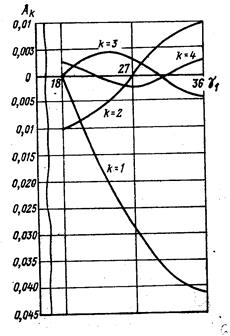
Рисунок 6.7 - График изменения амплитуд Ак в зависимости от угла γ1
Полученное уравнение является также результатом разложения в ряд Фурье зависимости скорости движения пластинчатой тяговой цепи (6.7). Как видно из уравнения (6.9), в данном случае изменение шага тяговой цепи tТ (в пределах износа цепи) не влияет на форму колебания скорости VТ и оказывает лишь незначительное влияние на ее величину.
При работе рассматриваемого приводного устройства часто возникают условия, которые обусловливают неустойчивое положение горизонтального звена на звездочке при входе в зацепление. В этом случае при некотором угле поворота звездочки ψk горизонтальное звено начинает проскальзывать по зубу, пока не опустится в ячейку звездочки. За период проскальзывания точка контакта С (рис.2.8) переходит в точку Б. Такую работу приводного устройства нельзя считать нормальной.
Тем не менее в большинстве случаев в реальных условиях в период входа в зацепление происходит проскальзывание звена по зубу звездочки.
Функции положения, соответствующие данным условиям зацепления цепи со звездочкой, определяются равенством (предполагается, что соскальзывание звена по зубу при ψ= ψк происходит мгновенно).
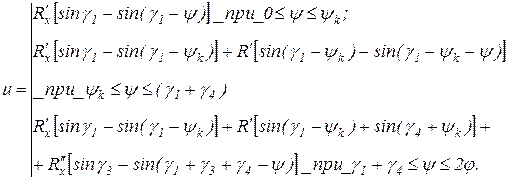(6.10)
Скорость элемента тяговой цепи, расположенного у звездочки
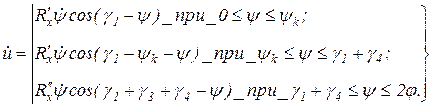(6.11)
В соответствии с уравнениями (6.11) построен график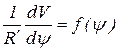 
(рис.6.6), пропорциональный скорости тяговой цепи (пунктирная кривая). Из графика можно видеть, что период изменения функции (6.11) совпадает с периодом работы приводного устройства без проскальзывания звена цепи по зубу звездочки.
