Механизмы мостовых кранов состоят из большого числа сосредоточенных и распределенных масс. Исследование движения таких систем в общем виде практически невозможно. Для изучения главных динамических процессов в механизме составляется идеализированная расчетная схема.
Чаще всего движущиеся узлы механизма представляют собой массивные и жесткие тела, которые перемещаются в течение переходного процесса почти как одно целое. Такие узлы считают абсолютно жесткими, а всю их массу предполагают сосредоточенной в точках, совпадающих с центрами тяжести. К таким «точечным массам» можно отнести груз, вращающиеся части двигателя, тормозной шкив, зубчатые колеса, барабаны и др.
Общая деформация механизма определяется главным образом упругостью валов, канатов и других элементов, имеющих малую массу. Эти элементы можно считать с известным приближением безмассовыми и абсолютно упругими.
Таким образом, расчетную схему механизма можно представить рядом точечных масс, соединенных невесомыми абсолютно упругими связями.
Если считать законы изменения внешних нагрузок, действующих на такую систему, заранее заданными и пренебречь- волновыми процессами при распространении деформаций вдоль кинематической цепи, упругой податливостью в местах сочленения кинематических пар, затуханием колебаний вследствие вязкого трения, конструкционного демпфирования и утечек энергии через опоры, изменением исходных параметров системы, то можно достаточно точно аналитически описать переходный процесс.
Зная характер изменения и величину динамических нагрузок в упругих элементах мостовых кранов, можно обоснованно проводить расчеты несущей способности, прочности и долговечности (как по выносливости, так и по износу), а также изыскивать эффективные меры повышения их надежности.
В составе каждого механизма всегда есть вращающиеся и поступательно движущиеся узлы. Для большей наглядности динамического взаимодействия отдельных масс друг с другом их располагают на одной какой-нибудь упругой связи. В таком случае говорят, что массы «приводят» к одной связи. Такая расчетная схема называется эквивалентной или приведенной расчетной схемой. Анализируя динамические процессы в такой схеме, необходимо помнить о том, что имеем дело с приведенной схемой, в которой все расчетные параметры: и нагрузки, и массы (моменты инерции, маховые моменты), и коэффициенты жесткости имеют приведенное значение.
Расчетные параметры можно приводить в любое заранее выбранное место механизма, на любой его упругий элемент.
Если приведение произведено на какой-нибудь вал механизма, то тогда получается расчетная приведенная схема вращательного движения (рис. 24, а). В такой схеме (рис. 24, б) нагрузки характеризуются крутящими моментами М, инерционные свойства масс — моментами инерции J или маховыми моментами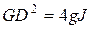 
, упругость кинематических элементов — коэффициентами жесткости при кручении Скр.
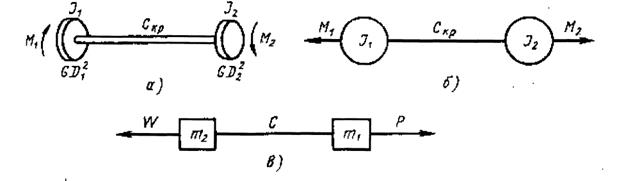
Рисунок 4.1 - Типы расчетных схем: а и б — вращательного движения;
в — поступательного движения
Если приведение произведено на какой-нибудь поступательно движущийся элемент (например, канаты, цепи, рейки, штанги и т. п.), то тогда получается расчетная приведенная схема поступательного движения (рис. 4.1, в). В такой схеме нагрузки характеризуются силами (P, T, W или F), инерционные свойства движущихся узлов — их массами m, упругость кинематических элементов — коэффициентами жесткости при растяжении или сжатии С.
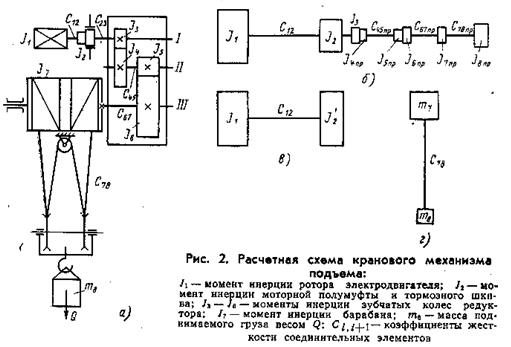
В качестве примера рассмотрим составление расчетной схемы кранового механизма подъема (рис. 4.1, а). Моменты инерции валов механизма ничтожно малы по сравнению с моментами инерции других узлов. Поэтому валы считаем безынерционными. Предположим, что приведение следует производить к валу I механизма. Тогда массы и жесткости вала приведения останутся неизменными (рис. 4.1, б), а массы и жесткости других валов будут иметь приведенные величины. Учитывая, что обычно массы J1 и J2 являются наибольшими, расчетную схему механизма можно представить в двухмассовой интерпретации вращательного движения (рис. 4.1, в):
.
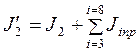Если же приведение нужно выполнить к грузу, тогда масса груза m8 и жесткость канатной подвески С78 останутся неизменными (рис. 4.1, г), а массы и жесткости всех вращающихся валов будут иметь приведенные величины. В этом случае расчетная схема механизма подъема будет представлена в двухмассовой интерпретации поступательного движения (рис. 4.1, г), где приведенная масса вращающихся частей будет
,
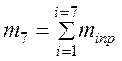а масса груза, представляющая собой основную поступательно движущуюся массу, будет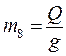 
.
Расчетные приведенные схемы вращательного и поступательного движения совершенно идентичны как по простоте приведения, так и по полученным результатам.
Однако для составления исходных уравнений движения схемы поступательного движения, как правило, более наглядны. Поэтому их применяют не только в механизмах, где есть поступательно движущиеся детали, но и тогда, когда все массы механизма имеют только вращательное движение (например, в механизмах вращения или поворота и т. п.). В этом случае (рис. 4.1, б) моменты инерции движущихся частей изображаются линейно связанным кружками, а нагрузочные моменты изображаются линейными векторами.
