ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Тема 1. Границы производственных возможностей общества.
Альтернативная стоимость.
| – А скажи мени, куме, чому колы я липлю варэники, то можу злэпыты або дэсять варэныкив з картоплею и сорок з вышнэю, або сорок з картоплею и двадцять с вышнэю? Чому так? Гроши те ж самы, а количество разно? – Це, Грыцько, треба экономику знать. Альтернативную стоимость. |
ЗАДАЧА 1
Три студента – Петро, Павло и Осип выполняют контрольные работы по физике (Y) и по математике (Х). Первый (Петро) может выполнить 6 к.р. по физике или 4 к.р. по математике, второй (Павло) – 4 к.р. по физике или 5 к.р. по математике, третий (Осип) – 8 к.р. по физике или 2 к.р. по математике. Определите, применяя категорию альтернативной стоимости (Аст), как эффективно распределить имеющиеся ресурсы на выполнение контрольных работ? Кто более производителен при выполнении работ по математике? Составьте таблицу производственных возможностей, учитывая действие закона возрастания альтернативных затрат и постройте график. При каких условиях этот закон не действует?
Решение. По условию задачи экономическим ресурсом является труд. При полном использовании ресурсов можно выполнить 18 контрольных работ по физике, тогда 0 – по математике, или 11 контрольных работ по математике, тогда 0 – по физике. Если все три студента заняты выполнением контрольных работ по физике, то перераспределять студентов на выполнение работ по математике надо с учётом их способностей (пригодности). Определим относительную пригодность ресурсов по альтернативной стоимости выполнения контрольных работ по математике для каждого студента. Наиболее пригодным для данного вида деятельности является ресурс, имеющий самую низкую альтернативную стоимость производства данного блага. Данные запишем в таблицу.
| Студенты | К.р. по физике (т. Y) | К.р. по математике (т. Х) | Аст тов. Х = -DY/+DX |
| Петро | -1,5 Y – менее пригодный | ||
| Павло | -0,8 Y –самый пригодный | ||
| Осип | -4 Y – самый непригодный | ||
| Всего: |
Составим таблицу производственных возможностей, распределяя студентов с учётом их пригодности на выполнение контрольных работ по математике – сначала Б, потом А и затем В.
| Альтернативы | К.р. по физике, Y | – DY | К.р. по математике, X | + DX | Аст доп. ед. т. Х = – DY/+DX |
| 3 студента – по физике | |||||
| 2 по физике +1 по математике | – 4 | +5 | 0,8 Y | ||
| 1 по физике +2 по математике | – 6 | +4 | 1,5 Y | ||
| 3 студента – по математике | – 8 | +2 | 4 Y |
По таблице видно, что при переходе от одной возможности к другой альтернативная стоимость каждой дополнительной контрольной работы по математике возрастает, то есть действует закон возрастания альтернативных затрат. Причина действия закона – неодинаковая пригодность ресурсов для производства альтернативных благ. Сначала используется самый пригодный ресурс, для которого характерны самые низкие альтернативные издержки (альтернативная стоимость), затем используется менее пригодный ресурс и т.д. Соответственно, упущенные возможности (отказ от производства альтернативных товаров) возрастают.
По данным таблицы построим график производственных возможностей. График выглядит как линия выпуклая от начала координат, что означает увеличение угла наклона к горизонтальной оси или, с экономической точки зрения, возрастание альтернативной стоимости (альтернативных затрат) дополнительных единиц т. Х (к.р. по математике). Закон не действует в том случае, если ресурсы обладают одинаковой производительностью. Тогда альтернативная стоимость всех дополнительных единиц блага одинакова. График будет выглядеть как прямая нисходящая линия.
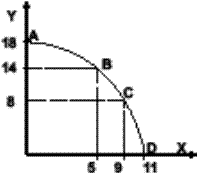
Рис. 15 Кривая производственных возможностей
ЗАДАЧА 2
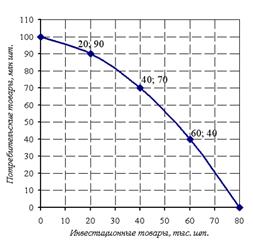
Экономика некоторой страны находится на границе своих производственных возможностей, которые отражены на графике:
Текущая ситуация: производится 60 тыс. шт. инвестиционных товаров и 40 млн шт. потребительских товаров. Альтернативная стоимость решения об увеличении производства дополнительных единиц потребительских товаров на 50 млн шт. равна ____ тыс. шт. инвестиционных товаров.

| 
| 0,8 | 
| ||

| 1,25 | 
|
Решение:
Величину экономического эффекта X (инвестиционных товаров), которой пришлось пожертвовать ради прироста иного экономического эффекта Y (потребительских товаров), принято называть альтернативной стоимостью эффекта Y:  .
.
ЗАДАЧА 3
Программист Иванова зарабатывает в час 45 рублей. В магазине за продуктовыми наборами по 40 руб./кг нужно стоять час, по 60 руб./кг очередь отсутствует. При каком объёме покупок рационально приобретение более дешёвых наборов для программиста Ивановой? Для безработного, получающего пособие?
Решение. Данная задача показывает альтернативную ценность времени, проведенного в очереди. Альтернативная стоимость времени для безработного равна нулю, в этом случае рациональный выбор – простоять час в очереди. Альтернативная стоимость времени программиста Ивановой – 45рублей в час. Цена покупки для неё должна быть меньше по сравнению с ценой покупки без очереди:  , где X – объём покупки в кг. Решаем неравенство:
, где X – объём покупки в кг. Решаем неравенство:
40 X + 45 < 60 X
45 < 20 X
2,25 < X
X > 2,25
Итак, для программиста Ивановой постоять в очереди рационально только при покупке продуктов больше 2,25 кг.
ЗАДАЧА 4
В таблице 1 приведены данные об изменении структуры производства в стране А в условных единицах.
| Варианты | A | B | C | D | E | F | G | H |
| Машины | ||||||||
| Хлеб.издел. |
Рассчитать альтернативные издержки производства единицы хлебобулочных изделий.
Решение:
При переходе из точки А в точку В будет производится 10 ед. хлебобулочных изделий, для этого необходимо отказаться от производства 1 ед. машины. Альтернативные издержки производства единицы хлебобулочных изделий составят (7-6 /10-0), т.е. 1/10.
При переходе из точки В в точку С будет производится 19 ед. хлебобулочных изделий, для этого необходимо отказаться от производства 1 ед. машин. Альтернативные издержки производства единицы хлебобулочных изделий составят (6-5/19-10), т.е. 1/9.
При переходе из точки С в точку D будет производится 27 ед. хлебобулочных изделий, для этого необходимо отказаться от производства 1ед. машины. Альтернативные издержки производства единицы хлебобулочных изделий составят (5-4/27-19), т.е. 1/8.
При переходе из точки D в точку E будет производится 34 ед. хлебобулочных изделий, но необходимо отказаться от производства 1 ед. машины. Альтернативные издержки производства единицы хлебобулочных изделий составят (4-3 /34-27), т.е. 1/7.
При переходе из точки E в точку F будет производится 40 ед. хлебобулочных изделий, но необходимо отказаться от производства 1 ед. машины. Альтернативные издержки производства единицы хлебобулочных изделий составят (3-2/40-34), т.е. 1/6.
При переходе из точки F в точку G будет производится 45 ед. хлебобулочных изделий, но необходимо отказаться от производства 1 ед. машины. Альтернативные издержки производства единицы хлебобулочных изделий составят (2-1/45-40), т.е. 1/5.
При переходе из точки G в точку H будет производится 49 ед. хлебобулочных изделий, но необходимо отказаться от производства 1 ед. машины. Альтернативные издержки производства единицы хлебобулочных изделий составят (1-0/49-45), т.е. 1/4.
Альтернативные издержки производства единицы хлебобулочных изделий возрастают по мере увеличения выпуска за счёт отказа ресурсов производства машин.
Тема 2. Основы теории спроса и предложения. Рыночное равновесие. Эластичность спроса и предложения
| – Мыкола, скажи мени, ось у тому мисяци ходыв я на ярмарок с десятью карбованцями, та купыв на пять карбованцив кило сала и на пять – торбу сэмечек. Сегодни пийшов – всё здорожало. Сала я також купыв кило, тильки вже за семь карбованцив, а сэмечков – тильки пив-торбы. А их я не меньше сала люблю. Чому ж я сала стольки ж купыв, а сэмечек меньше? – Грыцько, тут вся справа в эластичности. Колы сало неэластично по цене, то скильки б воно не стоило – всё одно купышь... |
ЗАДАЧА 1
Спрос и предложение на обеды в столовой описываются уравнениями:
QD = 2400 – 10 P,
QS = 1000 + 25 P,
где P – цена обеда (в рублях),
Q – количество обедов в день.
– Рассчитайте равновесную цену и количество проданных обедов.
– Если администрация установит цену в 30 руб. за обед, то каковы будут последствия такого решения?
Решение:
Равновесная цена – цена, уравновешивающая спрос и предложение в результате действия конкурентных сил. Приравняем объём спроса и объём предложения и решаем уравнение.
QD = QS
2400 – 10 P = 1000 + 25 P
2400-1000=25 Р + 10 Р
1400=35 Р
Р = 40 рублей.
Количество проданных обедов – это равновесное количество обедов, которе можно определить, подставив в любое уравнение значение цены.
QD = 2400 – 10 P = 2400 – 10 . 40 = 2000 обедов
Если цена будет установлена администрацией 30 руб., то объём предложения составит: 1000 + 25 . 30 = 1750 обедов в день, а объём спроса
QD = 2400 – 10 . 30 = 2100 обедов в день, т.е. спрос больше на 2100 – 1750 = 350 обедов, чем предложение.
ЗАДАЧА 2
Функция спроса на данный товар имеет вид QD = 80 – 5 P. Функция предложения данного товара QS = 30 + 5 P. Правительство установило налог, уплачиваемый продавцом, в размере 2$ за единицу товара. Определите равновесную цену (с налогом и без налога) и равновесный объём продаж. Постройте график. Определите, как распределяется налоговое бремя между продавцами и покупателями и величину избыточного налогового бремени (потеря эффективности для общества). См. К. Макконнелл, С. Брю. Экономикс, 1992 г, т. 2, гл. 33, стр. 207.
Решение. Определим равновесную цену и равновесное количество до налогообложения, приравнивая функции QD = QS:
80 – 5 P = 30 + 5 P
P = 5; QD = QS = 55.
Представим равновесие с учётом данных функций графически.
Государство вводит товарный налог на продавца t = 2 $ Новая цена предложения, учитывающая налог, P t и цена до введения налога P, очевидно связаны между собой следующим образом: P = Pt – t. Для определения функции предложения после введения налога необходимо заменить в исходном уравнении P на (Pt – t). Тогда функция предложения будет иметь вид:
QS = 30 + 5(Pt – t) = 30 + 5 Pt – 5 t = 30 + 5 Pt – 5 . 2 = 30 + 5 Pt – 10 = 20+5 Pt.
Согласно этой функции, предложение сократится, то есть график предложения сместится вверх на 2$ и влево по горизонтали на 10 единиц. Функция спроса не изменится. Определим новое равновесие:
80 – 5 P = 20+5 Pt PD = Pst = 6; QD = QS = 50.

Цена S1 S
P D
Потери
Покупателей
Потери
Продавцов
20 30 50 55 80 Q
Рис. 16 Смещение рыночного равновесия
Таким образом, равновесное количество покупаемой продукции сократилось и цена повысилась. Обратите внимание, что цена возросла на меньшую величину, чем налог, в результате действия механизма рынка. Объём налоговых поступлений от поступления товарного налога равен произведению величины налога на продаваемое количество товара:
T = t . Qet = 2 . 50 = 100.
Установление налога ведёт к потерям и для продавцов и для покупателей. Потери покупателей. Ранее объём 50 потребители покупали по цене 5$ Их расходы были равны 50 . 5 = 250$ Теперь они за этот объём платят 50 . 6 = 300$. Их потери составляют 50$.
Потери продавцов. Ранее продавцы продавали объём 50 по цене 5$ и получали доход 250$. Теперь они получают доход 300$ от продажи 50 единиц по цене 6$. Казалось бы, их доходы возросли. Но с каждой проданной единицы продавцы должны заплатить 2$, то есть общую сумму 100$ В результате реальная цена продажи для них составит 4$, и их фактический доход от продажи 50 единиц составит 200$, что на 50$меньше, чем до введения налога (это их потери).
В данном примере налоговое бремя распределилось одинаково, что следует из расчётов и видно по графику. Это связано с одинаковой эластичностью спроса и предложения (что показывает коэффициент при независимой переменной в функции спроса и предложения). Если эластичность спроса более высокая, то налоговое бремя в основном падает на продавцов. Если эластичность предложения более высокая, то налоговое бремя падает в большей степени на покупателей.
На графике потери эффективности для общества показаны заштрихованным треугольником. Это тот объём продукции, который не был произведен и его не смогли приобрести покупатели, и тот объём доходов, который не получили продавцы.
ЗАДАЧА 3
Используя приведенные в таблице данные, рассчитать коэффициент эластичности и выручку.
| Цена товара Р (в руб.) | ||||
| Объём спроса Q(штук) |
Решение:
Выручка (TR) определяется: TR= P  Q,
Q,
где P –цена товара,
Q– объём спроса.
Подставляем данные из таблицы и определяем выручку:
1) TR= P  Q= 180
Q= 180  200 = 36000 руб.
200 = 36000 руб.
2) TR= P  Q= 150
Q= 150  300 = 45000 руб.
300 = 45000 руб.
3) TR= P  Q= 120
Q= 120  400 = 48000 руб.
400 = 48000 руб.
4) TR= P  Q= 90
Q= 90  500 = 45000 руб.
500 = 45000 руб.
Коэффициент эластичности определяем по формуле:
К эл. =  ,
,  (коэффициент дуговой эластичности).
(коэффициент дуговой эластичности).
Кэл.=  =
=
= 
Кэл.=  =
=
= 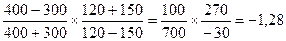
Кэл.=  =
=
= 
Коэффициент ценовой эластичности представляет собой отрицательную величину, но во внимание принимается лишь абсолютное значение. В зависимости от величины коэффициента различают спрос эластичный (2,2),(1,28), то есть больше 1, единичной эластичности (1), спрос неэластичный (0,78), т.е. меньше 1. Ценовая эластичность спроса влияет на общий объём выручки от продажи данного количества товаров.
При эластичном спросе (коэффициент 2,2) выручка увеличивается на (45000-36000) 9000 руб.
При эластичном спросе (коэффициент 1,28) выручка увеличивается на (48000-45000) 3000 руб.
При неэластичном спросе (коэффициент0,78) выручка уменьшается на (45000-48000) – 3000 руб.
ЗАДАЧА 4
Величина спроса на фрукты задана уравнением QD = 20 – 2 P, величина предложения QS = 2 + P.
1) Определите равновесную цену и объём продаж аналитически, по графику и по таблице.
2) На основе данной функции спроса определите, как изменяется эластичность спроса при снижении цены – по показателю общей выручки.
3) Определите, достигается ли при данном равновесном количестве максимальная выручка?
4) Как изменится выручка продавца, если предложение возрастет на 3 единицы? на 5 единиц?
5) Рассчитайте эластичность спроса по коэффициенту эластичности (дуговой и точечной).
Решение. 1) Равновесная цена – цена, уравновешивающая спрос и предложение в результате действия конкурентных сил. В условиях равновесия величина спроса равна величине предложения, цена спроса равна цене предложения. Для аналитического решения приравняем функцию спроса и функцию предложения и найдем равновесную цену:
QD = QS 20 – 2 P = 2 + P 20 – 2 = 2 Р + Р
18 = 3 P
Р = 6 рублей.
Подставим значение цены в функцию спроса или в функцию предложения и определим равновесное количество QD = QS = 8 единиц.
Графически равновесие – это точка пересечения графиков спроса и предложения. Отметим по вертикальной оси значения цены, по горизонтальной оси – количество продукции и построим графики спроса и предложения по данным линейным функциям. График спроса будет выглядеть как прямая нисходящая линия. Крайние точки – это цена P = 10, при которой величина спроса QD = 0, и количество QD = 20 при цене P = 0. Кроме того, отмечаем точку равновесия P = 6, QD = 8. График предложения выглядит как прямая восходящая линия. Для построения отмечаем точку на горизонтальной оси – величину предложения QS = 2 при цене P = 0 и равновесную точку P = 6, QS = 8. Графики пересекаются в точке равновесия.

Рис. 17 Рыночное равновесие
Для решения в табличной форме необходимо заполнить таблицу, отмечая в ней изменение величины спроса QD и величины предложения QS при изменении (снижении) цены. В таблице принято указывать изменение цены, начиная от максимальной до P = 0. Максимально высокая цена – это цена, при которой величина спроса QD = 0. Соответственно, при нулевой цене величина спроса максимальна. По функции спроса находим, что величина спроса QD = 0, когда P = 10. Далее, на каждую единицу снижения цены величина спроса возрастает на 2 единицы, в соответствии с коэффициентом при независимой переменной (цене). При цене P = 0 величина спроса QD = 20 (max). Величина предложения при снижении цены на одну единицу снижается с учётом коэффициента, данного в функции, также на одну единицу.
При цене P = 6 руб. установится равновесие, то есть величина спроса равна величине предложения QD = QS = 8 единиц.
| Цена P, руб. | Величина спроса QD, ед. | Величина предложения QS ед. | Величина предложения | Общая выручка TR = P . Q | Коэффициент эластичности спроса ED | ||
| QS +3 ед. | QS +6 ед. | ∆Q %/ ∆P % | ∆Q/∆P . P / Q | ||||
| ∞ | |||||||
| 5,7 | ... | ||||||
| ... | ... | ||||||
| 6 | 8 | 8 | 1,85 | 1,5 | |||
| 1,2 | |||||||
| 0,8 | ... | ||||||
| ... | ... | ||||||
| ... | ... | ||||||
| ... | 0,1 | ||||||
| 0,05 |
2) Эластичность спроса – степень реакции потребителей на изменение цены.Эластичность спроса при линейной функции спроса не остаётся постоянной величиной. При последовательном снижении цены и движении по графику спроса вниз, эластичность спроса снижается, спрос из эластичного превращается в неэластичный.
Эластичность спроса можно определить по общей выручке TR = P . Q. Если при снижении цены TR растет, то спрос эластичный, снижать цену и увеличивать производство выгодно. Если при снижении цены TR снижается, то спрос неэластичный. Внесем показатели общей выручки TR в таблицу.
3) По таблице видно, что равновесие достигается на участке эластичного спроса, но выручка при данной функции спроса TR = P . Q = 6 . 8 = 48 не максимальна, то есть возможно дальнейшее снижение цены.
4) Если под влиянием неценовых факторов предложение возрастет на 3 единицы, функция предложения будет иметь вид QS = 5 + P и сместится по горизонтали на 3 единицы вниз вправо. Новые значения величины предложения внесем в таблицу. Определим новое равновесие аналитически и по таблице. В результате действия рыночного механизма цена снизится до 5 руб., объём продаж составит 10 ед., выручка TR = P . Q = 5 . 10 = 50 возрастет и будет максимальна. Если предложение возрастет на 6ед., цена снизится до 4 руб., но выручка TR = P . Q = 4 . 6 = 48 сократится, поскольку спрос стал неэластичным.
Объём, при котором выручка максимальна, можно определить аналитически. Известно, что в точке экстремума (минимальных или максимальных значений функции) производная от этой функции равна нулю. На основе функции спроса можно составить функцию общей выручки TR = P . QD. Преобразуем функцию спроса в функцию цены, то есть QD = 20 – 2 P, отсюда P = 10 – 0,5 QD.
Тогда общая выручка TR = (10 – 0,5 QD) . QD = 10 QD – 0,5 QD 2.
В точке максимума производная выручки TR΄ = MR = 0.
TR ΄ = (10 QD – 0,5 QD 2)΄ = 10 – QD = 0. Отсюда QD = 10, соответственно P = 5.
При объёме 10 ед. и цене 5 руб. выручка достигает максимального значения, соответственно коэффициент эластичности при этом объёме будет равен ED = 1. Дальнейшее снижение цены приведет к снижению выручки, а значит, спрос станет неэластичным, и коэффициент эластичности будет меньше единицы.
5) Эластичность спроса можно определить по коэффициенту эластичности. Обычно для расчёта используется коэффициент дуговой эластичности, который применим к небольшим интервалам изменения цены и количества:
 ;
;
где ∆Q (%) – относительное изменение объёма спроса;
∆P (%) – относительное изменение цены товара.
В этой формуле в качестве основания берется либо первое, либо второе значение цены и количества.
Более точным является расчёт коэффициента эластичности по методу центральной точки, где за основание берем среднюю величину количества и среднюю величину цены:
 , или после преобразований:
, или после преобразований:
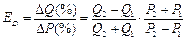 , или
, или  ;
;
Например, при снижении цены:
– от10 руб. до 9 руб.:
ED = (2 – 0)/(2 + 0) . (10 + 9)/(10 – 9) = 1 . 19 = 19 > 1 – эластичный спрос. → ∞
– от 9 руб. до 8 руб.:
ED = (4 – 2)/(4 + 2) . (9 + 8)/(9 – 8) = 1/3 . 17/1 = 5,7 > 1 – эластичный спрос. → ∞
– от 7 руб. до 6 руб.:
ED = (8 – 6)/(8 + 6) . (7+6)/(7 – 6) = 1/7 . 13/1 = 1,85 > 1– эластичный спрос.
– от 6 руб. до 5 руб.:
ED = (10 – 8)/(10 + 8) . (6+5)/(6 – 5) = 1/9 . 11/1 = 1,2 →1 – единичная эластичность.
– от 5 руб. до 4 руб.:
ED = (12 – 10)/(12+10) . (5+4)/(5 – 4) = 1/11 . 9/1 = 0,8 < 1 –неэластичный спрос.
– от 1 руб. до 0 руб.:
ED = (20 – 18)/(20 + 18) . (1 + 0)/(1 – 0) = 1/19 . 1 = 0,05 → 0 абсолютно неэластичный спрос.
Если график спроса задается линейной функцией QD = a – bP, то можно определить эластичность спроса в каждой точке на графике, то есть при каждом сочетании цены и количества, применяя коэффициент точечнойэластичности. Коэффициент выводится из предыдущей формулы:
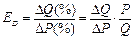 ;
;
Показатель –b при независимой переменной (цене) характеризует наклон графика спроса, совпадающий с наклоном касательной во всех точках на кривой спроса и равен -b = ∆Q/∆P. Поэтому в формуле эластичности показатель ∆Q/∆P можно заменить на –b, заданный в функции спроса. Тогда формула для расчёта точечной эластичности имеет вид:
 ;
;
где b – наклон кривой спроса.
В нашем примере в функции спроса QD = 20 – 2 P наклон равен ∆Q/∆P = – 2,коэффициент точечной эластичности
 ;
;
нак «минус» говорит только об обратной зависимости между величиной спроса и ценой, поэтому при расчётах коэффициента его игнорируют.
Посчитаем коэффициент точечной эластичности:
P = 10, Q = 0:
ED = 2 . 10/0 = ∞ – эластичный спрос;
P = 9, Q = 2:
ED = 2 . 9/2 = 9 > 1 – эластичный спрос;
P = 6, Q = 8:
ED = 2 . 6/8 = 1,5 > 1 – эластичный спрос;
P = 5, Q = 10:
ED = 2 . 5/10 = 1 – единичная эластичность.
P = 1, Q = 18:
ED = 2 . 1/18 = 0,1 < 1 – неэластичный спрос.
P = 0, Q = 20:
ED = 2 . 0/20 = 0 – абсолютно неэластичный спрос.
Коэффициент точечной эластичности выражает такую же динамику изменения выручки и эластичности спроса, что и коэффициент дуговой эластичности.
ЗАДАЧА 5
Если коэффициент эластичности товара Х по цене составляет 2, что произойдет с объёмом спроса при снижении цены с 30 до 20 рублей за единицу товара? Выгодно ли снижение цены?
Решение. По условию задачи коэффициент эластичности равен:
 ;
;
где ∆Q (%) – относительное изменение объёма спроса;
∆P (%) – относительное изменение цены товара.
Определим относительное (процентное) снижение цены товара:
∆P (%) = (20 – 30):(20 + 30)/2 = 10:25 = 0,4 = 40% ↓ (снижение).
При снижение цены объём спроса возрастает. Определим из формулы увеличение объёма спроса на данный товар:
∆Q (%) = ED . ∆P = 2 . 40% = 80% ↑ (возрастает)
Поскольку коэффициент эластичности ED = 2 > 1, спрос эластичный. Объём спроса возрастает в большей степени, чем снизилась цена, и выручка TR = P*Q возрастает, значит, снижение цены выгодно.
ЗАДАЧА 6
При доходе 5000 рублей в месяц семья потребляет 400 единиц товара Х. Эластичность спроса по доходу составляет – 0,3. Сколько единиц товара Х будет потреблять домохозяйство, если доход возрастёт на 7%?
Решение. Коэффициент эластичности со знаком минус означает, что при увеличении дохода, спрос на данный товар сокращается. Речь идёт о товарах низшей категории. Применяя коэффициент эластичности, определим, насколько сократится объём спроса на данный товар (в процентах):
 ;
;
где ∆Q (%) – относительное изменение объёма спроса;
∆I (%) – относительное изменение дохода.
∆Q (%) = EI . ∆I (%) = – 0,3 . 7% = – 2,1% ↑
2,1% от 400 составит 8,4 единиц товара Х. Следовательно, семья уменьшит потребление данного товара и будет потреблять (400 – 8,4) = 391,6 ед. товара Х.






