Кинематические характеристики механизмов

 

Звенья функционирующего механизма выполняют определенные движения. Для изучения этих движений необходимо знать их характеристики, называемые кинематическими. К кинематическим характеристикам относятся траектории точек, перемещения точек и звеньев, их скорости и ускорения и др. общем случае кинематические характеристики зависят от закона движения ведущего звена и строения механизма. Такие характеристики, как функция поло­жения, передаточная функция определяются только строением механизма.

Всякое подвижное звено механизма - это заданной формы твердое тело, точки которого и звено в целом совершают определенные движения. Следо­вательно, для нахождения кинематических характеристик движения звеньев механизма необходимо знать общие методы кинематического исследования движения материальных точек и твердых тел.

 

 

Способы задания движения точки

Существуют три способа задания движения точки: векторный, координатный и естественный.

Векторный способ задания движения точки. Векторный способ задания движения точки применяют при теоретическом рассмотрении. Положение точки в пространстве при векторном способе определяется радиус- вектором r (рис. 2.1).

Рис 2.1

Непрерывная кривая АМВ. описываемая с те­чением времени движущейся точкой /V/. называется траекторией. В зависимости от траектории дви­жение может быть прямолинейным или криволинейным.

Геометрическое место концов любого пере­менного вектора при неизменном положении его начала называется годографом. Следовательно, траектория точки совпадает с годографом ее ради­ус-вектора.

При движении точки М вектор rизменяется как по модулю, так и по направлению, другими словами, он является переменным вектором, зависящим от аргумента t

г = r (t). (2.1)

Это и есть уравнение движения точки в векторной форме.

Если в момент времени t точка находится в положении М, то в момент времени t1 = t +D t она будет находиться в положении М1Соответственно, положение точки определяется радиус-векторами rи r 1,. Вектор MM1, является вектором перемещения точки М за данный промежуток времени D t

 

MM1 = D r = r1 – r (2.2)

Отношение вектора перемещения точки к соответствующему промежут­ку времени определяет среднюю скорость точки у_ср:

(2.3)

 

Чтобы получить характеристику движения, не зависящую от выбора промежутка времени, вводится понятие скорости точки в данный момент времени:

(2.4)

Следовательно,

(2.5)

Вектор скорости точки (см. рис. 2.1) будет направлен по касательной к траектории движения точки.

Если выбрать в пространстве точку и туда перенести все векторы скоростей в моменты времени, близко отстоящие один от другого, то получим кривую, являющуюся годографом вектора скорости (рис. 2.2). Годограф скорости представляет собой геометрическое место концов вектора скорости движущейся точки.

Если за время D t скорость изменилась на величину D v, то отношение изменения скорости к промежутку времени, за который произошло это изменение, будет средним ускорением. Для нахождения значения ускорения в данный момент времени необходимо найти предел отношения приращения скорости к промежутку времени, в течение которого оно произошло, при стремлении по­следнего к нулю:

(2.6)

Таким образом,

(2.7)

 

Рис. 2.2

Координатный способ задания движения точки. Координатный метод изучения движения точки используется в основном при решении технических задач.

При движении точки ее координаты изменяются с течением времени. Следовательно:

(2.8)

Это и есть уравнения движения точки в прямоугольных координатах.

Одновременно эти уравнения являются уравнениями траектории точки в параметрической форме. Ис­ключив из них параметр /, получим уравнение траектории, характери­зующее пространственную кривую в координатной форме.

Рис. 2.3

Радиус-вектор г (рис. 2.3), определяющий положение точки М, можно представить в форме

(2.9)

где i, j, k — единичные векторы (орты).

Система осей Охуz предполагается неподвижной, вследствие чего векторы (орты) i, j, k являются постоянными. Дифференцируя выражение (2.10) для радиус-вектора г, получим

(2.10)

Выражение (2.10) представим в виде

(2.11)

где vx, vy, vz- — проекции вектора скорости на соответствующие оси координат, определяемые из выражений

(2.12)

Модуль вектора скорости определяется выражением

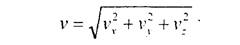(2.13)

а направляющие косинусы для вектора скорости записываются виде

(2.14)

Аналогично записываются выражения для вектора ускорения при координатном способе задания движения точки, модуля вектора и направляющих косинусов