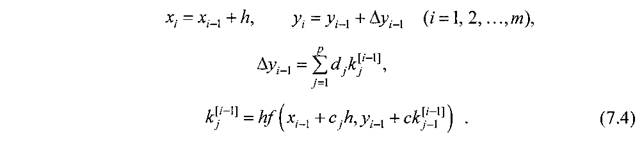В основе методологии построения математических моделей стохастических процессов и зависимостей, отражающих взаимосвязи между экспериментальными данными, лежит теория случайных величин и регрессионный анализ.
Определение 5.2. Выборочной совокупностью (или выборкой) называется совокупность случайно отобранных однородных объектов. Генеральной совокупностью называется совокупность всех однородных объектов, из которых производится выборка. Объемом совокупности (выборочной или генеральной) называется число объектов этой совокупности.
Выборка называется репрезентативной (представительной), если она достаточно хорошо представляет количественные соотношения генеральной совокупности.

Для наглядности статистическое распределение дискретной случайной величины иллюстрируется полигоном распределения. Для этого последовательные точки (х 1; w 1), (х 2; w 2), …, (хl; wl) изображают на координатной плоскости и соединяют их прямолинейными отрезками. Необходимо отметить, что точки, не являющиеся вершинами полигона, не представляют интереса с точки зрения математической статистики.
Для иллюстрации распределения непрерывной случайной величины пользуются диаграммами, которые называются гистограммами.
Гистограмма устанавливает зависимость частот от разрядов интервалов, в которые попадают значения случайной величины.
Пусть непрерывная случайная величина Х определена таблицей:

При больших объемах выборки гистограмма дает приближенное геометрическое представление о кривой распределения (графике плотности вероятности) генеральной совокупности.
Лекция 6. Понятие о численных методах решения алгебраических и дифференциальных уравнений
План лекции
1. Метод половинного деления.
2. Итерационные методы.
3. Метод Ньютона.
 Метод половинного деления для уравнения f (х) = 0
Метод половинного деления для уравнения f (х) = 0
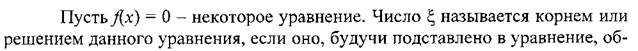


 Метод итераций для одного уравнения с одним неизвестным
Метод итераций для одного уравнения с одним неизвестным

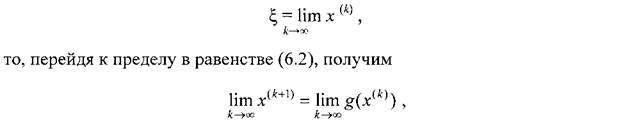

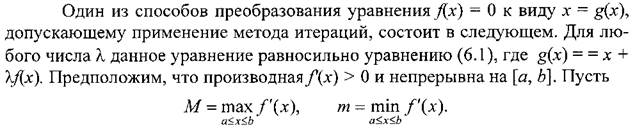

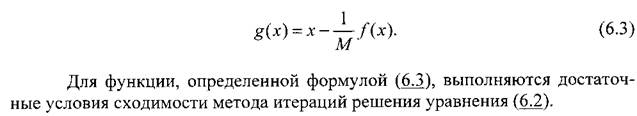

Метод Ньютона




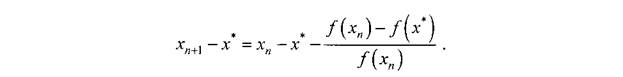


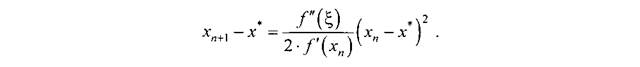
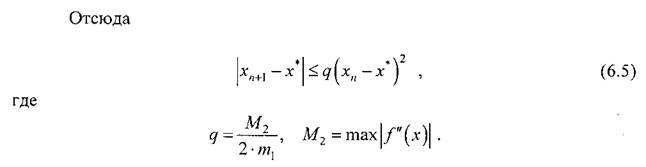
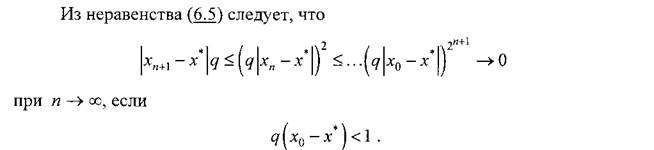

Лекция 7. понятие о Численных методах решения алгебраических
И дифференциальных уравнений
 План лекции
План лекции
Методы решения дифференциальных уравнений 


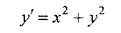


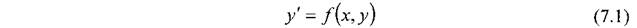
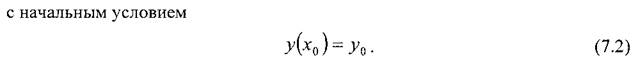












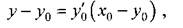
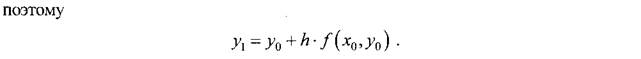
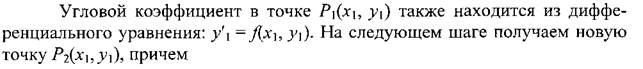
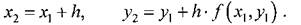

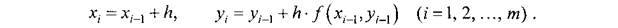

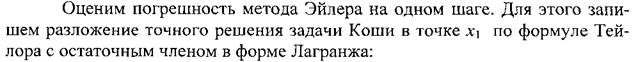
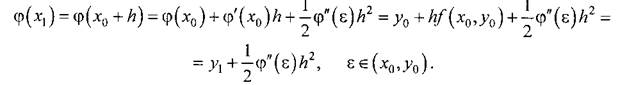
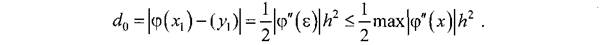
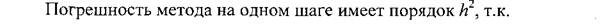

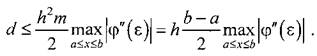


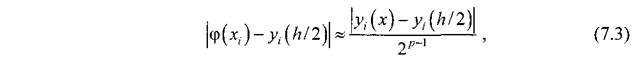




Методы Рунге–Кутта