Пусть имеется табулированная функция yi = f (xi). Введем понятие разделенной разности.
Разделенные разности нулевого порядка совпадают со значениями самой функции.
Разделенные разности первого порядка записываются следующим об-разом:
Разность Pn (x, x 0) – Pn (x 0, x 1) обращается в нуль при x = x 1, поэтому разделенная разность второго порядка
является многочленом степени n – 2. Аналогично, Pn (x, x 0, x 1, x 2) – многочлен степени n – 3 и т.д.
Разделенная разность Pn (x, x 0, x 1, …, xn- 1) порядка n – многочлен нулевой степени.
Разделенные разности более высокого порядка обращаются в нуль.
Значение Pn (x, x 0, x 1, …, xn– 1) от x не зависит, поэтому
Pn (x, x 0, x 1,…, xn- 1) = Pn (x 0, x 1, …, xn).
Из определения разделенных разностей следует
Pn (x) = Pn (x 0) + (x – x 0) Pn (x, x 0),
Pn (x, x 0) = Pn (x 1, x 0) + (x – x 1) Pn (x, x 0, x 1)
и т.д. Отсюда формула для Pn (x) имеет вид
Pn (x) = Pn (x 0) + (x – x 0) Pn (x 0, x 1) + (x – x 0) (x – x 1) Pn (x 0, x 1, x 2) +
+ (x – x 0) (x – x 1) … (x – xn- 1) Pn (x 0, …, xn). (5.2)
Разделенные разности в соответствии с рекуррентной формулой (5.1) выражаются через значения многочлена в узлах x 0, x 1, …, xn. Если x 0, x 1, …, xn узлы интерполяции, y 0, y 1, …, yn – значения интерполируемой функции в этих узлах, то они однозначно определяют интерполяционный многочлен степени n, значения которого в узлах совпадают с yi. Тогда разделенные разности многочлена Pn (x) совпадают с разделенными разностями функции f (x).
Поэтому интерполяционный многочлен можно записать в форме
Эта форма называется интерполяционным многочленом Ньютона с разделенными разностями.
Многочлен Лагранжа
Пусть задана функция y = f (x). Часто нахождение значений этой функции может оказаться трудоемкой задачей. Например, x – параметр в сложной задаче, после решения которой определяется значение f (x) или f (x) измеряется в дорогостоящем эксперименте. В этих случаях можно получить небольшую таблицу значений функции, но прямое нахождение ее значений при большом количестве значений аргумента нереально. В такой ситуации f (x) заменяется приближенной формулой g (x), которая в определенном смысле близка к функции f (x). Близость обеспечивается введением в функцию g (x) свободных параметров и их соответствующим выбором.
Итак, пусть известны значения функции f (x) в точках x 0, x 1, …, xn,
yi = f (xi), i = 0, …, n, и для некоторой функции g (x, a 0, a 1, …, an) выполняются равенства
g (xi, a 0, a 1, …, an) = yi, i = 0, 1, …, n. (5.4)
Если выражение (5.4) рассматривать как систему уравнений для определения a 0, a 1, …, an, то этот способ называется интерполяцией (лагранжвой).
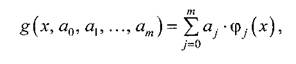Если g зависит от aj нелинейно, то говорят о нелинейной интерполяции. В противном случае интерполяция называется линейной. Для линейной интерполяции можно записать
(5.5)
где ϕ j (x) – система линейно независимых функций.
Подставим выражение (5.5) в равенство (5.4). Относительно aj получаем линейную систему уравнений:
(5.6)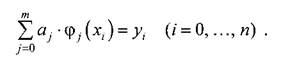 
Для однозначной разрешимости системы должно быть m = n.
Для того чтобы задача интерполирования имела единственное решение, система функций ϕ j (x) должна удовлетворять условию
(5.7)
Система функций, удовлетворяющая условию (5.7), называется
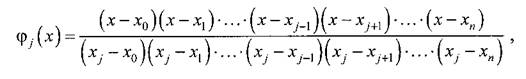чебышевской. Если ϕ j (x) задаются в виде
то формула (5.5) называется интерполяционным многочленом Лагранжа.
Многочлены Чебышева
Пусть x ∈[–1, 1]. Рассмотрим функцию вида
Tn (x) = cos[ n∙ arccos(x)]. (5.8)
Очевидно, что T 0(x) = 1, T 1(x) = x. При n = 2 используем тригонометрическое
тождество
T 2(x) = cos(2arccos(x)) = cos 2 (arccos(x)) − sin2(arcсos(x)) =
= 2cos 2 (arccos(x)) − 1 = −1 + 2 x 2.
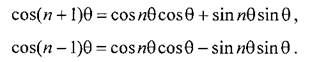Пусть Tn (x) – многочлен степени n. Получим рекуррентное соотношение, связывающее Tn –1(x), Tn (x) и Tn +1(x). Как известно,
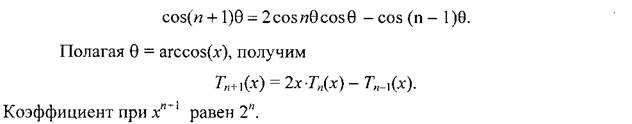Сложив почленно эти равенства, будем иметь
