Решения
Задача 1.
Граната, брошенная вертикально вверх, в верхней точке разорвалась на множество одинаковых осколков летящих с одинаковыми скоростями 20 м/с. Определить интервал времени, в течение которого осколки падали на землю.
(10 баллов)
| Возможное решение | |
Пусть t1 (t2) - время движения осколка летящего вертикально вниз (вертикально вверх). Запишем уравнения движения осколков:
0 = Н - ʋ0 t1 - 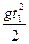 (1); 0 = Н + ʋ0 t2 - (1); 0 = Н + ʋ0 t2 -  (2)
Анализ движения осколков приводит к выводу: раньше всех упадёт на землю осколок, летящий вертикально вниз (t1). Большее время затратит на падение осколок, летящий t2. Тогда искомое время Δt=t2 - t1 ; Решая совместно уравнения (1) и (2), получаем: Δt=t2 - t1 = 4 с. (2)
Анализ движения осколков приводит к выводу: раньше всех упадёт на землю осколок, летящий вертикально вниз (t1). Большее время затратит на падение осколок, летящий t2. Тогда искомое время Δt=t2 - t1 ; Решая совместно уравнения (1) и (2), получаем: Δt=t2 - t1 = 4 с.
| |
| Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы:
описаны все вновь вводимые в решении буквенные обозначения физических величин (время движения осколков, интервал времени);
представлено полное верное объяснение с указанием наблюдаемых явлений и законов:
записаны уравнения движения осколков движения в общем виде
для первого осколка 0 = Н - ʋ0 t1 - 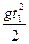 для второго осколка 0 = Н + ʋ0 t2 -
для второго осколка 0 = Н + ʋ0 t2 -  ;
большее время затратит на падение осколок, летящий t2;
искомое время Δt=t2 - t1 ;
проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу;
представлен правильный ответ с указанием единиц измерения искомой величины Δt = 4 с. ;
большее время затратит на падение осколок, летящий t2;
искомое время Δt=t2 - t1 ;
проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу;
представлен правильный ответ с указанием единиц измерения искомой величины Δt = 4 с.
|
Задача 2.
Ведро, в котором находится m = 10 кг смеси воды со льдом, внесли в комнату и сразу начали измерять температуру смеси. График зависимости температуры от времени t(t) изображен на рисунке. Какая масса льда была в ведре, когда внесли в комнату? Удельная теплоемкость воды с=4200 Дж/(кг оС), удельная теплота плавления льда l = 330 кДж/кг. Теплоемкостью ведра пренебречь.
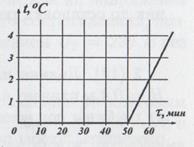
(10 баллов)
| Возможное решение | |
Таяние льда в ведре и нагревание воды происходит за счет теплообмена с окружающей средой. Так как рост температуры от времени в рассматриваемом диапазоне является линейным, то мощность Р теплового потока можно считать постоянной. Уравнение теплового баланса для таяния льда mлl = Рt0, где mл – масса льда в ведре, t0 = 50 мин – время таяния льда. Уравнение теплового баланса при нагревании воды mсΔt = РΔt, где Δt - время нагревания воды. Из графика определим 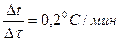 . Таким образом . Таким образом 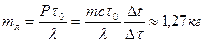
| |
| Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы:
описаны все вновь вводимые в решении буквенные обозначения физических величин;
представлено полное верное объяснение с указанием наблюдаемых явлений и законов:
пояснили, что таяние льда в ведре и нагревание воды происходит за счет теплообмена с окружающей;
Заметили, что рост температуры от времени в рассматриваемом диапазоне является линейным, следовательно мощность Р теплового потока можно считать постоянной
средой записано уравнение теплового баланса для таяния льда mлl = Рt0;
уравнение теплового баланса при нагревании воды mсΔt = РΔt;
определим 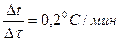 проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу;
представлен правильный ответ с указанием единиц измерения искомой величины
проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу;
представлен правильный ответ с указанием единиц измерения искомой величины 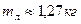
|
Задача 3.
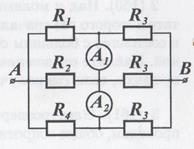
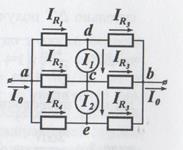
Резисторы сопротивлениями R1 = 1 кОм, R2 = 2 кОм, R3 = 3 кОм, R4 = 4 кОм подключены к источнику постоянного напряжения U0 = 33В через клеммы А и В. К резисторам подключили два идеальных амперметра А1, А2. Определите показания амперметров I1, I2.
Баллов).
| Возможное решение | |||
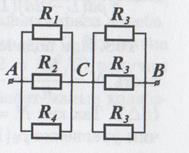
Определим токи Ii, текущие через резисторы Ri (i = 1, 2, 3, 4). Так как амперметры идеальные, то можно рассмотреть эквивалентную электрическую цепь. Для этой цепи 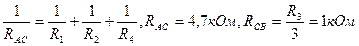 , RAB = RAC + RCB = , RAB = RAC + RCB = 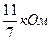 . Полный ток в цепи . Полный ток в цепи 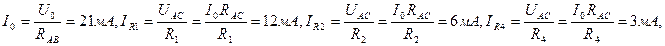  Для определения показания амперметров запишем закон сохранения токов в узлах d и с (выбранное направление токов указано на рисунке): I1 = IR1 – IR3 = 5 мА, I2 = IR3 – IR4 = 4 мА Для определения показания амперметров запишем закон сохранения токов в узлах d и с (выбранное направление токов указано на рисунке): I1 = IR1 – IR3 = 5 мА, I2 = IR3 – IR4 = 4 мА
| |||
| Критерии оценивания выполнения задания | Баллы | ||
| Приведено полное правильное решение, включающее следующие элементы: Сделан пояснительный рисунок; проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу определили сопротивление RAC; определили сопротивление RCB; определили сопротивление RAB; | |||
| определили I0; определили IR1; определили IR2; определили IR3; представлен правильный ответ с указанием единиц измерения искомой величины: I1 = 5 мА, I2 = 4 мА | |||
Задача 4.
Кусок льда привязан нитью ко дну цилиндрического сосуда с водой (см. рис.). Над поверхностью воды находится некоторый объём льда. Нить натянута с силой Т= 1Н. На сколько и как изменится уровень воды в сосуде, если лёд растает? Площадь дна сосуда S= 400 см2, плотность воды ρ= 1 г/см3.
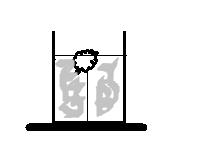
(10 баллов)
| Возможное решение | |
Запишем условие плавания куска льда в воде: mлg+ Т =FА= ρ вVп.ч.g; где Vп.ч – объём погружённой в воду части куска льда. Найдём первоначальный уровень воды в сосуде 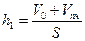 (1), где V о – первоначальный объём воды в сосуде до таяния льда. Соответственно (1), где V о – первоначальный объём воды в сосуде до таяния льда. Соответственно 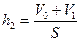 (2), где h2 – уровень воды в сосуде, после таяния льда, V 1 – объём воды, полученной из льда. Решая совместно (1) и (2), получаем h 1 –h 2 = (V п.ч. –V1 )/S; найдём Vп.ч = (m лg+Т)/(ρ в.g). Учтём mл = m1, где m1 - масса воды, полученной изо льда m1 = ρвV1; V1 = mл/ρв. Тогда h 1 –h 2 = ((mлg+Т)/ ρ вg. – m л / ρ в )/ S = 2,5 мм (2), где h2 – уровень воды в сосуде, после таяния льда, V 1 – объём воды, полученной из льда. Решая совместно (1) и (2), получаем h 1 –h 2 = (V п.ч. –V1 )/S; найдём Vп.ч = (m лg+Т)/(ρ в.g). Учтём mл = m1, где m1 - масса воды, полученной изо льда m1 = ρвV1; V1 = mл/ρв. Тогда h 1 –h 2 = ((mлg+Т)/ ρ вg. – m л / ρ в )/ S = 2,5 мм
| |
| Критерии оценивания выполнения задания | Баллы |
| Приведено полное правильное решение, включающее следующие элементы: cделан пояснительный рисунок, с указанием всех действующих сил; описаны все вновь вводимые в решении буквенные обозначения физических величин; представлено полное верное объяснение с указанием наблюдаемых явлений и законов: записано условие плавания куска льда в воде: mлg + Т = FА= ρвVп.ч.g; записали формулу для расчета h1; записали формулу для расчета h2; проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу: h 1 –h 2 = (V п.ч. –V1 )/S; Vп.ч = (mлg+Т)/(ρв.g); V1 = mл/ρв; h 1 –h 2 = ((mлg+Т)/ ρ вg. – m л / ρ в )/ S. Представлен правильный ответ с указанием единиц измерения искомой величины: h 1 –h 2 = 2,5 мм |
Задача 5.
Чему должен быть равен минимальный коэффициент трения μ между шинами и поверхностью наклонной дороги с уклоном α=30о, чтобы автомобиль мог двигаться по ней вверх с ускорением a=0,6 м/с2?
(10 баллов)
| Возможное решение | |
Cилой, вынуждающей двигаться автомобиль является сила трения покоя F(тр.п)макс. Проскальзыванием колёс и силой трения качения пренебрегаем.
Укажем все действующие на автомобиль силы и запишем 2 закон Ньютона
ma = Fтр.п. + mg. Через проекцию на ось ОХ: Fтр.п. – mg  = ma
Fтр.п.=μN; OY: N = mg = ma
Fтр.п.=μN; OY: N = mg 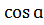 Þ Fтр.п.=μ mg Þ Fтр.п.=μ mg 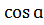 Þ μmg Þ μmg 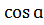 – mg – mg  = ma; μ = (а + g = ma; μ = (а + g  )/g )/g 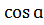 ; μ = 0,64. ; μ = 0,64.
| |
| Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы:
cделан пояснительный рисунок, с указанием всех действующих сил;
представлено полное верное объяснение с указанием наблюдаемых явлений и законов (II закон Ньютона);
cилой, вынуждающей двигаться автомобиль является сила трения покоя F(тр.п)макс;
Проскальзыванием колёс и силой трения качения пренебрегаем;
проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу:
ОХ: Fтр.п. – mg  = ma
OY: N = mg = ma
OY: N = mg 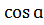 μmg
μmg 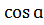 – mg – mg  = ma
μ = (а + g = ma
μ = (а + g  )/g )/g 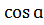 Представлен правильный ответ с указанием единиц измерения искомой величины: μ = 0,64
Представлен правильный ответ с указанием единиц измерения искомой величины: μ = 0,64
|






