Решения
Задача 1.
Два путника идут из пункта А в пункт В. Первый путник первую треть дистанции идет со скоростью 2 v 0, а оставшийся путь со скоростью v 0. Второй путник первую треть времени идет со скоростью 2 v 0, а оставшийся путь со скоростью v 0. Какой путник придет быстрее и во сколько раз меньше времени он затратит на весь путь?
(10 баллов)
| Возможное решение | |
Пусть S – расстояние между пунктами А и В, t1 (t2)– полное время движения первого (второго) путника. Первый путник пройдет расстояние S за время t1 =  . Для второго путника: S = . Для второго путника: S = 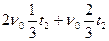 или или  Таким образом второй путник придет быстрее и затратит времени в Таким образом второй путник придет быстрее и затратит времени в  раз меньше. раз меньше.
| |
| Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы:
описаны все вновь вводимые в решении буквенные обозначения физических величин (расстояние между пунктами, время движения первого и второго путника);
правильно записаны формулы, выражающие закономерности, применение которых необходимо для решения задачи выбранным способом:
t1 =  .
S = .
S = 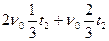 Проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу:
для первого путника t1
Проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу:
для первого путника t1  для второго путника
для второго путника  представлен правильный ответ
представлен правильный ответ
 раз меньше. раз меньше.
|
Задача 2.
В сосуде находится 1 кг смеси воды и льда. Для нагревания смеси до температуры t1 = +100С необходимо теплоты в 2 раза больше, чем выделяется теплоты при охлаждении смеси до температуры t2 = -50С. Определите первоначальные массы льда и воды в сосуде, если удельная теплоёмкость воды c в = 4,2 кДж/(кг∙°C), льда c л = 2,1 кДж/(кг∙°C), удельная теплота плавления льда λ = 340 кДж/кг. Теплоемкостью сосуда пренебречь.
(10 баллов)
| Возможное решение | |
Пусть mл – масса льда, mв – масса воды. Смесь воды и льда в сосуде находится при температуре t0 = 00С. Для нагревания смеси до температуры t1 = +100С необходимо количество теплоты Q1 = mлl + (mл + mв)св(t1 - t0). При охлаждении смеси до температуры t1 = -50С выделяется количество теплоты Q2 = mлl - (mл + mв)св(t2 - t0). Из условия
Q1 = 2Q2 найдем отношение  Так как mл + mв = 1 кг, то mл = 647 г, mв = 353 г. Так как mл + mв = 1 кг, то mл = 647 г, mв = 353 г.
| |
| Критерии оценивания выполнения задания | Баллы |
| Приведено полное правильное решение, включающее следующие элементы: описаны все вновь вводимые в решении буквенные обозначения физических величин (масса воды, масса льда); представлено полное верное объяснение с указанием наблюдаемых явлений и законов: обоснован выбор температуры смеси (воды и льда); для нагревания смеси Q1 = mлl + (mл + mв)св(t1 - t0) для охлаждения смеси Q2 = mлl - (mл + mв)св(t2 - t0); проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу; представлен правильный ответ с указанием единиц измерения искомой величины mл = 647 г mв = 353 г. |
Задача 3.
В сообщающихся сосудах с вертикальными стенками и площадью сечения S = 20 см2 находится вода. В один из сосудов наливают масло массой m = 160 г, при этом вода остается в обоих сосудах и не перемешивается с маслом. Определите разность Dh уровней жидкостей в сосудах. Плотность масла ρм = 800 кг/м3, плотность воды ρв = 1000 кг/м3.
(10 баллов)
| Возможное решение | |
Пусть hм – высота столба масла, hв – высота столба воды в другом сосуде, находящейся выше общего уровня воды в обоих сосудах. Так как давление этих столбов жидкостей должно быть одинаковыми ρмghм = ρвghв, то hв  . Из уравнения m = ρмhмS найдем высоту столба масла . Из уравнения m = ρмhмS найдем высоту столба масла  . Разность уровней жидкостей в сосудах Dh = hм - hв = hм (1 - . Разность уровней жидкостей в сосудах Dh = hм - hв = hм (1 -  ) = ) = 
| |
| Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы:
описаны все вновь вводимые в решении буквенные обозначения физических величин (высота столба масла, высота столба воды в другом сосуде);
правильно записаны формулы, выражающие закономерности, применение которых необходимо для решения задачи выбранным способом:
равенство давлений столбов жидкости ρмghм = ρвghв
высота столба масла  Проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу:
hв =
Проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу:
hв =  представлен правильный ответ с указанием единиц измерения искомой величины hв = 2 см.
представлен правильный ответ с указанием единиц измерения искомой величины hв = 2 см.
|
Задача 4.
Схема, состоящая из амперметра А, трех одинаковых резисторов сопротивлением R = 10 Ом и ключа К, подсоединена к источнику постоянного напряжения U. Чему равно сопротивление амперметра, если его показание изменилось на 25% после замыкания ключа.
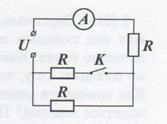
(10 баллов)
| Возможное решение | |
До замыкания ключа ток через амперметр I1 =  После замыкания ключа ток через амперметр I2 = После замыкания ключа ток через амперметр I2 =  Так как полное сопротивление цепи уменьшилось, то показание амперметра увеличилось. При изменении показаний на 25%, имеем I2 = nI1, n = 1,25. Используя соотношение между токами I2 и I1, найдем сопротивление амперметра Так как полное сопротивление цепи уменьшилось, то показание амперметра увеличилось. При изменении показаний на 25%, имеем I2 = nI1, n = 1,25. Используя соотношение между токами I2 и I1, найдем сопротивление амперметра  Ом. Ом.
| |
| Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы:
описаны все вновь вводимые в решении буквенные обозначения физических величин;
представлено полное верное объяснение с указанием наблюдаемых явлений и законов (закон Ома для участка цепи, расчет общего сопротивления цепи ):
До замыкания ключа ток через амперметр I1 =  ;
После замыкания ключа ток через амперметр I2 = ;
После замыкания ключа ток через амперметр I2 =  ;
проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу;
представлен правильный ответ с указанием единиц измерения искомой величины RA = 5 Oм ;
проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу;
представлен правильный ответ с указанием единиц измерения искомой величины RA = 5 Oм
|
Задача 5.
Машина, двигаясь со скоростью v 0 = 72 км/ч, начинает тормозить и останавливается через t0 = 10 с. Считая ускорение машины постоянным, определите тормозной путь S машины и среднюю скорость v ср машины за первую половину времени торможения.
(10 баллов)
| Возможное решение | |
Пусть а – ускорение торможения машины. Так как машина останавливается за время t0, то из условия v к = v 0 - аt0 = 0, найдем ускорение а =  Тормозной путь машины S = Тормозной путь машины S =  = 100 м. За первую половину времени t1 = = 100 м. За первую половину времени t1 = 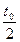 машина пройдет путь S1 = машина пройдет путь S1 =  . На этом участке средняя скорость машины равна . На этом участке средняя скорость машины равна 
| |
| Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы:
описаны все вновь вводимые в решении буквенные обозначения физических величин;
представлено полное верное объяснение с указанием наблюдаемых явлений и законов:
записано уравнение скорости для равноускоренного движения в общем виде;
выразили ускорение;
записали формулу для расчета тормозного пути;
проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу;
записали формулу для расчета пройденного пути за первую половину времени;
представлен правильный ответ с указанием единиц измерения искомой величины
S = 100 м

|






