Всероссийская олимпиада школьников по физике (2016-2017 уч.г.) Школьный этап, 7 класс
Решения
Задача 1.
Оптический микроскоп позволяет различить объекты размером около 0,0000003 м. Можно ли в такой микроскоп увидеть капельку воды, по диаметру которой укладывается сто, тысяча, миллион молекул? Поясните ответ. Диаметр молекулы воды равен примерно 0,0000003 мм. Можно ли в такой микроскоп увидеть молекулу воды?
(10 баллов)
| Возможное решениеи критерии оценивания выполнения задания | Баллы |
| Приведено полное правильное решение, включающее следующие элементы: проведены необходимые преобразования и расчёты, приводящие к правильному числовому ответу, и представлен ответ в одной системе измерения: 0,0000003 мм ·100 = 0,00000003 м 0,0000003 мм ·1000 = 0,0000003 м 0,0000003 мм ·1000000 = 0,0003 м Приведено полное правильное объяснение на первый вопрос: в оптический микроскоп можно увидеть только такую капельку воды, диаметр которой не менее чем в 1000 раз больше диаметра молекулы воды. Дан правильный ответ на второй вопрос: молекулы воды нельзя увидеть в оптический микроскоп. 0,0000003 мм < 0,0000003 м |
Задача 2.
Пассажир, сидящий у окна в поезде А, идущего со скоростью v 1 = 72 км/ч, видит встречный поезд Б в течение некоторого времени. Если бы оба поезда двигались в одном направлении при неизменных скоростях, то время наблюдения пассажиром поезд Б увеличилось бы втрое. Определите скорость v 2 поезда Б.
(15 баллов)
| Возможное решение | |
Пусть длина поезда L. При встречном движении поездов пассажир видит поезд Б в течение времени 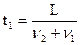 , а при движении поездов в одном направлении – за , а при движении поездов в одном направлении – за 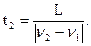 Так как t2 = 3t1, то 3| v 2 - v 1| = v 2 + v 1. При v 2 > v 1 имеем 3(v 2 - v 1) = v 2 + v 1 или v 2 = 2 v 1 = 144 км/ч. При v 2< v 1 имеем 3(v 1 - v 2) = v 2 + v 1 или v 2 = 20 v 1/2 = 36 км/ч. Так как t2 = 3t1, то 3| v 2 - v 1| = v 2 + v 1. При v 2 > v 1 имеем 3(v 2 - v 1) = v 2 + v 1 или v 2 = 2 v 1 = 144 км/ч. При v 2< v 1 имеем 3(v 1 - v 2) = v 2 + v 1 или v 2 = 20 v 1/2 = 36 км/ч.
| |
| Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы:
описаны все вновь вводимые в решении буквенные обозначения физических величин (длина поезда, время наблюдения поезда Б при встречном движении, время наблюдения поезда Б при движении поездов в одном направлении);
правильно записаны формулы, выражающие закономерности, применение которых необходимо для решения задачи выбранным способом:
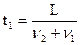
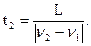 3| v 2 - v 1| = v 2 + v 1;
проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (для случая v 2 > v 1 и v 2< v 1);
в общем виде приведена конечная формула (v 2 = 2 v 1, v 2 = 20 v 1/2)
представлен правильный ответ с указанием единиц измерения искомой величины (v 2 = 144 км/ч, v 2 = 36 км/ч).
3| v 2 - v 1| = v 2 + v 1;
проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (для случая v 2 > v 1 и v 2< v 1);
в общем виде приведена конечная формула (v 2 = 2 v 1, v 2 = 20 v 1/2)
представлен правильный ответ с указанием единиц измерения искомой величины (v 2 = 144 км/ч, v 2 = 36 км/ч).
|
Задача 3.
Вам даны кастрюля, ведро с водой и чайник, в который необходимо как можно точнее налить воду объемом 2,5 л. Как это можно сделать? (Вместимость ведра - 8 л, кастрюли 5 л, чайника – 3 л) Сделайте пояснительный рисунок.
(5 баллов)
| Возможное решение | |
| Надо заполнить кастрюлю водой, затем медленно наклонять ее до тех пор, пока она не примет положение, показанное на рисунке. Очевидно, в кастрюле останется вода объемом, равным половине объема кастрюли, т.е. 2,5 л | |
| Критерии оценивания выполнения задания | Баллы |
Приведено полное верное объяснение, включающее следующие элементы:
Идея использования только кастрюли;
выполнен верный рисунок;
Даны пояснения к рисунку.
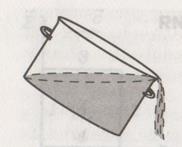
|
Задача 4.
Два друга, Петр и Павел, поехали на поезде. У Петра был билет в первый вагон, а у Павла - в последний (вагоны нумеруются от локомотива). На одной из промежуточных остановок локомотив перецепили к хвосту поезда, так, что Петр приехал в конечный пункт в последнем вагоне, а Павел - в первом. Сравните пути вагонов, в которых ехали Петр и Павел. Ответ поясните.
(5 баллов)
| Возможное решение | |
| В процессе перецепления локомотива расстояние между любыми двумя вагонами, очевидно, не менялось, так как вагоны не расцеплялись. Таким образом, независимо от способа перецепления локомотива, в процессе перецепления вагоны прошли одинаковое расстояние. Также можно заметить, что и до промежуточной остановки, и после нее вагоны также проходили одинаковый путь. Итого, пути вагонов, в которых ехали Петр и Павел, одинаковы. | |
| Критерии оценивания выполнения задания | Баллы |
| Приведено полное верное объяснение, включающее следующие элементы: Указано, что: вагоны не расцеплялись; в процессе перецепления локомотива расстояние между любыми двумя вагонами не менялось; в процессе перецепления вагоны прошли одинаковое расстояние; до промежуточной остановки, и после нее вагоны также проходили одинаковый путь; представлен правильный ответ: пути вагонов, в которых ехали Петр и Павел, одинаковы. |
Всероссийская олимпиада школьников по физике (2016-2017 уч.г.) Школьный этап, 8 класс
Решения
Задача 1.
Сколько нужно смешать горячей воды, имеющей температуру 800С, и холодной, имеющей температуру 200С, чтобы получить 60 л воды с температурой 400С? Плотность воды 1000 кг/м3.
(10 баллов)
| Возможное решение | |
Пусть mг – масса горячей воды, тогда масса холодной воды mх = m – mг = rV - mг. В результате теплообмена горячая вода отдает количество теплоты Qг = сmг(tг – t), а холодная вода получает количество теплоты Qх = сmх(t – tх), где t – температура смеси и tг(tх) – температура горячей (холодной) воды. Согласно уравнению теплового баланса Qг = Qх. Из уравнения сmг(tг – t) = с(rV - mг)(t – tх) находим mг = 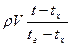 ; mг = 20 кг, mх = 40 кг. ; mг = 20 кг, mх = 40 кг.
| |
| Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы:
описаны все вновь вводимые в решении буквенные обозначения физических величин (масса горячей (холодной) воды, температура воды)
правильно записаны формулы, выражающие закономерности, применение которых необходимо для решения задачи выбранным способом:
mх = m – mг = rV - mг
Qг = сmг(tг – t) - количество теплоты отдает горячая вода
Qх = сmх(t – tх) - количество теплоты получает холодная вода
сmг(tг – t) = с(rV - mг)(t – tх)
проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу;
mг = 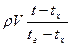 представлен правильный ответ с указанием единиц измерения искомой величины
mг = 20 кг
mг = 40 кг
представлен правильный ответ с указанием единиц измерения искомой величины
mг = 20 кг
mг = 40 кг
|
Задача 2.
Два поезда одновременно выехали из пунктов А и В навстречу друг другу. Первый поезд прибыл в пункт В через t1 = 4 часа после встречи поездов, а второй в пункт А через t2 = 9 часов после встречи. Определите, сколько часов был в пути первый поезд.
(10 баллов)
| Возможное решение | |
Пусть v 1 ( v 2) -скорость первого (второго) поезда, t – время встречи поездов. Из условия задачи v 1t = v 2t2, v 2t = v 1t1 получим  или или  . Таким образом, первый поезд был в пути T = t + t1 = . Таким образом, первый поезд был в пути T = t + t1 =  = 10 часов. = 10 часов.
| |
| Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы:
описаны все вновь вводимые в решении буквенные обозначения физических величин (скорость первого (второго) поезда, время встречи поездов; общее время в пути первого поезда)
правильно записаны формулы, выражающие закономерности, применение которых необходимо для решения задачи выбранным способом:
v 1t = v 2t2
v 2t = v 1t1
проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу;
 T =
T =  представлен правильный ответ с указанием единиц измерения искомой величины ( T = 10 часов).
представлен правильный ответ с указанием единиц измерения искомой величины ( T = 10 часов).
|
Задача 3.
На легком жестком двухъярусном рычаге, сложной конструкции, уравновешены 4 груза. Длины частей рычага заданы на рисунке. Найдите массу неизвестного груза (mx), если массы трех остальных грузов известны (m = 6 кг)?
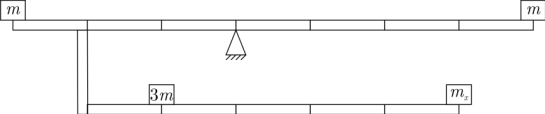
(10 баллов)
| Возможное решение | |
| Несмотря на сложную конструкцию нижней «полки» рычага, для системы (рычаг + грузы) можно воспользоваться правилом моментов сил. Вычислим моменты сил относительно точки подвеса. 𝑚𝑔3𝐿+3𝑚𝑔𝐿=𝑚4𝐿+𝑚𝑥𝑔3𝐿. Откуда 𝑚𝑥=2m/3=4 кг. | |
| Критерии оценивания выполнения задания | Баллы |
| Приведено полное правильное решение, включающее следующие элементы: выполнен рисунок с указанием всех действующих сил; указано плечо каждой силы; правильно записаны формулы, выражающие закономерности, применение которых необходимо для решения задачи выбранным способом: правило моментов сил: 𝑚𝑔3𝐿+3𝑚𝑔𝐿=𝑚𝑔4𝐿+𝑚𝑥𝑔3𝐿 Проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу: 𝑚𝑥=2m/3 представлен правильный ответ с указанием единиц измерения искомой величины: 𝑚𝑥=4 кг. |
Задача 4.
Кусок пористого льда (содержащего воздушные пузырьки) плавает в воде, погрузившись на 1/2 своего объема. Какую часть объема всего куска льда занимают воздушные пузырьки, если отношение плотностей льда и воды равно 0,9?
(10 баллов)
| Возможное решение | |
Обозначим ρл – плотность чистого льда (без воздушных пузырьков), ρв – плотность воды, Vп – объем воздушных пузырьков, Vл – объем чистого льда, V – объем всего куска льда (с воздушными пузырьками). Vл = V – Vп. Из условия плавания льда (закон Архимеда): mg = FАрх, mg = ρлVлg = ρл(V – Vп)g, FАрх =  ρвVg получим ρл(V – Vп)g = ρвVg получим ρл(V – Vп)g =  ρвVg Þ ρвVg Þ  . Так как . Так как 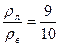 , то , то 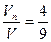 . .
| |
| Критерии оценивания выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы:
описаны все вновь вводимые в решении буквенные обозначения физических величин (плотность чистого льда, плотность воды, объем воздушных пузырьков, объем чистого льда, объем всего куска льда);
правильно записаны формулы, выражающие закономерности, применение которых необходимо для решения задачи выбранным способом:
Vл = V – Vп.
Условие плавания льда: mg = FАрх.
mg = ρл(V – Vп)g
FАрх =  ρвVg
ρл(V – Vп)g = ρвVg
ρл(V – Vп)g =  ρвVg
Проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу: ρвVg
Проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу:
 представлен правильный ответ
представлен правильный ответ 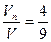
|






