Взаимодействие движущихся зарядов. Сила Лоренца
Движущийся заряд создает в окружающем его пространстве помимо электрического еще и магнитное поле, существование которого обусловлено релятивистскими свой-ствами пространства и времени. Силовой характеристикой магнитного поля является вектор магнитной индукции 
. В результате обобщения экспериментальных данных был получен закон, определяющий индукцию 
поля точечного заряда, движущегося с постоянной нерелятивистской скоростью
, (1.1)
где 
- радиус-вектор, проведенный от заряда к точке наблюдения, 
- магнитная постоянная.
Вектор 
перпендикулярен плоскости, в которой расположены векторы 
и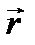 
, образуя тройку векторов правой ориентации (рис.1.1). Величина 
обратно пропор–циональна 
, максимальна в направлении перпендикулярном скорости заряда, и равна нулю в направлении, совпадающим с направлением движения заряда. Линии индукции магнитного поля 
являются замкнутыми окружностями, “нанизанными” на ось, определяемую вектором 
(рис.1.2).
| Рис.1.1 |
| Рис.1.2 |
Силу взаимодействия двух движущихся электрических зарядов можно разделить на две составляющие – электри- ческую и магнитную.
Электрическая составляющая не зависит от движения зарядов и описывается законом Кулона
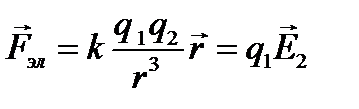, (1.2)
где 
- вектор напряженности электрического поля, создавае- мого вторым зарядом. Магнитная составляющая, зависящая от скорости электрического заряда, имеет следующий вид
, (1.3)
где 
- магнитная индукция, обусловленная зарядом 
.
Следовательно, полная сила взаимодействия между движущимися зарядами определяется выражением
. (1.4)
Обобщая эту формулу, можно считать, что на электрический заряд, движущийся в электрическом 
и магнитном 
полях, действует сила
. (1.5)
Эту силу называют силой Лоренца.
Выражение для магнитной составляющей силы Лоренца может быть использовано для установления физического смысла и единицы измерения магнитной индукции. Из формулы
следует, что индукция B численно равна силе, которая действует на единичный положительный заряд, движущийся перпендикулярно вектору 
со скоростью, равной единице:
, 
.
Единица измерения магнитной индукции называется Тесла (Тл).
1.2. Закон Био – Савара - Лапласа и его применение
к расчёту магнитного поля прямого и кругового токов
Используя выражение (1.1) для индукции поля движу- щегося заряда, выведем формулу для индукции поля элемента тока.
Пусть магнитное поле создается произвольным тонким проводником, по которому течет ток 
(рис.1.3). Выделим элемент проводника dl. Число носителей тока в данном элементе равно
, (1.6)
где n – концентрация носителей, а S – площадь сечения проводника.
| Рис.1.3 |
| Рис.1.4 |
| r |
| Рис.1.3 Рис.1.4 |
|
Каждый носитель тока создает магнитное поле, индук- ция которого в некоторой точке А определяется выражением
, (1.7)
где 
- средняя скорость упорядоченного движения носи- телей тока, 
- вектор, соединяющий 
с точкой А.
Поле, создаваемое элементом тока dl, будет равно
. (1.8)
Приняв во внимание, что
,
получим закон Био - Савара – Лапласа
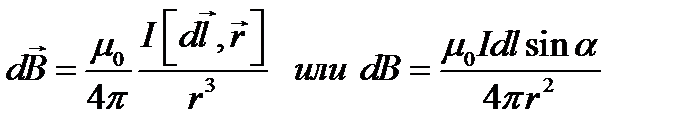, (1.9)
где 
- угол между векторами 
и 
.
Вектор 
перпендикулярен плоскости, проходящей через dl и точку A, а его направление определяется правилом правого винта.
Результирующее поле, созданное проводником с током 
, в соответствии с принципом суперпозиции находится путем интегрирования по всем элементам тока.
Воспользуемся формулой (1.9) для расчета индукции магнитного поля прямого и кругового токов. Пусть поле в некоторой точке А создается током 
, текущим по тонкому прямому проводнику длиной l (рис.1.4). Все 
в данной точке имеют одинаковое направление (за чертеж), поэтому сложение векторов можно заменить сложением модулей
. (1.10)
Учитывая, что 
, приведем (1.10) к виду, удобному для интегрирования
.
Интегрируя в пределах от 
до 
, получим
. (1.11)
В частности, для прямого тока бесконечной длины (
), получим
. (1.12)
Вычислим теперь магнитное поле на оси кругового тока. Вектор 
, создаваемый элементом тока 
в произ- вольной точке А, лежащей на оси OX, показан на рис.1.5. Векторы 
от всех элементов контура будут образовывать симметричный конический веер, поэтому результирующий вектор 
направлен вдоль оси OX.
| Рис.1.5 |
Так как 
(1.13)
Тогда
. (1.14)
Если учесть, что 
, то получим окончательно выражение для индукции магнитного поля B на оси кругового тока
. (1.15)
В центре витка (x =0)
, (1.16)
а для 
. (1.17)
Введя понятие магнитного момента контура с током
, (1.18)
где S – площадь контура, 
- положительная нормаль к контуру, направление которой связано с направлением тока правилом правого винта, выражение (1.17) приводится к виду
. (1.19)
Эта формула подобна формуле для напряженности поля электрического диполя на его оси, что дает основание контурный ток называть магнитным диполем. Таким образом, контур с током в магнетизме играет ту же роль, что и электрический диполь в электростатике, а дипольный магнитный момент 
является аналогом электрического момента 
.
