В данной таблице приведены производные основных элементарных функций и правила дифференцирования, которые нужно очень хорошо выучить, чтобы применять к решению примеров:

Например:
Найдите производную данной функции:
1) 
2) 
3) 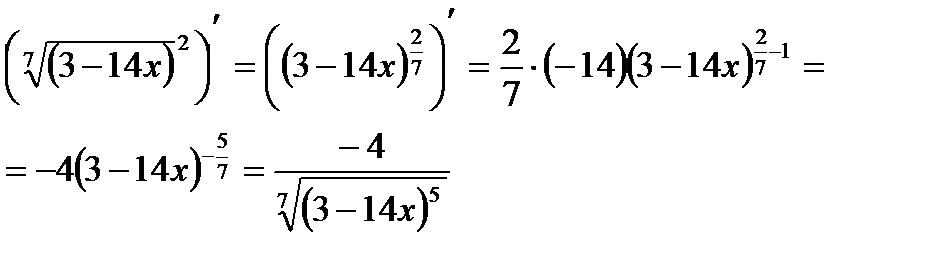
4) 
5) 
6) 
7) 
8) 
Элементы исследования функции с помощью производной
Производные применяют для исследования графиков функций:
устанавливают промежутки монотонности; точки экстремума; наибольшее и наименьшее значения функции на отрезке.
Функцией называется правило f, по которому каждому элементу х множества Х ставится в соответствие единственный элемент у множества У.
План исследования функций:
1. Область определения
2. Множество значений
3. Четность, не четность
4. Непрерывность
5. Нули функции
6. Промежутки знакопостоянства
7. Промежутки монотонности
8. Критические точки
9. Точки экстремума
10. Экстремум функции
11. Наибольшее и наименьшее значение функции
Чтобы исследовать функцию полезно найти её производную и приравнять её к нулю. Тем самым найдём стационарные точки. Затем исследуем промежутки в окрестности стационарных точек:
если производная положительна, то функция возрастает;
если производная отрицательна, то функция убывает.
Стационарные точки становятся точками экстремума, если производная меняет знак: с «+» на «-» точка max; с «-» на «+» точка min

Например:

Используя эту подготовительную работу можно строить график.
Необходимо ещё найти значение функции в стационарных точках, и добавить дополнительные точки для более точного построения.
ПРИМЕР 1




ПРИМЕР 2




ПРИМЕР 3
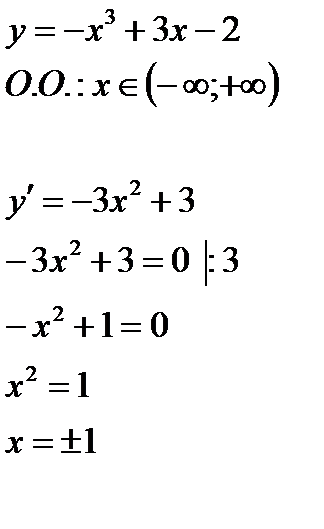



ПРИМЕР 4




Контрольные вопросы и задания для самостоятельного решения по разделу 8
Ответьте на вопросы:
1) Как найти производную степенной функции?
2) Как найти стационарные точки?
3) Что такое точки экстремума?
4) Как найти промежутки монотонности функции?
Решите упражнения:
№ 1 Найти производную функции: № 2 Постройте график функции:
1)  1)
1) 
2)  2)
2) 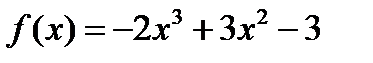
3)  3)
3) 
4)  4)
4) 
5)  5)
5) 
6)  6)
6) 
Проверьте своё решение:
Ответы:
№ 1
1) 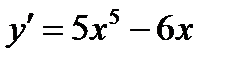 2)
2) 
3) 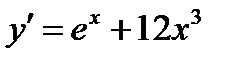 4)
4) 
5)  6)
6) 
№ 2
1) 
2) 
3) 
4) 
5) 
6) 
Площадь криволинейной трапеции
Что такое «криволинейная трапеция»?
Фигура, ограниченная функцией  прямыми х = а, х = b и осью Ох называется криволинейной трапецией.
прямыми х = а, х = b и осью Ох называется криволинейной трапецией.
Вычисляется площадь по формуле Ньютона-Лейбница:

Число a называется нижним пределом интегрирования, а число b ¾ верхним пределом интегрирования.
Криволинейная трапеция может быть различного вида:
I.Стандартная криволинейная трапеция:
(нижнее основание – ось Ох, верхнее основание функция f(x)).


II. Трапеция, расположенная «вверх ногами»:
(верхнее основание – ось Ох, нижнее основание функция f(x)).






