Основные понятия:

Одним из важнейших умений в математике – это умение решать квадратные уравнения.


Алгоритм решения квадратного уравнения по формуле корней:
1) Найти число, называемое дискриминантом квадратного уравнения
и равное D = b²- 4ac.
2) Дискриминант показывает сколько корней имеет уравнение
I. если D<0, то данное квадратное уравнение не имеет корней;
II. 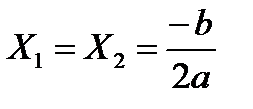 если D=0, то данное квадратное уравнение имеет единственный корень, который равен
если D=0, то данное квадратное уравнение имеет единственный корень, который равен
III. если D>0, то данное квадратное уравнение имеет два корня, которые равны

Например:

Умение удачно ввести новую переменную – облегчает решение:

Дробно-рациональные уравнения
Как ясно из названия, в этих уравнениях обязательно присутствуют дроби. Но не просто дроби, а дроби, у которых есть неизвестное в знаменателе.
ОДЗ – (Область Допустимых Значений).
Это те значения икса, которые могут быть в принципе. Т.к. делить на ноль нельзя, знаменатели в дробно-рациональных уравнениях не должны равняться нулю. Перед решением внимательно исследуйте пример и определите ОДЗ. Все найденные в процессе решения корни нужно проверять: не обратят ли они какой-либо из знаменателей в ноль (такой корень будет посторонним и в окончательный ответ не попадёт).

Контрольные вопросы и задания для самостоятельного решения по разделу 4
Ответьте на вопросы:
1) Какое уравнение называется квадратным?
2) Что такое дискриминант?
3) Как решать биквадратное уравнение?
4) Какое уравнение называется дробно-рациональным?
5) Что такое ОДЗ?
Решите упражнения:
№ 1
1) 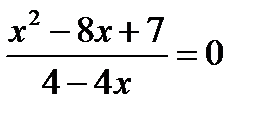 2)
2) 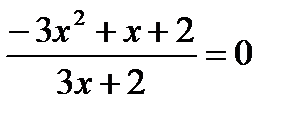
3)  4)
4) 
5)  6)
6) 
№ 2
1)  2)
2) 
3)  4)
4) 
5)  6)
6) 
№ 3
1)  2)
2) 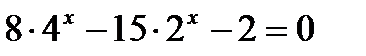
3)  4)
4) 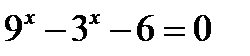
5)  6)
6) 
7)  8)
8) 
Проверьте своё решение:
№ 1
1) 7 2) 1 3) 3
4) - 2 5) 4 6) - 2
№ 2
1) 2 2) 1; 0 3) 1
4) 2; 1 5) 1 6) 1
№3
1) 2 2) 1 3) - 2; 5 4) 1
5) - 1; 3 6) - 5 7) 2 8) - 1; 6
Логарифмы.
I Логарифмические уравнения
Что такое логарифмическое уравнение?
Это уравнение, в котором неизвестные (иксы) и выражения с ними находятся внутри логарифмов.
Например:
log2х = 32
log3х = log39
log3(х2-3) = log3(2х)
logх+1(х2+3х-7) = 2
lg2(x+1)+10 = 11lg(x+1)
А что же такое логарифм?

Т.е. logab = c
(а - это основание, которое нужно возвести в степень с, чтобы получить b).

Любое число можно представить в форме логарифма:

т.е.

Чтобы решать уравнения, нужно знать свойства логарифмов:

Эти формулы верны безо всяких оговорок для положительных чисел. Но в уравнениях используются неизвестные, на которые накладывается ограничение:
подлогарифмическое выражение больше нуля, а основание логарифма и больше нуля и не равно единице!
logab = c
ОДЗ: b > 0, a > 0, a ≠ 1.!
В логарифмических уравнениях все найденные корни обязательно нужно проверять через ОДЗ!

Как решать логарифмические уравнения?
Процесс решения любого логарифмического уравнения заключается в переходе от уравнения с логарифмами к уравнению без них.
Например:
log3х = log39 ОДЗ: х > 0
х = 9
Ликвидировать логарифмы (потенцировать) безо всяких опасений можно, если у них:
а) одинаковые числовые основания
в) логарифмы слева и справа чистые (безо всяких коэффициентов) и находятся в гордом одиночестве.
Например: в уравнении log3х = 2log3(3х-1)
убирать логарифмы нельзя. Двойка справа не позволяет.
В примере log3х+log3(х+1) = log3(3+х)
тоже нельзя потенцировать уравнение. В левой части нет одинокого логарифма. Их там два.
Убирать логарифмы можно, если уравнение выглядит так и только так:
logа(.....) = logа(.....)
В скобках, где многоточие, могут быть какие угодно выражения. Простые, суперсложные, всякие. Какие угодно. Важно то, что после ликвидации логарифмов у нас остаётся более простое уравнение.
Примеры:
1) log7(2х-3) = log7х ОДЗ: 
2х-3 = х 2х – х = 3 х=3 (Ответ)
2) log7(50х-1) = 2 ОДЗ: 
log7(50х-1) = log772
50х-1 = 49 х = 1(Ответ)
3) 4)


5)


Ответ: 
II Логарифмические неравенства.






Контрольные вопросы и задания для самостоятельного решения по разделу 5
Ответьте на вопросы:
1) Что такое логарифм?
2) Что такое ОДЗ для логарифмической функции?
3) Назовите свойства логарифмов.
Решите упражнения:
№ 1. Решите уравнения:
1)  2)
2) 
3) 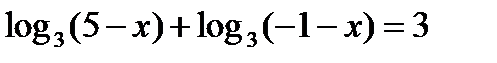 4)
4) 
5)  6)
6) 
№ 2.
Решите неравенства:
1)  2)
2) 
3)  4)
4) 
5)  6)
6) 










Проверьте своё решение:
Ответы:
№ 1.
1) 3 2) 4 3) - 4
4) 4 5) 3 6) 6
№ 2.
1)  2)
2) 
3)  4)
4) 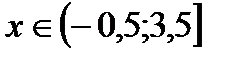
5)  6)
6) 
7)  8)
8) 
9)  10)
10) 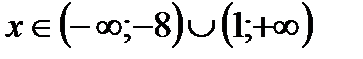
11)  12)
12) 
13) 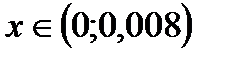 14)
14) 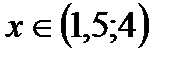
15)  16)
16) 




