Что такое тригонометрическое уравнение?
Тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрических функций.
Уравнения вида sin x = a; cos x = a; tg x = a; ctg x = a,
где x - переменная, а число  называются простейшими тригонометрическими уравнениями (для функций sin x и cos x |a| < 1)
называются простейшими тригонометрическими уравнениями (для функций sin x и cos x |a| < 1)
Есть несколько способов решать тригонометрические уравнения (с помощью единичной окружности или графически), но проще всего выучить формулы:
БЛОК I a > 0
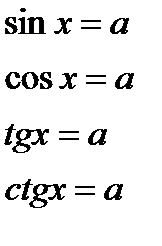 Þ
Þ 

БЛОК II – a < 0
 Þ
Þ 

БЛОК III частные случаи (а = 0, 1, – 1)
 Þ
Þ 

 Þ
Þ 

 Þ
Þ 

Примеры





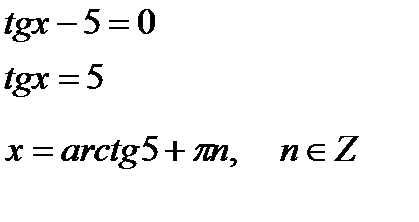
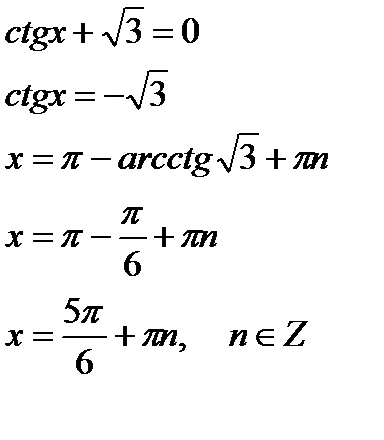
Ответ:  ;
; 
Однородные тригонометрические уравнения
Уравнение вида a sinx + b cosx = 0, где a ≠ 0, b ≠ 0
называется однородным тригонометрическим уравнением первой степени.

Уравнение вида a sin2x + b sinx cosx + c cos2x = 0,
где a ≠ 0, b ≠ 0, c ≠ 0
называется однородным тригонометрическим уравнением второй степени.
Например:

Пример:
a sin2x + b sinx cosx + c cos2x = 0
Выполним почленное деление на cos2x
(это возможно, т.к.: sinx и cosx не могут одновременно равняться нулю)

а tg2x + b tgx + c = 0
(уравнение, сводящееся к квадратному).
Итак, о днородные тригонометрические уравнения первой степени решаются делением обеих частей уравнения на cosx (или sinx). А уравнения второй степени решаются делением обеих частей на cos2x (или sin2x).
Пример 1. Решить уравнение:
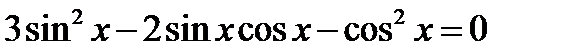
Решение:
Это уравнение является однородным относительно sinx и cosx.
Поэтому, разделив его на  , получим
, получим

Введем новую переменную  и решим квадратное уравнение
и решим квадратное уравнение



Ответ: 
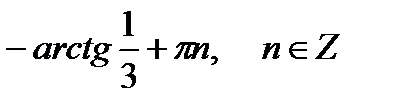
Пример 2.
3 sin2x – 4 sinx cosx + cos2x = 0
Т.к. cos2x ≠ 0, то

3tg2x – 4 tgx + 1 = 0 Замена: tgx = у.
3у2– 4 у + 1 = 0
D = 16 – 12 = 4
y1 = 1 или y2 = 1/3
tgx = 1 или tgx = 1/3
tgx = 1: Þ x = arctg (1/3) + πn, n ∈Z.
tgx = 1/3: Þ х = arctg1 + πn, x = π/4 + πn, n ∈Z.
Пример 3.
sin2x – 10 sinx cosx + 21cos2x = 0
Т.к. cos2x ≠ 0, то
tg2x – 10 tgx + 21 = 0 Замена: tgx = у.
у2 – 10 у + 21 = 0
у1 = 7 или у2 = 3
tgx = 7 или tgx = 3
tgx = 7: х = arctg7 + πn, n ∈Z
tgx = 3: х = arctg3 + πn, n ∈Z
Пример 4
sin22x – 6 sin2x cos2x + 5cos22x = 0
Т.к. cos22x ≠ 0,
то 3tg22x – 6tg2x +5 = 0
Замена: tg2x = у
3у2 – 6у + 5 = 0
D = 36 – 20 = 16
у1= 5 или у2 = 1
tg2x = 5 или tg2x = 1
tg2x = 5: 2х = arctg5 + πn, х = 1/2 arctg5 + π/2 n, n ∈Z
tg2x = 1: 2х = arctg1 + πn х = π/8 + π/2 n, n ∈Z
Пример 5
6sin2x + 4 sin(π-x) cos(2π-x) = 1.
6sin2x + 4 sinx cosx = 1.
6sin2x + 4 sinx cosx – sin2x – cos2x = 0.
5sin2x + 4 sinx cosx – cos2x = 0.
Т.к. cos2x ≠0, то 5tg2x + 4 tgx –1 = 0
Замена: tg x = у.
5у2 + 4у – 1 = 0
D = 16 + 20 = 36
у1 = 1/5 или у2 = –1
tg x = 1/5 или tg x = –1
tg x = 1/5: х = arctg1/5 + πn, n ∈Z
tg x = –1: х = arctg(–1) + πn, n ∈Z
х = –π/4 + πn, n ∈Z
Контрольные вопросы и задания для самостоятельного решения по разделу 7
Ответьте на вопросы:
1) Какое уравнение называется тригонометрическим?
2) Какое уравнение называется однородным первой степени?
3) Какое уравнение называется однородным второй степени?
Решите упражнения:
1)  2)
2) 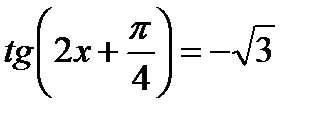
3)  4)
4) 
5) 
6) 
7) 
8) 
9) 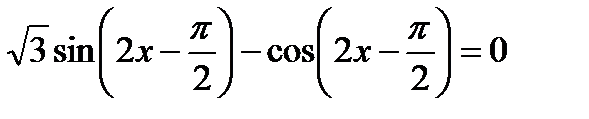
10) 
11) 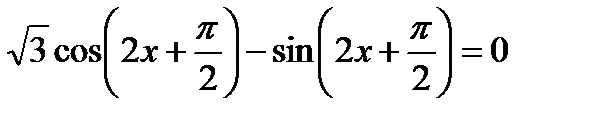
12)  13)
13) 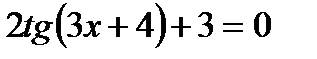
14)  15)
15) 
16)  17)
17) 
18)  19)
19) 
Проверьте своё решение:
Ответы:
1)  2)
2) 
3) 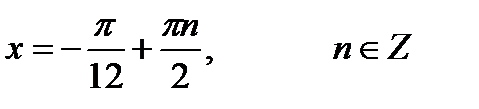 4)
4) 
5)  6)
6) 
7)  8)
8) 
9)  10)
10) 
11) 
12) 
13) 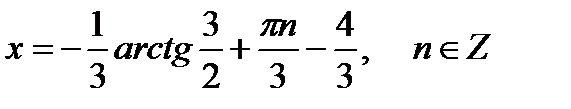
14) 
15) 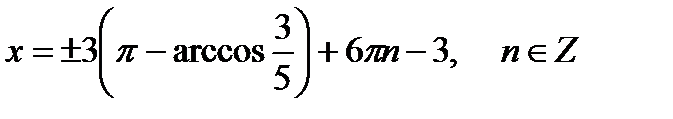
16)  17)
17) 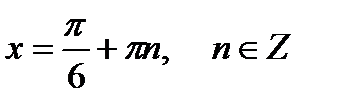
18) 
19) 






