Товар подешевел на 20%. На сколько процентов больше можно купить товара за те же деньги?
Решение:
Товар подешевел на 20%.Следовательно, весь ранее купленный товар можно было бы купить истратив 80% денег, а на оставшиеся 20% можно купить еще 
часть товара, что составляет 25%.
Ответ: на 25%
Задача 11: Сушеные грибы. Влажность свежих грибов - 99%, сушёных - 98%. Как изменился вес грибов после подсушивания?
Решение:
Пусть вес свежих грибов 100 х кг, тогда вес сухого вещества в них х кг. После подсушивания, вес сухого вещества не изменился и стал составлять 2% (на одну пятидесятую) от веса грибов. Вес сухих грибов – 50 х кг, а значит уменьшился в два раза.
Ответ: уменьшился в два раза.
Задача 12: На конференции. 85% делегатов конференции знают английский язык, а 75% - испанский. Какая часть делегатов знает оба языка?
Решение:
Заметим, что 85%+75% = 160%, что на 60% превышает общее число делегатов конференции. За счет кого образовался излишек? За счет тех людей, которые знают оба языка - их мы посчитали дважды. Таким образом, оба языка знают не менее 60% делегатов конференции.
Ответ: не менее 60%.
Задача 13: На туристском слете собрались все участники двух туристических походов (некоторые были в двух походах, некоторые только в одном). В первом походе было 60% мужчин, во втором - 75%. Докажите, что на встречу пришло не меньше мужчин, чем женщин.
Решение:
Пусть в первый поход ходило а человек, а во второй b человек. Тогда, в первый поход ходило 0,6 а мужчин и 0,4 а женщин, а во второй - 0,75 b мужчин и 0,25 b женщин. При этом, количество женщин не превышает 0,4 а + 0,25 b, а количество мужчин не меньше, чем наибольшее из чисел 0,6 а и 0,75 b. Пусть 0,6 а >0,75 b. Тогда 0,6 а >0,4 а +0,25 b (так как 0,2 а >0,25 b). Случай, когда наибольшее - 0,75 b, разбирается аналогично
Задача 14: Морская вода содержит 5% соли. Сколько килограммов пресной воды надо добавить к 40 кг морской воды, чтобы держание соли составляло 2%?
Решение:
. В 40 кг морской воды содержится 40·0,05 = 2(кг) соли, что в новом растворе составляет 2%, следовательно, раствора должно быть 2:0,02 = 100 (кг).
Ответ: следует добавить 60 кг пресной воды.
Задача 15: Вера и Аня посещают математический кружок, в котором больше 91% мальчиков. Найти наименьшее возможное количество участников кружка.
Решение:
.Пусть х - число участников кружка, а у - число девочек. Тогда, согласно условиям задачи, 0,09 x > y или 9 х >100 у, где х и у - натуральные числа. Решая задачу перебором, убедимся, что наименьшее возможное решение при у =2 достигается при х =23. Таким образом, в кружке не менее 23 человек.
Ответ: в кружке не менее 23 человек.
Задача 16: Объём строительных работ увеличивается на 80%. На сколько процентов нужно увеличить число рабочих, если производительность труда будет увеличена на 20%?
Решение:
1) 100% + 80% = 180 = 1,8 (объём строительных работ по сравнению с первоначальным).
2) 100% + 20% = 120 = 1,2 – производительность труда по сравнению с первоначальной.
3) 1,8: 1,2 = 1,5 = 150% - составляет количество рабочих, необходимых теперь по сравнению с первоначальным, т.е. на 50% надо увеличить число рабочих.
Ответ: на 50%
Задача 17: В бассейн проведена труба. Вследствие засорения её приток воды уменьшился на 60%. На сколько процентов вследствие этого увеличится время, потребное для заполнения бассейна?
Решение:
1) 100% - 60% = 40% = 0,4 – такую часть составляет оставшийся приток воды.
2) 1: 0,4 = 2,5 (раза) – во столько раз увеличится время, необходимое для наполнения бассейна, т.е. увеличится на 150%
Ответ: на 150%.
Задача 18: Заработок рабочего повысился на 20%, а цены на продукты и другие товары снизились на 15%. На сколько процентов рабочий теперь на свой заработок может купить больше продуктов и товаров, чем прежде?
Решение:
Примем для простоты вычислений прежний заработок рабочего за 10 руб., и пусть он покупает только один какой-то продукт по 1 руб. за килограмм, т.е. 10 кг. После повышения на 20% заработок рабочего стал 12 руб., а цена продукта после снижения цены на 15% - 0,85 руб. за 1 кг. Теперь рабочий может купить уже 12: 0,85 
14,1 кг, т.е. на 4,1:10 = 0,41 = 41% больше, чем прежде.
Ответ: на 41%.
Задача 19: На утреннем концерте 40% всех посетителей были школьники, 36% - женщины и остальные посетители – мужчины. На вечерний концерт пришло мужчин на 75 % больше, чем на утренний, женщин на 37,5% больше, а школьников на 75% меньше, чем на утренний концерт. Как и на сколько процентов число посетителей на вечерний концерт изменилось по сравнению с числом посетителей на утреннем концерте?
Решение:
1) 40% + 36% = 76% - составляют женщины и дети.
2) 100% - 76% = 24% - составляют мужчины.
3) 24% + 24% 
= 42% - составляют мужчины на вечернем концерте.
4) 40% - 40% = 10% - составляют школьники на вечернем концерте.
5) 36% + 36% 
= 49,5% - составляют женщины на вечернем концерте.
6) 42% + 49,5% + 10% = 101,5% от числа посетителей на утреннем концерте составляет число посетителей на вечернем концерте, т.е. на вечернем концерте посетителей было больше, чем на утреннем, на 1,5%.
Ответ: на вечернем концерте посетителей было больше, чем на утреннем на 1,5%.
Задача 20: 5 литров сливок с содержанием жира 35% смешали с 4 литрами 20-процентных сливок и к смеси добавили 1 литр чистой воды. Какой жирности получилась смесь?
Решение:
1) 5 · 0,35 = 1,75 (л) жира в 5 л сливок.
2) 4 · 0,2 = 0,8 (л) жира в 4 л сливок.
3) 1,75 + 0,8 = 2,55 (л) жира в смеси.
4) 5 + 4 + 1 = 10 (л) – вес смеси.
5) 2,55: 10 = 0,255 = 25,5% - жирность смеси.
Ответ: 25,5%.
Задача 21: Когда 40 рабочих цехавключились в молодёжную бригаду, продукция цеха увеличилась на 20%; когда же 60% всех рабочих цеха стали работать по-новому, продукция цеха увеличилась в 2,5 раза. Сколько рабочих в цехе и во сколько раз увеличится продукция цеха, когда все рабочие станут передовиками производства?
Решение:
1) 250% - 100% = 150% - на столько процентов увеличится продукция.
2) 40 рабочих увеличивают продукцию на 20%
х рабочих увеличивают продукцию на 150%
3) 
рабочих увеличивают продукцию на 150%, они же составляют 60% числа всех рабочих.
4) 300: 0,6 = 500 рабочих было в цехе.
5) 500 рабочих – увеличение на у %
300 рабочих – увеличение на 150%
у = 250%
6) 250% + 100% = 350%, т.е. продукция увеличилась бы в 3,5 раза.
Ответ: 500 рабочих, продукция увеличилась бы в 3,5 раза.
Задача 22: Цена за вход на стадион 150 руб. с человека. Когда цену понизили, количество посетителей увеличилось на 50%, а сбор увеличился на 25%. На сколько рублей понижена плата?
Решение:
Входная плата за двух человек была 300 руб., теперь вместо каждых двух человек стадион посещают трое (число посетителей увеличилось на 50%) и платят 300 + 75 = 375 рублей (общий сбор увеличился на 25%), т.е. один билет стоит теперь 125 руб. (375: 3), значит, плата понижена на 25 руб.
Ответ: на 25 рублей.
Задача 23: За 1 квартал завод выполнил 26% годового плана, а количество продукции, выполненное за 2, 3 и 4 кварталы, пропорционально числам 6,5:7,8:9,1. Определить, на сколько процентов перевыполнил завод план, если во 2 квартале завод дал продукции в 
раза больше, чем в первом.
Решение:
2: 3: 4 = 6,5: 7,8: 9,1 = 5: 6: 7
1) 26% 
= 32,5% годового плана дал завод во втором квартале.
2) 32,5%: 5 = 6,5% приходится на 1 часть.
3) 6,5% · 6 = 39% дал завод в 3 квартале.
4) 6,5% · 7 = 45,5% дол завод в 4 квартале.
5) 26% + 32,5% + 39% + 45,5% = 143% годового плана фактически выполнил завод, т.е перевыполнил план на 43%.
Ответ: на 43%.
Задача 24:. Имеются два куска сплава меди и цинка с процентным содержанием меди р % и q % соответственно. В каком отношении нужно взять эти сплавы, чтобы, переплавив взятые куски вместе, получить сплав, содержащий r % меди?
Решение:
Если первого сплава взять х кг, а второго у кг, то
(кг меди) + 
(кг цинка),
(кг меди) + 
(кг цинка),
В получающемся сплаве будет
(кг меди),
а вес этого сплава будет равен (х + у) кг. Поэтому новая концентрация меди в сплаве по определению будет равна
Согласно условию задачи, полученная дробь равняется 
. Приходим к уравнению
(1)
Повторим ещё раз, в чем состоял способ решения этой задачи. С помощью известных значений концентраций мы «расщепили» сплав на чистые компоненты, а затем, в соответствии с условием задачи, составили новый сплав, подсчитав отдельно весовой баланс каждой компоненты.
Решим полученное уравнение. В этом уравнении два неизвестных, х и у. Поэтому оба неизвестных найти нельзя. Но в этом и нет необходимости, так как достаточно определить не сами величины х и у, а их отношение!
После очевидных преобразований из уравнения (1) получим соотношение
(2)
Рассмотрим несколько случаев.
1. Пусть р = r = q, x · 0 = у · 0.
В этом случае концентрации всех сплавов одинаковые и уравнение (2) показывает, что имеется бесконечное множество решений. Можно взять сколько угодно первого сплава и сколько угодно второго сплава.
2. Пусть 
, x · 0 = у (r – q), х – любое, у = 0.
Смысл этого решения понятен — второго сплава вообще не требуется.
3. Пусть 
, 
. Тогда 
Полученное отношение будет давать решение задачи в общем случае (разумеется, если значение r заключено между значениями р и q, иначе 
окажется отрицательной величиной, что лишено смысла).
Ответ:
Задача 25: Определить процентное содержание спирта в растворе, полученном при смешивании пяти литров 20 %-го и шести литров 35 %-го растворов спирта.
Решение:
Количество «чистого» спирта в первом растворе равно 0,2 · 5 л, а во втором растворе — 0,35 · 6 л. При смешивании общее количество спирта не изменилось (а объём нового раствора равен 5 + 6 = 11 л). Поэтому можно записать уравнение для объёмной концентрации х спирта в полученном растворе
0,2 · 5 + 0,35 · 6 = х · 11,
откуда 
. Процентное содержание равно 
или 
%.
Ответ: %.
Задача 26: От двух однородных кусков сплава с различным процентным содержанием меди, весящих m и п кг, отрезано по куску равного веса. Каждый из отрезанных кусков был сплавлен с остатком другого куска, после чего процентное содержание меди в обоих кусках стало одинаковым. Сколько весили отрезанные куски?
Решение:
Обозначим через р и q — концентрации меди в первом и во втором кусках соответственно, а через х — вес каждого отрезанного куска. Тогда в остатке первого куска содержится (т — х) р кг меди, в остатке второго куска содержится (п — x) q кг меди. После того, как куски снова сплавили, в первом куске оказалось (m — x)p + xq кг меди, а во втором (п — x)q + xp кг меди. Приравнивая концентрации меди в обоих кусках, получим уравнение
или
тпр — хп(р — q) = mnq + xm(p — q),
или
тп(р -q) = х(р - q)(m + п).
По условию задачи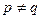 
, следовательно,
Ответ:
Задача 27: В сосуде объёмом V содержится р %-ный раствор соли. Из сосуда выливается а л смеси и доливается а л воды, после чего раствор перемешивается. Эта процедура повторяется п раз. Определить концентрацию соли в растворе после п процедур.
Решение:
Первоначальное количество соли в растворе равно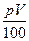 
. После того, как вылили а л смеси, соли осталось
,
а её концентрация после добавления а л воды стала равна
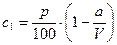
После того, как отлили ещё а л смеси (уже концентрации c 1), в растворе осталось соли
а её концентрация после добавления воды стала равна
Теперь не составляет труда заметить, что после п переливаний концентрация соли в растворе будет определяться формулой
(3)
Ответ:
Задача 28: Концентрация соли уменьшилась в пять раз после 10 переливаний (рассмотренных в предыдущем примере). Какую часть объёма V сосуда составляют а л?
Решение:
Воспользовавшись формулой (3), запишем условие задачи в виде уравнения
,
откуда находим
Ответ:
Задача 29: Сберкасса выплачивает ежегодно 3% от положенного на сберегательную книжку вклада. Через сколько лет текущая сумма будет превышать первоначальную более чем в 2 раза?
Решение:
Пусть начальная величина вклада составляет А рублей. Согласно условию задачи запишем уравнение
,
откуда получаем
Следует отметить, что величина х является иррациональным числом. Но в условии задачи речь идёт о целом числе лет, поэтому, чтобы записать ответ, требуется найти наименьшее натуральное п такое, что 
Ответ: Через 23 года.
Задача 30: В течение трёх лет вкладчик имел одинаковый процент прибыли по отношению к каждому предыдущему году, а затем в течение двух лет в результате инфляции нёс убытки ежегодно в половине процентов по сравнению с процентами прибыли. При какой исходной процентной ставке, не превышающей 200% годовых, вкладчик будет иметь наибольшую итоговую прибыль за пять лет и какова она (по отношению к первоначальному вкладу)?
Решение:
1) Пусть исходная процентная ставка равна х%.
2) Используем формулу сложных процентов, которая позволяет вычислить, каким станет первоначальный вклад а через п лет при проценте прибыли р %. Этот результат равен
.
3) Тогда через три года сумма вкладчика будет равна 
. Так как в течение следующих двух лет вклад уменьшался на 
, то по истечении пяти лет сумма будет такой:
.
4) Рассмотрим функцию 
= , где 
. Исследуем её на наибольшее значение.
.
Критические точки: х = -100 (не входит в область определения), х = 200, х = 80.
; 
;
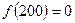5) Таким образом прибыль составляет 109,953%
Ответ: 109,953%
Задача 31:. Курс рубля по отношению к доллару (то есть цена одного рубля в долларах) падает на 4% в квартал. У клиента банка есть два альтернативных варианта помещения денег. По первому варианту он может положить деньги на рублевый чет с начислением 120% в конце года. По второму варианту он может обменять рубли на доллары и положить деньги нa валютный счет с ежемесячным начислением 6% от текущей суммы. На сколько процентов больше или меньше окажется рублевый счет по отношению к валютному через год? При расчетах считать одинаковыми обменные курсы покупки и продажи доллара. (Ответ представить в виде арифметического выражения.)
Решение:
1) Пусть клиент имел а рублей, которые он положил на рублевый счет. Тогда через год у него на счету окажется 2,2 а рублей.
2) Если он обменяет а рублей на b долларов, то в конце года у него на счету окажется 
, т.е. 
.
3) Поскольку курс рубля по отношению к доллару падает на 4% в квартал, то рублевая сумма будет представлена так:
.
4) Сравним увеличение вкладов в рублях и долларах.
Следовательно, сумма в долларах увеличилась на 101,2%
5) Следовательно сумма в рублях увеличилась на 86,9%
6) 101,2 – 86,9 = 14,3%
Ответ: 14,3%
Задача 32:Маклер после одной удачной сделки имел некоторый процент прибыли от вложенного исходного капитала, а затем понес такой же процент убытков со всего, что заимел. После третьей (также неудачной) сделки процент убытков возрос в 4 раза по отношению к проценту прибыли после первого года. При каком исходном проценте такая деятельность маклера приведет к наибольшим возможным долгам и каковы они по отношению к первоначальному капиталу?
Решение:
1) Пусть исходный процент прибыли составляет х%.
2) Тогда, если исходный капитал составлял а единиц, то после первого года сумма стала равна 
.
3) После тех же процентов убытков сумма стала равна
4) После третьей сделки сумма стала равна
.
5) Рассмотрим функцию 
и найдём её наименьшее значение при 
.
.
Найдём критические точки.
; х = -50 (не входит в область определения).
- точка минимума. В этой точке функция принимает наименьшее значение.
6) Таким образом, долги маклера составляют 
первоначальной суммы. Найдём долги в процентах: а – 100%;
; 
Ответ: 93,83%
Задача 33: Зарплата рабочего за месяц составила 8000 рублей. 20% из этой суммы ушло на оплату коммунальных платежей. 5% оставшейся суммы ушло на оплату долга. Сколько денег осталось после этого у рабочего?
Решение:
1) На оплату коммунальных платежей ушло денег:
(руб.)
2) Осталось денег: 8000 – 1600 = 6400 (руб.)
3) На оплату долга ушло 5% от 6400, или
(руб.)
4) После этого осталось денег: 6400 – 320 = 6080 (руб.)
Ответ: 6080 рублей
Задача 34: В двух ёмкостях разного объема содержатся смеси двух веществ: А и В. Вещество В занимает в первой и второй ёмкостях соответственно 70% и 60% от объема. Вес вещества А емкости совпадает с весом вещества В во второй, а вес вещества А во второй ёмкости в 3,5 раза больше веса вещества В в первой ёмкости. Какой процент по весу составляет вещество А, содержащееся в обеих ёмкостях, от суммарного веса содержимого ёмкостей?
Решение:
1) Пусть х – объём первой ёмкости, а у – объём второй ёмкости, а U и V – плотности веществ соответственно.
2) Тогда вес вещества А в первой ёмкости составить 
, а вес вещества В там же - 
.
3) Аналогично во второй ёмкости содержится (по весу) 
вещества А и 
вещества В.
4) Требование задачи приводит к системе уравнений (1) – (2)
5) В задаче требуется найти величину
,
которая после деления числителя и знаменателя на 
примет вид
,
и для её нахождения из системы надо найти величины 
.
6) А) для нахождения величины можно разделить левую часть (1) на левую часть (2), и также поступить с правыми частями.
Получим
,
(второе значение 
противоречит физическому смыслу величины).
Б) Для нахождения величины 
разделим левую часть (1) на правую часть (2), а правую часть (1) на левую часть (2), получим соотношение
.
7) Подставляя найденные величины в выражение для Т, окончательно получим
Ответ: 
Задача 35: Имеется 3 слитка. Первый слиток имеет массу 5 кг, второй 3 кг, и каждый из этих двух слитков содержит 30% меди. Если первый слиток сплавить с третьим, то получится слиток, содержащий 56% меди, а если второй слиток сплавить с третьим, то получится слиток, содержащий 60% меди. Найти вес третьего слитка и процент содержащейся в нём меди.
Решение:
Прежде всего следует предложить учащимся представить условие задачи в виде таблицы:
| № слитка | Вес слитка, кг | Содержание меди, % | Содержание меди, кг |
| |||
| |||
| х | у | 
|
4столбик заполняется после введения двух неизвестных:
х кг – вес третьего слитка;
у % - процентное содержание меди в третьем слитке.
Исходя из этого заполняется последняя строчка в 4-м столбике. Запишем, используя понятие пробы, систему двух уравнение с двумя неизвестными:
Решая её получим: х = 10, у = 69.
Ответ: вес третьего слитка – 10 кг, процентное содержание в нём меди – 69%.
Задача 36: Сколько серебра 500 и 800 пробы нужно сплавить, чтобы получить 225 г. серебра 720 пробы?
Решение:
Способ
х г – вес первого сплава,
у г – вес второго сплава,
х + у = 225 (1)
Для составления второго уравнения целесообразно воспользоваться определением пробы:
, 
Тогда
Получаем следующую систему уравнений:
Решая её, находим: х = 60, у = 165
2 способ:
При помощи рассуждений.
Предполагаем, что в сплав мы взяли только серебро 500 пробы. Тогда в 225 г сплава чистого серебра будет 162 г, что на 49,5 г меньше требующегося количества. Эта разница получилась из-за того, что не был учтен сплав серебра 800 пробы.
В самом деле, в каждом грамме сплава 800 пробы содержится 0,8 г чистого серебра, а в каждом грамме сплава 500 пробы содержится 0,5 г чистого серебра. Следовательно, взяв только сплав 500 пробы, мы с каждого грамма серебра 800 пробы не учли 0,8 -0,5 = 0,3 г чистого серебра,
Таким образом, при получении 225 г сплава 720 пробы не было учтено 49,5: 0,3 = 165 (г) серебра 800 пробы. Итак, для составления сплава, требующегося в задаче, надо взять серебра 800 пробы 165 г, а серебра 500 пробы – 60 г.
Ответ: 165 г, 60 г.
Задача 37: Имеется три сплава. Первый сплав содержит 10% кобальта и 90% железа, второй – 40% железа и 60% никеля, третий – 20% кобальта, 50 % железа и 30% никеля. Из этих сплавов необходимо создать новый сплав, содержащий 20% никеля. Какое наименьшее и какое наибольшее процентное содержание железа может быть в новом сплаве?
Решение:
Пусть х + у + z – масса нового сплава.
; 
.
Подсчитаем значения на границах
При z = 0 
При y = 0 
Так как производная функции 
отрицательна, то функция монотонно убывает в области 
и наибольшее значение достигается при 
, что соответствует 
, а наименьшее значение при 
, что соответствует значению 
.
; 
; 
;
Ответ: 
; 
Задача 38: Через 40 минут после выезда из пункта А автомобиль уменьшил скорость на 20% и через некоторое время прибыл в пункт В. При этом оказалось, что на вторую половину пути он затратил на 5 минут больше, чем на первую. За какое время автомобиль проехал путь от А до В?
Решение. Пусть S (км) - расстояние АB, v (км/ч) – начальная скорость автомобиля. Тогда автомобиль проехал расстояние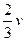 
(км) и уменьшил скорость до 0,8 
. Для вычисления времени, затраченного на первую и на вторую половину пути, необходимо рассматривать два случая.
1) Изменение скорости произошло на первой половине пути, т.е. 
. Тогда из условия задачи получаем уравнение:
Это уравнение решений не имеет, то есть этот случай не может реализоваться.
2) Изменение скорости произошло на второй половине пути, то есть 
. Тогда из условия задачи получим уравнение в виде
Решая это линейное относительно 
уравнение, после очевидных вычислений получим 
, что подходит по условию рассмотрения этого случая 
.
Так как время движения по первой половине пути 
(час), а время движения на второй половине пути по условию больше на 
(час), то всё время движения
(час) = 65 (мин)
Ответ 65 минут.
Задача 39: Имеются слитки трёх типов. Один слиток первого типа весит 5 кг и содержит 30% меди, 20% серебра и 50% золота. Один слиток второго типа весит 2 кг и содержит 40% меди, 30% серебра и 30% золота, а один слиток третьего типа имеет массу 1 кг и содержит 50% меди, 20% серебра и 30% золота. Какое минимальное количество слитков каждого типа потребуется, чтобы, не разрезая их, получить сплав, содержащий 37% меди, 23% серебра и 40% золота?
Решение:
Составим таблицу, в которую внесем концентрации компонентов в слитках, массы слитков и количество слитков, необходимое для получения сплава нужного состава.
| 
| 
| масса | Кол-во | |
| 0,3 | 0,2 | 0,5 | k | ||
| 0,4 | 0,3 | 0,3 | l | ||
| 0,5 | 0,2 | 0,3 | m | ||
| 0,37 | 0,23 | 0,4 |
Полная масса нового сплава равна 5 k + 2 l + т. Составим уравнения материального баланса
Cu: 
Ag: 
Au: 
Упрощая которые получим:
Видно, что третье уравнение является суммой двух первых, так что независимых уравнений всего два. Из двух последних уравнений исключим k и получим 
, откуда 
, m = 4t, где 
. Подставляя в последнее уравнение, найдем
k: k = 2t. Наименьшие значения достигаются при t = 1: k = 2, 1 = 3. т = 4.
Ответ: Наименьшие значения достигаются при t = 1: k = 2, 1 = 3. т = 4.
Задача 40: Партия телевизоров проходит испытание на долговечность. После первого года работы отказало 15 телевизоров, а после второго – ещё 4. сколько телевизоров было исправно после первого года работы, если известно, что отношение числа телевизоров, исправных к концу второго года, к числу телевизоров, исправных к началу года, на 8,75% больше, чем такое отношение, составленное для первого года испытаний?
Решение:
Обозначив через х число телевизоров, исправных после первого года работы, записать условие задачи в виде
Далее получить уравнение:
, откуда 
, 
.
Ответ: 120 телевизоров.
Задача 41: В первом сосуде содержится 5 кг, во втором – 10 кг 5%-го раствора соли. Из каждого сосуда выпарили часть воды, после чего концентрация соли в первом сосуде составила 
, во втором - 
. Известно, что 
. Какое наибольшее и какое наименьшее количество воды могло испариться из обоих сосудов вместе?
Решение:
Количество испарившейся воды
;
(max)
М (5) = 8; М (25) = 4; 
Ответ: 
кг; 
кг.
Заключение.
В данном пособии изложены некоторые понятия теории процентов. Приведены типовые задачи по данной теме. К задачам даны решения. Эта система подобранных упражнений даёт возможность творчески подходить к повторению темы «Текстовые задачи на проценты».
Умение учащихся находить процент от числа, изменение величины в процентах, число по его проценту и т.д. позволяет усложнить текстовые задачи, что развивает логическое мышление.
В результате применения данной системы упражнений по данной теме повышается интерес к математике, увеличивается скорость вычислительных навыков на проценты. Уменьшается количество ошибок при решении сложных задач на проценты. Идёт более глубокое усвоение знаний по теме «Проценты».
Список использованной литературы
- Альхова З.Н., Макеева А.В. Внеклассная работа по математике. Саратов, изд. «Лицей», 2001.
- Вступительные экзамены по математике в Уральском университете в 1991 году. Екатеринбург, 1992.
- Вступительные экзамены по математике в Уральском Государственном университете в 2000 году. Екатеринбург, изд.Уральского университета, 2000.
- Задачи с параметрами. Текстовые задачи. Пособие для поступающих в УГТУ-УПИ. Екатеринбург, 1998
- Зубелевич Г.И. Сборник задач московских математических олимпиад. М.,Просвещение, 1971.
- Математика. Варианты билетов вступительных экзаменов в УГТУ. Решения и ответы. Екатеринбург, 1999, 2000, 2001.
- Назаретов А.П. Конкурсные задачи по математике для поступающих в ВУЗы. М.,2001
- Потапов М.К., Олехник С.Н., Нестеренко Ю.В. Конкурсные задачи по математике. М., 1995.
- Пчелинцев Ф.А., Чулков П.В. Математика 5-6 класс. Уроки математического мышления. М., 1998.
- Чекмарев Я.Ф. Методика преподавания арифметики в 5 и 6 классах. М.,Просвещение, 1965.
- Роль задач в формировании математических знаний и развитии учащихся. Учебное пособие. Екатеринбург, 1993.
- Черкасов О., Якушев А. Математика. Интенсивный курс подготовки к экзамену. М., 2002.
