Процентным отношением двух чисел называется их отношение, выраженное в процентах.
Прежде чем решать задачи на процентное отношение чисел, необходимо повторить с учащимися все, что им известно об отношении чисел. Для этого даются устные примеры и задачи, на которых учащиеся повторяют свойства и преобразования отношений.
Примеры:
1) Сократить отношения: 42: 11,2; 6,8: 5,1.
2) Заменить отношения дробей отношениями целых чисел:
0,25: 0,2; 3,5: 0,21;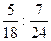 
; 6,3: 14.
3) Найти отношения с точностью
а) до 0,1:
5: 7; 0,8: 1,2; 0,3: 0,8; 1531:
б) до 0,01:
244; 5,1: 21,4; 6: 7.
в) Найти отношения:
6 дм: 4 см; 2,4 км: 40 м
Чтобы перейти к вычислению процентных отношений, даются устные упражнения на небольших числах, при этом употребляются разнообразные формулировки: «Какую часть составляет одно число от другого?» «Каково отношение одного числа к другому?» «Сколько процентов составляет одно число от другого?» и т. д. Вычисляются отношения меньшего числа к большему и большего к меньшему в процентах.
Задача: Сколько процентов составляет число т от а? Отношение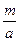 
надо выразить в процентах.
Решение:
1. 
,
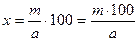2. а ___________100%
т ___________ х
х: 100 = т: а;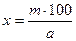 
Следует обратить внимание на некоторые задачи несложного содержания, но требующие вдумчивого отношения при решении.
Задача 1: Время, необходимое для изготовления детали, уменьшилось на 25%. На сколько процентов увеличилась производительность труда?
Решение.
а) Время уменьшается, производительность труда увеличивается
| 100% | 100% |
| 75% | х |
Эти величины обратно пропорциональны, поэтому х: 100 =100: 75; 
; 
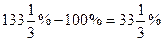
Производительность труда увеличилась на 33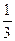 
%.
Задачу можно объяснить иначе.
б) Время изготовления детали примем за 1, оно уменьшилось на 
и стало составлять 
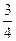единицы. Производительность труда обратно пропорциональна времени и составляет 
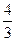первоначальной, т. е. выросла на 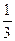, или 33 %.
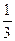Ответ: 33 %.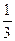
Для избежания ошибок при решении задач на проценты необходимо выяснять в каждом отдельном случае, что принимается за единицу, за целое, за 100%.
Задача 2: Колхоз в первый день весеннего сева засеял 20% всей площади, во второй день 40% оставшегося числа гектаров, в третий день 40% нового остатка. Сколько % всей площади осталось незасеянной?
Решение:
Сначала величина всей площади принимается за единицу или 100%. К концу первого дня осталась незасеянной 100% — 20% = 80% всей площади. Дальше за единицу (100%) принимаются 80% всей площади, из них к концу второго дня засеяли 40%, т. е 
= 32% всей площади, осталось 80% — 32% = 48% всей площади. Эти 48% всей площади принимаем за единицу (100%), из них за третий день засеяли 40%, т. е.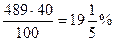 
всей площади, осталось незасеянной
48%-19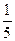 
% = 28 
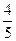% всей площади.
Ответ: 28 %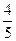
Задача 3: На заводе работают 6250 мужчин и 3750 женщин. Сколько процентов составляет число мужчин и сколько процентов составляет число женщин?
На сколько процентов число мужчин больше, чем число женщин?
На сколько процентов число женщин меньше, чем число мужчин?
Решение:
При решении поставленных вопросов необходимо прежде всего выяснить, какое число при определении процентного отношения принимается за 100%.
1) При решении первого вопроса за 100% принимается все число рабочих (6250 + 3750), хотя в условии задачи указания на это нет. Задача может быть решена различными способами.
Формула решения может быть следующая: 
- процент, числа мужчин на заводе.
Процент числа женщин можно определить решением подобной же формулы или вычитанием: 100% — 62,5% = 37,5%.
2) Второй вопрос ставится для сравнения числа мужчин с числом женщин, которое и принимается за 100%. Необходимо обратить внимание учащихся на то, что при определении процентного отношения словами «чем», «по сравнению с...», «по отношению к...», «от», «к» указывается, какое число следует принять за 100%. Второй вопрос можно решить или
а) определив разность между числом мужчин и женщин и выразив эту разность в процентах от числа женщин, или
б) выразив число мужчин в процентах от числа женщин и определив, на сколько процентов оно больше, чем 100% (женщин).
6250 - 3750 = 2500;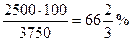 
3) При решении вопроса, на сколько процентов женщин меньше, чем мужчин, число мужчин принимается за 100%, так как с этим числом сравнивается число женщин.
Узнают, насколько женщин меньше, чем мужчин: 6250 – 3750 = 2500; выражают разность 2500 в процентах от числа мужчин:
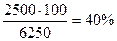
Необходимо обратить внимание учащихся на то, что на вопросы: на сколько процентов число мужчин больше числа женщин и на сколько процентов число женщин меньше числа мужчин, — получились различные ответы, так как разность 6250 — 3750 сравнивалась в одном случае с числом женщин — 3750, в другом случае с числом мужчин — 6250.
Задачи на сплавы и смеси.
При рассмотрении задач на сплавы и на смеси нужно иметь в виду, что математическое описание этих задач строится в предположении: никаких химических процессов, влияющих на количественные соотношения задачи, не происходит.
Перед решением задач важно разъяснить учащимся новое для них понятие "проба сплава". Сплав характеризуется его пробой.
Проба сплава - отношение веса чистого металла к весу сплава, выраженное в промилле или в процентах. Иначе, пробу сплава можно характеризовать числом граммов чистого металла в 1000 г (100 г) сплава. Целесообразно записать в виде формулы:
По содержанию задачи "на сплавы" можно разбить на два основных вида:
1)по характеристикам сплавляемых металлов найти пробу сплава;
2)по известным пробам компонентов сплава, весу и пробе искомого сплава найти вес компонентов сплава.
Характерные компоненты знаний и умений, которыми должны овладеть учащиеся после изучения данной темы:
1. умение выделять и принимать за 100% величину, с которой ведётся сравнение;
2. умение проводить перерасчёты процентов от разных величин в проценты от одной величины;
3. умение представлять условие задачи в рисунках, таблицах, схемах и вести по ним рассуждения;
4. усвоение понятий «процентное отношение», «концентрация».
Примеры решённых задач.
Задача 1:. В марте рабочий выработал 250 000 изделий, из которых 375 изделий второго сорта. В апреле он выработал 300 000 изделий, из которых 360 изделий второго сорта. На сколько процентов снизился выпуск изделий второго сорта?
Решение:
Для сравнения чисел 375 и 360 надо каждое из них выразить в процентах всей выработки («Удельный вес» изделий второго сорта).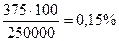 
. 
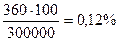. Процент уменьшения удельного веса изделий 2-го сорта: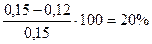 
Ответ: выпуск снизился на 20%.
Задача 2: За два года завод снизил объём выпускаемой продукции на 51%. При этом каждый год объём продукции снижался на одно и то же число процентов. На сколько?
Решение:
Пусть ежегодно выпуск продукции снижался на х %. Примем исходный объём за 1, тогда через год будет выпущено 
, а через два года 
. С другой стороны, выпуск составил 0,49.
= 0,49
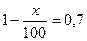
х = 30
Ответ: на 30% в год
Задача 3: Студент М.В.Ломоносов тратил одну денежку на хлеб и квас. Когда цены выросли на 20%, на ту же денежку он приобретал полхлеба и квас. Хватит ли той же денежки хотя бы на квас, если цены ещё раз вырастут на 20%?
Решение:
До повышения цен: денежка = хлеб + квас.
После повышения цен: денежка = (0,5 хлеба + квас) · 1,2.
Из этих уравнений: 2 хлеба = квасу.
Выразим денежку через квас: денежка = 1,5 кваса.
После второго повышения цен: квас · 1,2 · 1,2 = 1,44 кваса.
Значит, денежки хватит на квас.
Ответ: хватит на квас.
Задача 4: Буратино и папа Карло планировали положить свои капиталы на общий счет в банк «Навроде» под 500% годовых, рассчитывая через год забрать вклад величиной 900 золотых. Крах банка изменил их планы. Папа Карло положил свои деньги в банк «Вампириал» под 50% годовых, а Буратино - в банк «Обирон», даже не поинтересовавшись процентной ставкой. Ровно через год они забрали свои вклады. Оказалось, что папа Карло получил 150 золотых, а Буратино - в три раза меньше. Какой процент годовых дает банк «Обирон»?
Решение:
Прибыль в 500% годовых означает увеличение вклада в 6 раз, поэтому у Буратино и папы Карло вначале было 900: 6 = 150 золотых. Прибыль в 50% означает увеличение вклада в 1,5 раза, следовательно, у папы Карло вначале было 150: 1,5 = 100 золотых, а у Буратино 150 - 100 = 50 золотых. После вклада в банк Юбирон» он получил 150: 3 = 50 золотых, т.е. столько же, сколько положил. Таким образом, банк «Обирон» дает 0% годовых.
Ответ: 0% годовых.
Задача 5: Управдом Остап Бендер собрал с жильцов деньги на установку новых квартирных номеров. Адам Козлевич заинтересовался, почему у них в третьем подъезде надо собрать денег на 20% большe, чем во втором, хотя квартир во всех подъездах поровну. Не растерявшись, Остап объяснил, что за двухзначные номера приходится платить вдвое, а за трехзначные - втрое больше, чем за однозначные. Сколько квартир в подъезде?
Решение:
Пусть количество квартир в подъезде равно х. Рассмотрим случаи:
1) х <9;
2) 9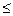 
х< 99;
3) 99 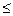х < 999 и т.д. Будем считать стоимость одной цифры равной 1 рублю.
В первом случае стоимость дверных номеров во 2-м подъезде равна сумме стоимости однозначных номеров (9 - х) и стоимости двузначных номеров 2(х - (9 - х)) = З х - 9. А в третьем подъезде в этом случае все номера будут двузначными, и их стоимость равна 2х. По условию задачи
|откуда 4х = 27, что невозможно, т.к. х - целое число.
Во втором случае номера квартир во 2-м подъезде двузначные и трёхзначные, а в 3-м трёхзначные. Стоимость номеров во 20м подъезде будет равна сумме удвоенного количества двузначных номеров 2(99- х) и утроенного количества трёхзначных номеров 3(х – (99 – х)) и это составляет 
стоимости номеров в 3-м подъезде, которая равна 3 х.
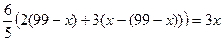
х = 66
Ответ: в подъезде 66 квартир.
Задача 6: Сравните числа. Известно, что 2% положительного числа А больше, чем 3% положительного числа В. Верно ли, что 5% числа А больше, чем 7% числа В?
Решение:
Так как 2% числа А больше, чем 3% числа В, то 4% числа А больше чем 6% числа В, кроме того 1% числа А больше, чем 1% числа В. "Сложив" два последних утверждения, получим, что 5% числа А больше, чем 7% числа В. Или: 0,02А>0,0ЗВ, откуда 0,05А>0,075В>0,07В.
Ответ: верно
Задача 7: Петя купил две книги. Первая из них на была 50% дороже второй. На сколько процентов вторая книга дешевле первой?
Решение:
Вторая книга на треть дешевле первой, то есть на 33 %.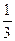
Ответ: на 33 %.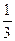
Задача 8: В двух бочках было воды поровну. Количество воды в первой бочке вначале уменьшилось на 10%, а затем увеличилось на 10%. Количество воды во второй бочке, наоборот, вначале увеличилось на 10%, а затем уменьшилось на 10%. В какой бочке стало больше воды?
Решение:
Пусть вначале в каждой из бочек было по х литров воды, тогда в первой бочке, после всех изменений, стало х · 0,9 · 1,1=0,99 х литров воды, а во второй х · 1,1 · 0,9 - то есть тоже 0,99 х: литров воды.
Ответ: поровну.
Задача 9: Где дешевле? В одном магазине; молоко подешевело на 40%, а в другом сначала на 20%, а затем еще на 25%. Где молоко стало стоить дешевле? Первоначальная цена на молоко в каждом из магазинов была одна и та же.
Решение:
Пусть вначале молоко стоило х руб. В первом магазине оно стало стоить на 40% дешевле, то есть 0,6 х руб. Во втором магазине после первого понижения она была 0,8 х, после второго 0,8 х · 0,75 =0,6 х руб. Таким образом, молоко в каждом из магазинов вновь стоит одинаково.
Ответ: одинаково.
