| 100% | а |
| р% | х |
х: а = р: 100
Проверяют формулу, подставляя числовые значения а и р из ранее решенных задач, дальше пользуются формулой для решения задач.
Этот вид задач на проценты решается главным образом нахождением дроби от числа, реже — приведением к единице и очень редко способом пропорций.
Нахождение числа по его проценту
Вторая группа задач на проценты — нахождение числа по его дроби, выраженной в процентах. Эта группа включает 3 вида задач:
1) задачи, в условии которых известно число процентов от числа;
2) задачи, в которых дано число, которое получится, если к данному числу прибавить несколько его процентов;
3) задачи, в которых дано число, получаемое при вычитании из данного числа нескольких его процентов.
Сначала делаются устные упражнения. Даются примеры или задачи с конкретным содержанием.
Задача: найти число, если
1) 1% его равен: 12; 29; 4; 5; 13; 26 и т. д.;.
2) 2% его равны: 36; 84; 9; 6; 24; 8 и т. д.;
3) 3% его равны: 18; 45; 6; 9; 15; 6 и т. д.
Задача: 8% х = 24; найти х.
Решение: выполняется устно с таким объяснением:
8% х или 0,08 числа равны 24, 1% х или 0,01 числа равны 24: 8 = 3; 100% х или все число равно 3*100 = 300.
Этот способ решения — приведением к единице (2-мя действиями).
Задача: 4% х = 12; найти х.
Решение: 4% = 
; х = 12*25==300
(по части, выраженной в процентах находится число)
Решаются задачи, в которые входят и первый и второй вид задач на проценты, например: «Найти число, если 
% его составляют 60% от 120» и т. п.
В числе задач, решаемых устно, должны быть такие, в которых требуется найти число, если даны 10% его, 25%, 50%, 33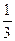 
% и т. п.
Вывод: из устного решения задач и примеров учащиеся делают вывод, что нахождение числа по его процентам есть задача нахождения числа по его части, выраженной в процентах, поэтому решение может записываться, как деление данного числа на дробь.
Письменное решение задач на нахождение числа по его процентам может выполняться двумя действиями или одним действием.
Задача: Техминимум в цехе сдали 150 рабочих, что составляет 75% всего числа рабочих. Сколько рабочих в цехе?
Условие задачи можно записать в виде таблицы.
| 75% | 150 рабочих |
| 100% | х рабочих |
Решение:
а) приведением к единице (двумя действиями)
1%.... 
100%... 
рабочих
б) пропорцией:
х: 150 = 100: 75 (х больше 150 во столько раз, во сколько 100 больше 75).
х = рабочих
Ответ: 200 рабочих
После решения нескольких задач этого вида выводится формула решения в общем виде.
Задача: состоит в нахождении числа (х) по данной величине Р его дроби 
.
Решение:
а) одним действием: 
б) пропорцией
| р% | Р |
| 100% | х |
х: Р = 100: р;
х =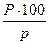 
Подставив в формулу решения числовые значения величин из ранее решенных задач, проверяют формулу и пользуются ею для решения задач
Задача 1. Чтобы наверстать опоздание, скорость поезда увеличили на 35% и тогда она достигла 54 км в час. Какова скорость поезда по расписанию?
Решение.
а) Искомая величина х скорости поезда по расписанию — 100%; увеличенная скорость составляет 100 % + 35% = = 135%. Итак, 135 %х = 54, откуда х = 54:1,35 = 40 (км в час).
б) 
; х = 40 км в час
Ответ: 40 км в час
Задача 2: Трава теряет при высыхании 28% своего веса. Сколько было накошено травы, если из нее получилось 144 ц сена?
Решение.
Вес накошенной травы — 100% (х ц.) Вес сена 100% — 28% = 72%; итак, 72%х == 144 (ц), х = 144 ц: 0,72 = 200 ц = 20 т.
Ответ: 20 т.
