Рекомендации по изучению темы
«Решение текстовых задач на проценты»
 |
Автор: Лапушкина Людмила Григорьевна
учитель математики
ЗМОУ «Средняя общеобразовательная школа №1»
г.Заречный
2005 г.
Содержание
Предисловие. 3
Введение. 4
Процесс решения задачи. 5
1) Нахождение процента от числа. 6
2) Нахождение числа по его проценту. 9
3) Нахождение процентных отношений. 12
Примеры решённых задач. 17
Заключение. 46
Список использованной литературы.. 47
Предисловие.
На уроках математики в школе, а также на вступительных экзаменах в ВУЗы довольно часто предлагаются так называемые текстовые задачи. Одним их видов текстовых задач являются задачи на проценты. Как правило, такие задачи вызывают затруднения у учащихся. Решение задачи способствует развитию логического мышления, сообразительности и наблюдательности, умения самостоятельно осуществлять небольшие исследования.
Цель работы - предложить содержание текстовых задач на проценты. Предложенные задачи – разного уровня сложности. Задачи взяты из различных сборников, а также из вариантов вступительных экзаменов в ВУЗы.
Введение.
Недостаточно лишь понять задачу, необходимо желание решить её. Без сильного желания решить трудную задачу невозможно, но при наличии такового – возможно. Где есть желание, найдётся путь!
Пойя Д.
Работа содержит некоторые рекомендации к изучению темы «Текстовые задачи на проценты». При решении таких задач отрабатываются базовые понятия: что такое процент, нахождение процента от числа и числа по его проценту, процентное отношение, процентное содержание вещества, концентрация раствора, плотность вещества, доля вещества и другие.
Главное при решении текстовых задач – записывать словесные условия при помощи уравнений или неравенств. Для этого необходимо внимательно прочитать условие задачи, чтобы стало понятно её содержание. Затем, при очередном прочтении условия задачи, нужно постепенно вводить неизвестные и сразу записывать связи между известными и неизвестными величинами в виде уравнений или неравенств.
Думаю, что данная работа поможет учителю в подготовке к преподаванию темы, а учащимся самостоятельно овладеть некоторыми навыками решения текстовых задач на проценты.
Процесс решения задачи.
Проценты, «Procentum» - в переводе с латыни обозначают сотую часть числа; изначально появились в Древнем Риме, как термин юридический, именно столько должен был платить должник ростовщику за право пользоваться его деньгами. Сейчас эти понятия применяются не только в банковском деле. Там где речь идёт о статистике, будь то экономика, химия, биология или политология, - везде счёт идёт на проценты.
Нахождение процента от числа
Сначала решаются устные задачи с конкретным содержанием на нахождение процентов от числа, затем числовые примеры.
Задача. Сберкасса дает 2% годовых по бессрочным вкладам и 3% — по срочным. Сколько выплатит сберкасса в год со 100 руб. бессрочного вклада? с 200 руб.? с 3600 руб? по срочным вкладам с 7000 руб.? с 10000 руб.? и т. д.
Решение: Никаких записей, кроме условия, не делается. Учащиеся проводят устные вычисления:
1) 1% от 400 руб. или 0,01 от 400 руб. составляет 4 руб.; 2% или 0,02 составят 8 руб.;
2) 3% от 7000 руб.— 210 руб., так как 1% или 0,01 от 7000 руб. равна 70 руб.
Для выработки вычислительных навыков учащимся даются в большом количестве устные примеры на отвлеченные числа. Помимо общего приема (вычислить 1% делением на 100, потом умножить на число процентов), надо давать в порядке устного счета вычисления 10%, 20%, 25%, 50%, 75%, 33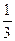 
%, 66 
% от разных чисел и др. Здесь учащиеся должны применять разные приемы устного счета, проявлять сообразительность, изобретательность.
Например: 50% от 8900 составляют 
от 8900, то есть 4450.
10% от 3360 – это 
часть от 3360 то есть 336.
15% от 3360 = 10% от 3360 + 5% от 3360 = 336 + 168 = 504.
9% от 3360 = 10% от 3360 — 1% от 3360 = 336 — 33,6 = 302,4.
60% от 3360 = 50% от 3360 + 10% от 3360 = 1680 + 336 = 2016
Или 60% = 
; от 3360 = 2016.
Учащиеся формулируют общий прием вычисления процентов от числа (деление на 100 и умножение на число процентов) и припоминают, что так решаются задачи на нахождение части от числа. Следовательно, нахождение процентов от числа есть нахождение дроби (части) числа, выраженной в процентах.
Дальше переходят к письменному решению задачи на нахождение процентов от числа.
Так как входящие в эту задачу величины находятся в прямо пропорциональной зависимости, их можно решать способом приведения к единице или способом пропорций, после изучения пропорции и прямой и обратной пропорциональной зависимости.
Задача: Найти 2,5% от 84,8 куб. м.
Записывают условие в виде таблицы:
| 100% | 84,8 куб. м |
| 2,5% | х. |
Решение:
1) 1% от 84,8 м3 = 
куб. м
2,5% от 84,8 м3 = 
куб. м. = 2,12 куб. м.
2) Ту же задачу можно решить способом пропорций.
х: 84,8 = 2,5: 100. Пропорция читается так: х меньше 84,8 во столько же раз, во сколько раз 2,5 меньше 100.
Вывод: Из решения устных примеров учащиеся сделают вывод, что нахождение процентов числа есть вычисление дроби (части) числа, выраженной в процентах.
3) задача может быть решена умножением числа на дробь 0,025 (2,5%), т. е. одним действием:
84,8*0,025 = 2,12 (куб. м).
Ответ: 2,12 куб. м.
После решения достаточного числа числовых задач и примеров можно дать общую формулу решения задач этого вида.
Задача. Найти р% от числа а.
Решение одним действием:
р% = 
; р% от числа 
или 0,01 ар
