Рассмотрим пример решения задачи о равновесии тела под действием плоской системы сил.
Пример.
Определить реакции шарнирных опор А и В балки, находящейся под действием сосредоточенной силы F = 60 Н, равномерно распределенной нагрузки с интенсивностью q = 15 Н/м и пары сил с моментом М = 40 Н·м; расстояние a = 1 м.(рис.1.37).
Рис.1.37
Решение. Введем систему координат Oxy, совместив начало координат О с неподвижным шарниром А и направив ось Ox вдоль балки.
Для определения опорных реакций рассмотрим равновесие балки. К ней приложены активные силы: 
, пара сил с моментом М и равномерно распределенная нагрузка. Заменим распределенную нагрузку эквивалентной сосредоточенной 
, равной по модулю Q = q· 2 a = 30 Н и приложенной в средней точке нагруженного участка.
На балку наложены две связи: неподвижная шарнирная опора в точке А и подвижная шарнирная опора (каток) в точке В. Отбросим мысленно эти связи, заменив их соответствующими реакциями. Реакция 
A неизвестна по величине и направлению, поэтому разложим её на две неизвестные по величине составляющие X A, Y A, направленные по координатным осям. Опора в точке В не препятствует её перемещению вдоль наклонной плоскости и, следовательно, реакцию B следует направить перпендикулярно наклонной плоскости, то есть эта реакция известна по направлению, но неизвестна по величине.
Приведенные выше действия можно назвать составление эквивалентной силовой схемы (рис.1.38).
Таким образом, в задаче имеется три неизвестных скалярных величины: XA, YA, RB. Поскольку для произвольной плоской системы сил имеется три независимых уравнения равновесия, данная задача является статически определимой[7].
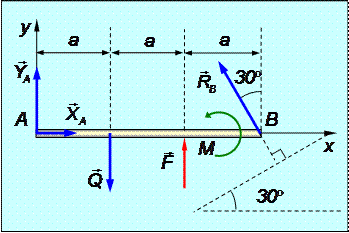
Рис.1.38
Составим уравнения равновесия для полученной эквивалентной силовой схемы.
Эти уравнения равновесия записываются в рассматриваемом примере следующим образом:
,
,
.
Напомним, что алгебраические моменты сил берутся со знаком плюс, если они направлены против хода часовой стрелки. При вычислении момента реакции B относительно точки А выделена её вертикальная составляющая, равная RB cos 30° и имеющая плечо 3 a, а горизонтальная составляющая имеет нулевой момент относительно точки А.
Из третьего уравнения (2) и (3) находим:
RB = (Q - 2F - M / a)/(3cos 30°) 
- 50.0 Н.
Подставив в первое и второе, получим:
ХA=((Q - 2F - M / a)/(3cos 30°))sin30° -25.0 Н,
YA = (2Q - F + M/a)/3 13.3 Н.
Полученные отрицательные значения RB и XA означают, что сила B и составляющая реакции X A противоположны показанным на рис.1.38 направлениям этих векторов.
Величина реакции RA = (XA2 + YA2) 
28.3 Н.
На примере решения рассмотренной задачи сформулируем общие правила решения задач в виде алгоритма решения задач статики:
· Составить силовую схему, выполнив следующее:
- выбрать объект рассмотрения (рассматриваемую механическую систему), отбросив при этом все остальные тела Вселенной;
- заменить влияние отброшенных тел силами, приложенными к точкам рассматриваемой механической системы;
- заменить отброшенные связи их реакциями;
- заменить распределенные нагрузки эквивалентными сосредоточенными силами;
- заменить пары сил их моментами.
· Написать систему уравнений равновесия для составленной силовой схемы.
· Решая полученную систему уравнений, найти неизвестные силы или/и реакции.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Сформулируйте алгоритм решения задач статики.
