ОСНОВЫ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
Электронный учебник по дисциплине: «Теоретическая механика»
Для студентов дистанционной формы обучения
Леготин С.Д., к.т.н., доцент,
Московский государственный индустриальный университет
Москва, 2008
ВВЕДЕНИЕ
Как и в любой естественной теоретической науке, в теоретической механике основным инструментом служит математика, Такой аппарат предполагает использование математической логики при формулировке и решении поставленных задач. Поэтому впредь при определении основных понятий, выводе или формулировке положений теоретической механики, по - возможности, будем использовать математический подход.
Итак, несколько определений.
Механика – наука о движении и взаимодействии материальных тел.
Под движением понимают перемещение в пространстве одних тел относительно других.
Под механическим взаимодействием подразумевают такие действия тел друг на друга, при которых изменяются движения этих тел, либо они сами деформируются (меняют свою форму).
Теоретическая механика - раздел механики, изучающий наиболее общие законы движения и равновесия т.н. «идеальных» материальных объектов, т.е. абстрактных моделей реальных тел.
К ним относятся:
· материальная точка;
· абсолютно твердое тело;
· механическая система - совокупность материальных точек и абсолютно твердых тел, включенных в данное рассмотрение.
Определим эти основные понятия.
Материальная точка – тело, размерами которого можно пренебречь по сравнению с расстояниями до других тел.
Абсолютно твердое тело – тело, расстояния между любыми двумя материальными точками которого не изменяются, как бы оно не перемещалось.
Из последнего определения вытекает, что такое тело – не деформируемое (абсолютно жесткое). Сама же механика – классическая (не релятивистская) механика, т.е. механика, в которой тела двигаются со скоростями, существенно меньшими скорости света.
Свободное тело – то, которому можно сообщить любое перемещение в пространстве. Если перемещение данного тела в пространстве ограничивается другими телами, то его называют несвободным. Тела, ограничивающие движение тела, называют связями.
Теоретическая механика состоит из трех разделов: статики, кинематики и динамики.
Статика – учение о равновесии совокупности тел (механической системы).
Кинематика - часть механики, в которой изучаются описание различных движения материальных точек, абсолютно твердых тел и механических систем, но не рассматриваются причины, вызывающие изменение характера движения.
Динамика - часть механики, в которой рассматривается влияние сил на состояние движения материальных точек, абсолютно твердых тел и механических систем.
Иногда кинематику и статику объединяют в общий раздел, который называется кинетика - наука о механических движениях.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Что такое «абсолютно твердое тело»?
2. Как определяется «материальная точка»?
3. Сформулируйте определение для термина «связь».
Раздел 1. СТАТИКА
Задачей статики является определение условий равновесия материальных тел, находящихся под действием заданной совокупности сил. Под равновесием тела подразумевается его покой относительно некоторой инерциальной системы отсчета (например, системы отсчета, покоящейся относительно Земли).
Введение в статику. Основные положения
1.1.1 Сила. Классификация сил
Определим понятие силы как меры механического взаимодействия материальных тел (более корректно сила определяется в разделе «динамика», где сила определяется по способности вызвать движение тел из состояния покоя или изменить существующее движение последних).
Силу (от английского слова “Force”) принято обозначать большой латинской буквой F, либо другой буквой.
Сила - вектор, при обозначении которого необходимо указывать признаки векторной величины, т.е. указывать надстрочные стрелк у или черту, либо саму букву выделять жирным шрифтом [1]:
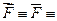F
Указанные здесь обозначения силы эквивалентны, поэтому они объединены символом тождественности «
», или эквивалентности.
Действие силы на тело определяется:
· модулем или абсолютным значением силы (обозначается | 
| F) – это величина силы, выраженная в неких единицах измерения[2];
· направлением силы (ортом[3] e);
· точкой приложения силы (т. A).
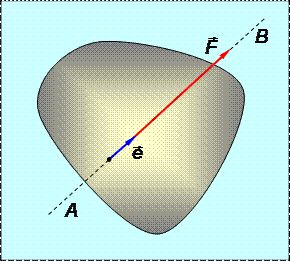
Рис.1.1
Прямая, вдоль которой направлена сила, называется линией действия силы (линия AB, рис.1.1).
Сила может быть задана:
- геометрическим способом, то есть как вектор с известным модулем F и известным направлением, определяемым ортом e;
- аналитическим способом, то есть её проекциями F X, F Y, F Z на оси выбранной системы координат 0xyz.
Проекции силы определяются её модулем и углами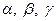 
, которые образует сила с координатными осями 0x, 0y, 0z, следующими соотношениями:
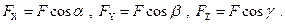
| (1.1) |
Проекция силы на ось равна произведению модуля силы на косинус угла между этой силой и осью.
Модуль силы определяется через свои проекции (рис.1.2), как:
 .
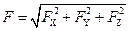| (1.2) |
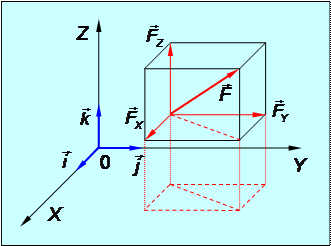
Рис.1.2
Материальные тела могут действовать друг на друга путем непосредственного соприкосновения или на расстоянии. В зависимости от этого силы можно разделить на поверхностные силы, приложенные к поверхности тела (например, силы давления на тело со стороны окружающей среды) и объемные силы, приложенные к данной части тела (например, силы тяготения)
Поверхностные и объемные силы называют распределенными силами. В ряде случаев силы можно рассматривать распределенными по некоторой кривой (например, т.н. «погонный вес», или вес одного метра длины тонкого стержня). Распределенные силы характеризуются их интенсивностью, то есть величиной силы, приходящейся на единицу длины, площади или объема. Интенсивность может быть постоянной (равномерно распределенные силы) или переменной величиной.
Если можно пренебречь малыми размерами области действия распределенных сил, то рассматривают сосредоточенную силу, приложенную к телу в одной точке (условное понятие, так как практически приложить силу к одной точке тела нельзя).
Подытоживая сказанное, можно сформулировать следующую классификацию сил по степени их локализации:
· сосредоточенные силы;
· распределенные силы, в том числе:
- линейно распределенные;
- поверхностные;
- объемные.
По принадлежности к рассматриваемой механической системе силы можно разделить на внешние и внутренние.
Внешними называются силы, которые действуют на это тело (систему) со стороны других тел, внутренними - силы, с которыми части данного тела (данной системы) взаимодействуют друг с другом.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Что такое «модуль силы»?
2. Определите понятие «линия действия силы».
3. Проекция силы на ось – это (….?).
Система сил
Системойсил называют совокупность сил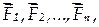 
приложенных к рассматриваемой механической системе (рис.1.3).
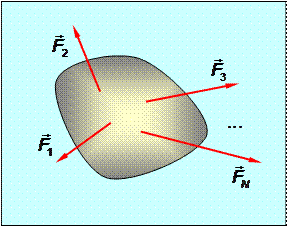
В зависимости от расположения линий действия сил систему сил называют:
· плоской , если линии действия всех сил лежат в одной плоскости;
· пространственной , если линии действия сил не лежат в одной плоскости;
· системой сходящихся сил , если линии действия всех сил пересекаются в одной точке;
· системой параллельных сил , если линии действия всех сил параллельны друг другу.
·
Рис.1.3
Две системы сил называются эквивалентными , если одну систему сил, приложенных к свободному твердому телу, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело.
Система сил называется уравновешенной или эквивалентной нулю, если в результате её приложения к покоящемуся (т.е. находящемуся в равновесии) телу она не сообщает телу никакого движения.
Если система сил эквивалентна одной силе, то эта сила называется равнодействующей силой данной системы сил (обычно обозначаемой 
).
Сила, равная по модулю равнодействующей силе, противоположная ей по направлению и действующая вдоль той же прямой, называется уравновешивающей силой.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Что такое «плоская система сил»?
2. Что значит «системы сил эквивалентны»?
3. Любая ли система сил имеет равнодействующую?
Аксиомы статики
Обобщая опыт изучения физических законов природы, Галилей и Ньютон сформулировали основные законы механики, которые могут рассматриваться как аксиомы механики, так как имеют в своей основе экспериментальные факты.
Аксиома 1. Действие на точку твёрдого тела нескольких сил равносильно действию одной равнодействующей силы, строящейся по правилу сложения векторов (рис.1.4).
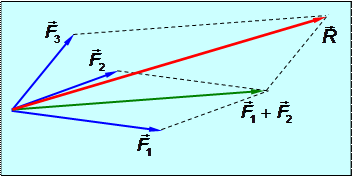
Рис.1.4
Следствие 1. Силы, приложенные к точке твёрдого тела, складываются по правилу параллелограмма: их равнодействующая соответствует диагонали параллелограмма, построенного на этих силах, как на сторонах (рис.1.5).
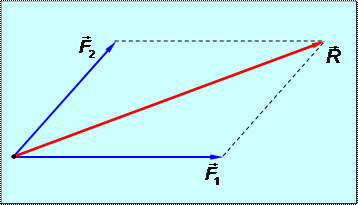
Рис.1.5
Следствие 2. Сложение можно осуществлять по правилу треугольника: их равнодействующая соответствует вектору, начало которого совпадет с началом вектора 
, а конец – с концом вектора 
при условии, что начало совмещено с концом вектора (рис.1.6).
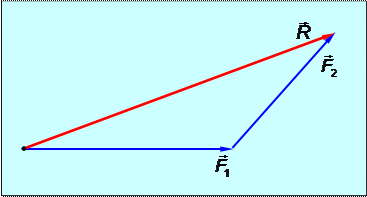
Рис.1.6
Такие сложения обозначаются векторной суммой:
| =+ .
| (1.3) |
.
Модуль равнодействующей может быть вычислен с использованием теоремы косинусов по следующей формуле:
R=(F 1 2+F 2 2+2F 1 F 2 cos  )  ,
| (1.4) |
где - угол между силами и .
Обратная сложению является операция разложения сил.
Если на тело действует сила, то её действие можно заменить несколькими силами, называемыми составляющими.
Замена одной силы несколькими называется разложением силы на составляющие по заданным направлениям.
Для плоской, двухмерной статики чаще всего производят разложение силы на составляющие по двум взаимно перпендикулярным направлениям (рис.1.7). Для объёмной, трёхмерной статики – на три взаимно перпендикулярных направления (см. рис.1.2). Для этого силу проецируют на заданные оси.
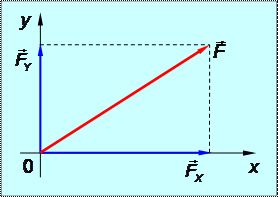
Рис.1.7
Аксиома 2. Система из двух сил, приложенных к абсолютно твёрдому телу, является уравновешенной, если эти силы равны по величине, направлены в противоположные стороны и лежат на одной прямой (рис.1.8).
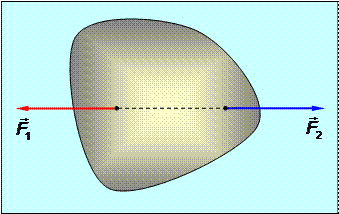
Рис.1.8
Математически такие силы связаны друг с другом соотношением инверсии:
| = -
| (1.5) |
Аксиома 3 . Действие на абсолютно твёрдое тело системы сил не изменится, если добавить (или удалить) к ней уравновешенную систему сил. Это означает, что вновь полученная система сил эквивалентна исходной.
Следствие. Силу, действующую на точку абсолютно твёрдого тела, можно переносить вдоль линии действия силы (т.е. сила является скользящим вектором [4]).
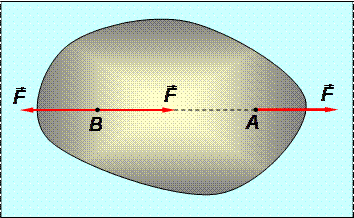
Рис.1.9
Докажем это. Пусть на тело действует сила F, приложенная в точке А (рис.1.9). Приложим в точке В, принадлежащей линии действия силы, уравновешенную систему из двух одинаковых и противоположно направленных сил, также ориентированных вдоль линии АВ и равных по модулю F. Рассматривая две крайние силы из полученной системы трех сил, легко увидеть, что они также образуют уравновешенную систему. Отбросим её, тогда в системе останется только одна сила, приложенная в точке В, равная исходной, что и требовалось доказать.
Аксиома 4 . Действие одного тела на второе равно и противоположно действию этого второго тела на первое (сила действия равна силе противодействия).
Аксиома 5. Связи, наложенные на систему материальных точек, можно заменить силами реакций [5], действие которых эквивалентно действию связей.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Сформулируйте правила сложения сил.
2. Что значит «Сила – скользящий вектор»?
3. Закон равенства действия и противодействия и аксиома 4 - это одно и то же или нет?
Основные операции с силами в статике
В статике вводят некоторые операции над силами, используя которые удается сформулировать решения задачи статики наиболее компактно и удобно.
Эти операции следующие:
- для плоской, или двухмерной статики
· проекция силы на ось;
· алгебраический момент силы;
· алгебраический момент пары сил.
- для пространственной, или трехмерной статики
· проекция силы на плоскость;
· проекция силы на ось;
· векторный момент силы;
· осевой момент силы;
· векторный момент пары сил.
Рассмотрим эти операции отдельно для плоской и пространственной задач.
