Доказано, что для всякого симметрического преобразования 
евклидова пространства, существует базис из собственных векторов, по которому можно построить ортонормированный базис, в котором матрица преобразования будет иметь диагональный вид.
При этом матрица Т, приводящая симметрическую матрицу А к диагональному виду АД, есть матрица перехода от исходного ортонормированного базиса Б0 к ортонормированному базису из собственных векторов БСВ.
Алгоритм приведения симметрической матрицы к диагональному виду таков:
1) Найти собственные числа (корни характеристического уравнения) данной матрицы.
2) Построить ортонормированный базис БСВ из собственных векторов.
3) Составить матрицу Q, столбцами которой являются столбцы координат нормированных собственных векторов – эта матрица приводит данную симметрическую матрицу к диагональному виду.
4) Записать диагональную матрицу, на главной диагонали которой стоят собственные значения исходной матрицы (с учетом их кратности), расположенные в порядке нумерации векторов базиса БСВ из собственных векторов.
Рассмотрим пример.
Пример 7
Привести симметрическую матрицу 
к диагональному виду.
Решение
Будем следовать сформулированному алгоритму.
1. Составим характеристическое уравнение 
. Найдем его корни:
, 
, 
,
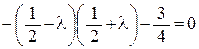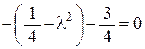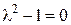откуда 
, 
.
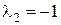Собственные значения 
и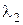 
различны, значит, соответствующие им собственные векторы ортогональны.
2. Найдем координаты собственных векторов из системы
При получим систему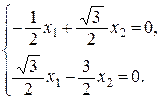 
Решая эту систему, находим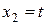 
, 
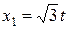, откуда первый собственный вектор и 1 = 
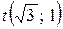, нормировав его, получим е 1 = 
.
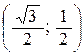При 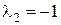получим систему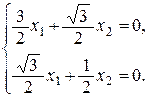 
Решая ее, находим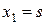 
, 
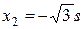, тогда второй собственный вектор и 2 = 
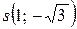, нормировав его, получим е 2 = 
.
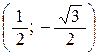Векторы { е 1. е 2} образуют базис БСВ.
3. Запишем о матрицу, приводящую матрицу А к диагональному виду:
Q = 
.
4. Искомая диагональная матрица АД =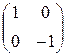 
.
Определение 12
Преобразование : E п ® E п называется ортогональным, если оно сохраняет скалярное произведение двух любых векторов х и у этого пространства, т.е. ( х, у) = (х, у).
Свойства ортогональных преобразований:
1. Ортогональное преобразование является невырожденным.
2. Для каждого ортогонального преобразования существует обратное преобразование, являющееся ортогональным.
3. Произведение двух ортогональных преобразований есть ортогональное преобразование.
4. Ортогональное преобразование не меняет нормы вектора: || х || = || х ||.
5. Ортогональное преобразование не меняет углов между векторами:
( х,^ у) = (х,^ у).
6. Ортогональное преобразование переводит ортонормированный базис в ортонормированный.
7. Матрица ортогонального преобразования в ортонормированном базисе является ортогональной, т.е.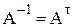 
. И наоборот, если в ортонормированном базисе матрица оператора – ортогональная, то этот оператор – ортогональный.
8. Собственные значения ортогонального преобразования по абсолютной величине равны 1.
Примерами ортогональных преобразований являются:
1) Преобразование поворота плоскости на угол j относительно начала координат, матрица которого в базисе Б0: 
имеет вид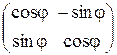 
.
Действительно, пусть х = (х 1, x 2), у = (у 1, у 2), тогда
х = 
,
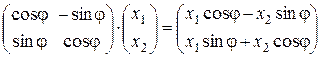у =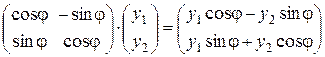 
.
Тогда найдем скалярные произведения (х, у) и ( х, у):
(х, у) = 
,
( х, у)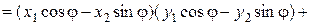 
,
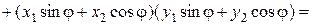
откуда ( х, у) = (х, у), т.е. преобразование поворота плоскости на угол j – ортогональное.
2) Зеркальное отражение точек плоскости от оси ОХ, матрица этого преобразования в базисе Б0: имеет вид .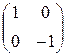
*) Докажите самостоятельно линейность этого преобразования и преобразования из пункта г).
