1. Собственный вектор и линейного преобразования имеет единственное собственное значение l, ему соответствующее.
Доказательство: Предположим, что собственному вектору и соответствует два собственных значения l1 и l2. Тогда 
и = l1 и и и = l2 и, откуда l1 и = l2 и, или (l1 – l2) и = 0. Но т.к. и ¹ 0, то l1 – l2 = 0, откуда l1 = l2. Следовательно, собственное число, соответствующее данному собственному вектору – единственное. ▲
2. Если и – собственный вектор, l – соответствующее ему собственное значение и a ¹ 0 – произвольное действительное число, то a и – также собственный вектор с тем же собственным значением l.
Доказательство: Так как и – собственный вектор с собственным числом l, то и = l и. Поскольку – линейный оператор, то
(a и) = a( и) = a(l и) =l(a и),
следовательно, a и – собственный вектор с собственным значением l. ▲
3. Если и и v – собственные векторы, соответствующие одному и тому же собственному значению l, и и + v ¹ 0, то и + v – также собственный вектор, соответствующий собственному значению l.
Доказательство: Пусть и и v – собственные векторы, соответствующие собственному значению l, причем и + v ¹ 0. Тогда и = l и и v = l v.
Поскольку – линейное преобразование, то
(и + v) = и + v = l и + l v = l(и + v),
значит, и + v – также является собственным вектором, соответствующим собственному значению l. ▲
4. Собственные векторы, соответствующие различным собственным числам, линейно независимы.
Доказательство: Ограничимся доказательством этого свойство для двух векторов. Пусть и и v – собственные векторы, соответствующие собственным значениям l1 и l2, причем l1¹ l2. Предположим, что и и v линейно зависимы, т.е. a и +b v = 0 и a ¹ 0. Тогда и = l v, где l = – 
, а по свойству 2) вектор и = l v есть собственный вектор с таким же собственным числом, что и v, т.е. l2. Но по условию вектор и соответствует собственному числу l1 ¹ l2.
Одному и тому же линейному преобразованию в разных базисах соответствуют подобные, но разные матрицы. Естественно возникает вопрос, существует ли базис, в котором матрица линейного преобразования имеет наиболее простой – диагональный – вид? Справедливо утверждение:
Линейное преобразование : L n ® L n тогда и только тогда задается в базисе Б:{ а 1, а 2, …, а п } диагональной матрицей, когда все векторы этого базиса являются собственными векторами преобразования .
Пусть преобразование в базисе Б имеет матрицу АБ, не являющуюся диагональной. И пусть в рассматриваемом пространстве существует базис БСВ из собственных векторов преобразования , в котором матрица 
преобразования имеет диагональный вид. Тогда из свойства подобия матриц линейного преобразования следует, что
,
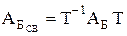где Т – матрица перехода от базиса Б к базису БСВ.
Матрицу А называют приводимой к диагональному виду, если существует невырожденная матрица Т такая, что 
– диагональная матрица. При этом говорят, что матрица Т приводит матрицу А к диагональному виду. Диагональную матрицу преобразования будем обозначать АД.
