Пусть  и
и  – два линейных преобразования линейного пространства L.
– два линейных преобразования линейного пространства L.
Определение 6
Суммой преобразований  и
и  называется преобразование C такое, что " х ÎL C х =
называется преобразование C такое, что " х ÎL C х =  х +
х +  х. Обозначают сумму преобразований C =
х. Обозначают сумму преобразований C =  +
+  .
.
Например, если  :R2®R2 такое, что " х = [ х 1, х 2]ÎR2
:R2®R2 такое, что " х = [ х 1, х 2]ÎR2  х = [ х 1+ х 2, 2 х 2], а
х = [ х 1+ х 2, 2 х 2], а  :R2®R2 такое, что " х = [ х 1, х 2]
:R2®R2 такое, что " х = [ х 1, х 2]  х = [3 х 1, х 1 –2 х 2], то преобразование C =
х = [3 х 1, х 1 –2 х 2], то преобразование C =  +
+  такое, что " х = [ х 1, х 2]ÎR2
такое, что " х = [ х 1, х 2]ÎR2
C х =  х +
х +  х = [ х 1+ х 2, 2 х 2] + [3 х 1, х 1 –2 х 2] = [4 х 1+ х 2, х 1].
х = [ х 1+ х 2, 2 х 2] + [3 х 1, х 1 –2 х 2] = [4 х 1+ х 2, х 1].
Пользуясь определением 6, можно доказать, что сумма линейных преобразований есть линейное преобразование:
C (х + у) =  (х + у) +
(х + у) +  (х + у) =
(х + у) =  х +
х +  у +
у +  х +
х +  у =
у =
= ( +
+  ) х + (
) х + ( +
+  ) у = C х + C у,
) у = C х + C у,
C (a х) =  (a х) +
(a х) +  (a х) = a(
(a х) = a( х) +a(
х) +a( D) = a(
D) = a( х +
х +  х) = a C х.
х) = a C х.
Найдем матрицу С преобразования C =  +
+  .
.
Пусть преобразования  и
и  линейного пространства L в некотором базисе Б имеют соответственно матрицы А и В. Рассмотрим произвольный вектор х ÎL. Обозначим:
линейного пространства L в некотором базисе Б имеют соответственно матрицы А и В. Рассмотрим произвольный вектор х ÎL. Обозначим:
Х – координатный столбец вектора х в базисе Б;
 – координатный столбец образа у A=
– координатный столбец образа у A=  х вектора х при преобразовании
х вектора х при преобразовании  в базисе Б;
в базисе Б;
 – координатный столбец образа у B =
– координатный столбец образа у B =  х вектора х при преобразовании
х вектора х при преобразовании  в базисе Б;
в базисе Б;
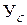 – координатный столбец образа у C = C х вектора х при преобразовании C в базисе Б.
– координатный столбец образа у C = C х вектора х при преобразовании C в базисе Б.
Тогда  = АХ,
= АХ,  = ВХ,
= ВХ, 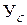 = СХ.
= СХ.
Но, согласно определению преобразования C =  +
+  , имеем:
, имеем:
C х = ( +
+  ) х =
) х =  х +
х +  х,
х,
или, в матричной форме
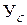 =
=  +
+  = АХ + ВХ = (А + В)Х,
= АХ + ВХ = (А + В)Х,
Получили 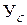 = СХ и
= СХ и 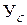 = (А + В)Х, откуда С = А + В. Таким образом, матрица суммы преобразований равна сумме матриц слагаемых.
= (А + В)Х, откуда С = А + В. Таким образом, матрица суммы преобразований равна сумме матриц слагаемых.
Определение 7
Произведением оператора  на число a называется оператор такой C, что C х = a(
на число a называется оператор такой C, что C х = a( х).Обозначается C = a
х).Обозначается C = a  .
.
Например, если  : R2®R2 такой, что " х = [ х 1, х 2]ÎR2
: R2®R2 такой, что " х = [ х 1, х 2]ÎR2  х = [ х 1+ х 2, 2 х 2], то преобразование (
х = [ х 1+ х 2, 2 х 2], то преобразование ( ) определяет вектор
) определяет вектор
у = 3( х) = 3[ х 1+ х 2, 2 х 2] = [3 х 1+3 х 2, 6 х 2].
х) = 3[ х 1+ х 2, 2 х 2] = [3 х 1+3 х 2, 6 х 2].
Докажите, что:
1) Если преобразование  – линейное, то и a
– линейное, то и a  – линейное преобразование.
– линейное преобразование.
2) Матрица преобразования C = a  равна С = aА, где А – матрица преобразования
равна С = aА, где А – матрица преобразования  .
.
Используя операции сложения преобразований и умножения преобразования на число, можно определить операцию вычитания преобразований:
( –
–  ) х = (
) х = ( +(–
+(–  )) х =
)) х =  х –
х –  х.
х.
Матрица такого преобразования, очевидно, равна А – В.
Определение 8
Произведением (композицией) преобразований  и
и  называется преобразование C, определяемое равенством C х =
называется преобразование C, определяемое равенством C х =  (
( х).Обозначается произведение преобразований C =
х).Обозначается произведение преобразований C = 
 .
.
Из определения следует, что умножение преобразований означает последовательное их применение.
Например, если преобразование  :R2®R2 такое, что " х =[ х 1, х 2]ÎR2
:R2®R2 такое, что " х =[ х 1, х 2]ÎR2  х = [ х 1+ х 2, 2 х 2], а преобразование
х = [ х 1+ х 2, 2 х 2], а преобразование  :R2®R2такое, что " х = [ х 1, х 2]ÎR2
:R2®R2такое, что " х = [ х 1, х 2]ÎR2 
 = [3 х 1, х 1 – 2 х 2], то преобразование C =
= [3 х 1, х 1 – 2 х 2], то преобразование C =  .
.  каждому х = [ х 1, х 2]ÎR2 ставит в соответствие вектор
каждому х = [ х 1, х 2]ÎR2 ставит в соответствие вектор
C х =  (
( х) =
х) =  ([3 х 1, х 1 –2 х 2]) = [3 х 1 + (х 1 – 2 х 2), 2(х 1 –2 х 2)] =
([3 х 1, х 1 –2 х 2]) = [3 х 1 + (х 1 – 2 х 2), 2(х 1 –2 х 2)] =
= [ 4 x 1 – 2 x 2, 2 x 1– 4 x 2].
Заметим, что преобразование 
 , вообще говоря, не совпадает с преобразованием
, вообще говоря, не совпадает с преобразованием 
 .
.
Действительно, например, для рассмотренных выше преобразований  и
и  найдем преобразование C1 =
найдем преобразование C1 = 
 :
:
C1 х =  (
( х) =
х) =  ([ х 1+ х 2, 2 х 2]) = [3(х 1 + х 1), х 1+ х 2 – 2(2 х 2)] =
([ х 1+ х 2, 2 х 2]) = [3(х 1 + х 1), х 1+ х 2 – 2(2 х 2)] =
= [ 3 x 1 +3 x 2, x 1– 3 x 2].
Очевидно, C х ≠ C1 х.
Пользуясь определением произведения преобразований, можно рассматривать «п -ю степень» преобразования, как последовательное применение этого преобразования п раз:
 2 х =
2 х =  (
( х),
х),  3 х =
3 х =  (
( (
( х)), и т.д.
х)), и т.д.
Докажите, что если  и
и  – линейные преобразования, то и
– линейные преобразования, то и 
 – линейное преобразование.
– линейное преобразование.
Пусть преобразования  и
и  линейного пространства L в некотором базисе Б имеют соответственно матрицы А и В. Найдем матрицу С преобразования C =
линейного пространства L в некотором базисе Б имеют соответственно матрицы А и В. Найдем матрицу С преобразования C = 
 в этом же базисе. Обозначим:
в этом же базисе. Обозначим:
Х – координатный столбец произвольного вектора х пространства L в базисе Б,
У – координатный столбец вектора  х в этом же базисе,
х в этом же базисе,
Z – координатный столбец вектора  (
( х).
х).
Тогда У = ВХ, Z = АУ, Z = СХ. Отсюда имеем
Z = АУ = А(ВХ) = (АВ)Х и Z = СХ,
значит, С =А.В.
Таким образом, матрица произведения преобразований равна соответствующему произведению матриц преобразований-сомножителей.
Матрица преобразования  п (п – натуральное число) равна, очевидно, А п.
п (п – натуральное число) равна, очевидно, А п.
Рассмотрим еще один пример.
Пример 4
По данному вектору  ÎV2 построить векторы (
ÎV2 построить векторы ( +
+  )
)  и (
и ( .
.  )
)  , если
, если  – симметрия относительно оси ОХ, а
– симметрия относительно оси ОХ, а  – поворот плоскости на 180о вокруг начала координат против часовой стрелки. Записать матрицы всех этих преобразований в каком-либо базисе.
– поворот плоскости на 180о вокруг начала координат против часовой стрелки. Записать матрицы всех этих преобразований в каком-либо базисе.
Пусть  – произвольный вектор плоскости, и (х, у) – его координаты в ортонормированном базисе
– произвольный вектор плоскости, и (х, у) – его координаты в ортонормированном базисе  . По условию (рисунок 1) имеем
. По условию (рисунок 1) имеем


 = (х, – у),
= (х, – у), 
 = (– х, – у).
= (– х, – у).
Обозначим C =  +
+  и
и 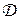 =
=  .
.  . Тогда
. Тогда
C  = (
= ( +
+  )
)  = (х, – у) + (– х, – у) = (0,–2 у),
= (х, – у) + (– х, – у) = (0,–2 у),
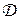
 = (
= ( .
.  )
)  =
=  (
(
 ) = ((– х), –(– у)) = (– х, у)
) = ((– х), –(– у)) = (– х, у)
|
Найдем матрицы этих преобразований в выбранном базисе  , для чего найдем координаты образов базисных векторов в этом базисе.
, для чего найдем координаты образов базисных векторов в этом базисе.
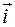 = (1, 0) Þ
= (1, 0) Þ  ,
,  , C
, C  = (
= ( +
+  )
)  = (0, 0),
= (0, 0),
 =(
=( .
.  )
)  = (–1, 0),
= (–1, 0),
 = (0, 1) Þ
= (0, 1) Þ 
 = (0, –1),
= (0, –1), 
 = (0, –1), C
= (0, –1), C  = (
= ( +
+  )
)  = (0, –2),
= (0, –2),
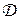
 = (
= ( .
.  )
)  = (0, 1).
= (0, 1).
Значит,
А =  , В =
, В = 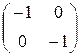 ,
,
С =  (сравните с А+В), D =
(сравните с А+В), D =  (сравните с АВ).
(сравните с АВ).
Заметим, что преобразование C =  +
+  – вырожденное.
– вырожденное.
Рассмотрим невырожденное преобразование  .
.
Определение 9
Преобразование  –1 , переводящее каждый вектор
–1 , переводящее каждый вектор  х в вектор х, называется обратным кпреобразованию
х в вектор х, называется обратным кпреобразованию  линейного пространства L.
линейного пространства L.
Можно показать, что справедливо равенство
 .
.  –1 =
–1 =  –1.
–1.  =
=  .
.
Если невырожденное преобразование  в некотором базисе задается невырожденной матрицей А, то обратное преобразование
в некотором базисе задается невырожденной матрицей А, то обратное преобразование  –1 задается в этом базисе матрицей А–1.
–1 задается в этом базисе матрицей А–1.
Преобразование, обладающее обратным, называется обратимым преобразованием.
Если обратимое преобразование  – линейное, то обратное преобразование
– линейное, то обратное преобразование  –1 также линейное, т.к., согласно определению 9,
–1 также линейное, т.к., согласно определению 9,
 –1(
–1( +
+  ) =
) =  –1(
–1( ) =
) =  =
=  –1(
–1( )+
)+  –1(
–1( ),
),
 –1(l
–1(l  ) =
) =  –1(
–1(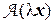 ) =
) =  =l
=l  –1(
–1( ).
).
Очевидно, тождественный оператор  является обратным самому себе.
является обратным самому себе.
Из полученных результатов следует, что операции над линейными преобразованиями обладают теми же свойствами, что и операции над матрицами, например, сложение коммутативно и ассоциативно:
 +
+  =
=  +
+  ,
,  +(
+( + C) = (
+ C) = ( +
+  ) + C;
) + C;
умножение ассоциативно, но не коммутативно:
C (
 ) = (C
) = (C  )
)  ,
, 
 ≠
≠ 
 .
.
Тождественное преобразование играет среди преобразований роль единицы, а нулевое – роль нуля.
Собственные векторы и собственные значения линейного преобразования
Пусть дана квадратная матрица порядка п

Составим для нее матрицу
(А – lЕ) = 
где l – произвольное число, а Е – единичная матрица. Матрица (А – lЕ) называется характеристической матрицей матрицы А, а уравнение
| А–lЕ | = 0 или  = 0
= 0
называется характеристическим уравнением матрицы А.
Очевидно, определитель | A – lЕ | является многочленом степени п относительно l. Этот многочлен также называют характеристическим многочленом матрицы А, корни этого многочлена называются характеристическими корнями (числами) матрицы А.
Можно доказать, что подобные матрицы обладают одинаковыми характеристическими многочленами, а, значит, и одинаковые характеристические корни.
Как мы знаем, между квадратными матрицами и линейными преобразованиями существует взаимно однозначное соответствие, причем матрицы, задающие линейное преобразование в разных базисах, подобны. Значит, хотя линейное преобразование в разных базисах задается различными матрицами, однако все эти матрицы имеют один и тот же набор характеристических корней. Поэтому характеристические корни матрицы преобразования называют характеристическими корнями самого преобразования. Рассмотрим одно из применений характеристических корней преобразования.
Определение 10
ПустьL n – линейное пространство,  :L n ® L n – линейное преобразование этого пространства. Ненулевой вектор и называется собственным вектором линейного преобразования
:L n ® L n – линейное преобразование этого пространства. Ненулевой вектор и называется собственным вектором линейного преобразования  , если он этим преобразованием переводится в вектор l и, т.е.
, если он этим преобразованием переводится в вектор l и, т.е.
 и = l и,
и = l и,
где l – некоторое действительное число. При этом l называется собственным числом или собственным значением линейного преобразования  , соответствующим собственному вектору и.
, соответствующим собственному вектору и.
Поскольку между линейными преобразованиями и матрицами в заданном базисе существует взаимно однозначное соответствие, то введенные понятия могут быть отнесены и к матрицам. Таким образом, если А – квадратная матрица (матрица линейного преобразования  в некотором базисе), Х – матрица-столбец координат вектора и ¹ 0 (в этом же базисе), то этот вектор называется собственным вектором матрицы А, а число l – собственным числом этой матрицы, если АХ = lХ.
в некотором базисе), Х – матрица-столбец координат вектора и ¹ 0 (в этом же базисе), то этот вектор называется собственным вектором матрицы А, а число l – собственным числом этой матрицы, если АХ = lХ.
Пусть и – собственный вектор линейного преобразования  , заданного в некотором базисе Б матрицей А, l – соответствующее этому вектору собственное значение, т.е.
, заданного в некотором базисе Б матрицей А, l – соответствующее этому вектору собственное значение, т.е.  и = l и, и ¹ 0. Обозначим Х =
и = l и, и ¹ 0. Обозначим Х =  – координатный столбец вектора и в базисе Б, тогда в матричном виде равенство
– координатный столбец вектора и в базисе Б, тогда в матричном виде равенство  и = l и запишется так
и = l и запишется так
АХ = lХ Þ АХ – lХ = О, (А – lЕ)Х = О.
Если А = 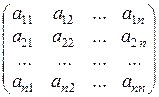 , то А – lЕ =
, то А – lЕ =  ,
,
и равенство (А – lЕ)Х = О равносильно системе линейных уравнений
 (*)
(*)
Поскольку Х – ненулевая матрица-столбец, то эта система имеет нетривиальное решение, что возможно лишь в том случае, когда определитель основной матрицы этой системы равен нулю, т.е. когда выполняется условие  .
.
Следовательно, собственные значения l преобразования  (или матрицы А) есть корни уравнения
(или матрицы А) есть корни уравнения  , т.е. действительные характеристические корни этого преобразования (матрицы).
, т.е. действительные характеристические корни этого преобразования (матрицы).
Наоборот, пусть l0 – характеристический корень преобразования  , т.е. l0 является корнем характеристического многочлена
, т.е. l0 является корнем характеристического многочлена  . Тогда при l = l0 определитель системы (*) равен нулю, следовательно, система имеет нетривиальное решение. Поскольку система (*) равносильна матричному уравнению
. Тогда при l = l0 определитель системы (*) равен нулю, следовательно, система имеет нетривиальное решение. Поскольку система (*) равносильна матричному уравнению  , или
, или  , то решение системы есть столбец Х=
, то решение системы есть столбец Х=  , который можно рассматривать как координатный столбец вектора и, удовлетворяющего равенству
, который можно рассматривать как координатный столбец вектора и, удовлетворяющего равенству  и = l0 и, т.е. собственного вектора преобразования
и = l0 и, т.е. собственного вектора преобразования  , соответствующего собственному значению l0.
, соответствующего собственному значению l0.
Таким образом мы доказали, что действительные характеристические корни линейного преобразования, если они существуют, и только они являются собственными значениями этого преобразования.
Собственное значение называется т -кратным, если оно является т -кратным корнем характеристического уравнения. Если собственное значение – простой корень характеристического уравнения, то его называют простым собственным значением.
Из вышесказанного вытекает а лгоритм нахождения собственных значений и собственных векторов преобразования  :
:
1. Выбирают в заданном линейном пространстве произвольный базис.
2. Находят матрицу А преобразования  в этом базисе.
в этом базисе.
3. Находят характеристические числа преобразования  , решив уравнение
, решив уравнение
 , т.е.
, т.е. 
и выбирают из них действительные, которые и являются собственными значениями. Если нет действительных характеристических корней, то нет ни собственных значений, ни собственных векторов.
4. Составляют систему 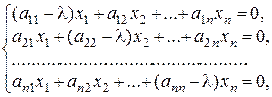 (7.1)
(7.1)
и, полагая l равным одному из найденных собственных значений l i, находят ненулевое решение Х i = 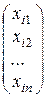 этой системы. Полученный вектор и i = Х i =
этой системы. Полученный вектор и i = Х i = 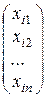 и есть собственный вектор, соответствующий взятому собственному значению l i.
и есть собственный вектор, соответствующий взятому собственному значению l i.
5. Пункт 4 этого алгоритма повторяют для каждого собственного значения.
Обратите внимание, что поскольку для каждого собственного значения l i система (7. 1) имеет множество решений, то для данного преобразования существует бесконечное число собственных векторов, соответствующих собственному числу l i.
Пример 6
Найти собственные векторы преобразования  , заданного матрицей А =
, заданного матрицей А =  .
.
Решение
Пункты 1 и 2 указанного алгоритма уже выполнены. Рассмотрим сразу третий пункт. Составим характеристическое уравнение  и найдем его корни:
и найдем его корни:
 =
=  = – (1–l)(1+l) –3 = – (1–l2) – 3 = l2 – 4,
= – (1–l)(1+l) –3 = – (1–l2) – 3 = l2 – 4,
l2 – 4 = 0 Þ l1 = 2, l2 = –2.
Это действительные числа, значит, они являются собственными значениями.
Составим систему вида (7.1):  Найдем решения этой системы для каждого из полученных собственных значений.
Найдем решения этой системы для каждого из полученных собственных значений.
При  получим
получим 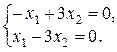 Ранг этой системы, очевидно, равен 1, значит, система равносильна одному уравнению
Ранг этой системы, очевидно, равен 1, значит, система равносильна одному уравнению 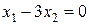 , решая которое, находим х 1 = 3 х 2. Положим х 2 = t, получим x 1 = 3 t, тогда собственный вектор и 1 = (3 t, t) соответствует собственному значению
, решая которое, находим х 1 = 3 х 2. Положим х 2 = t, получим x 1 = 3 t, тогда собственный вектор и 1 = (3 t, t) соответствует собственному значению  .
.
При  получим систему
получим систему  ранг которой также равен 1, поэтому она равносильна уравнению х 1 + х 2 = 0, откуда х 1 = – х 2.При
ранг которой также равен 1, поэтому она равносильна уравнению х 1 + х 2 = 0, откуда х 1 = – х 2.При 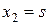 , получим
, получим  , откуда имеем собственный вектор и 2 = (– s, s), соответствующий собственному значению l1 = – 2.
, откуда имеем собственный вектор и 2 = (– s, s), соответствующий собственному значению l1 = – 2.
Таким образом, имеем семейство собственных векторов и 1 = (3 t, t), соответствующих собственному числу l1 = 2 и семейство собственных векторов и 2 = (– s, s), соответствующих собственному числу l1 = – 2.






