Содержание лекции: Отображения пространств. Линейные отображения, линейные преобразования линейных пространств, матрица преобразования. Характеристические корни матрицы преобразования. Собственные числа и собственные векторы линейных преобразований.
Операции над линейными преобразованиями. Свойства операций.
Свойства собственных значений и собственных векторов. Ортогональные и симметрические преобразования. Приведение симметрической матрицы к диагональному виду.
Отображения, линейные отображения. Примеры.
Основополагающее понятие математического анализа – понятие функции – определяется как соответствие между числовыми множествами Х и У: каждому значению х ÎХ по определенному закону ставится в соответствие единственное значение у ÎУ. Очевидно, в этом определении природа множеств Х и У не играет существенной роли. Это позволяет обобщить понятие функции на случай произвольных множеств. В этом случае вместо термина «функция» употребляется термин «отображение» или «оператор». Здесь мы рассмотрим понятие отображения множеств, являющихся линейными пространствами.
Определение 1
Пусть L и К линейные пространства размерности п и т соответственно. Говорят, что задано отображение 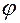 линейного пространства L в пространство К, или оператор, переводящий L в К, если задан закон, по которому каждому вектору х ÎL поставлен в соответствие единственный вектор у ÎК. Обозначают
линейного пространства L в пространство К, или оператор, переводящий L в К, если задан закон, по которому каждому вектору х ÎL поставлен в соответствие единственный вектор у ÎК. Обозначают
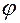 : L ® К, или L
: L ® К, или L 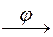 К.
К.
При этом вектор у называют образом вектора х при отображении  и обозначают
и обозначают 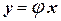 , а вектор х называют прообразом вектора у. Совокупность всех прообразов (множество L) называют областью определения отображения
, а вектор х называют прообразом вектора у. Совокупность всех прообразов (множество L) называют областью определения отображения  , а совокупность образов (множество К или его подмножество) называют областью значений этого отображения. Пространство К, в частности, может совпадать с пространством L.
, а совокупность образов (множество К или его подмножество) называют областью значений этого отображения. Пространство К, в частности, может совпадать с пространством L.
Рассмотрим примеры отображений.
I. Отображение  : М2 ® М1´2 такое, что для вектора х =
: М2 ® М1´2 такое, что для вектора х = 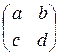 ÎМ2 образ имеет вид у =
ÎМ2 образ имеет вид у = 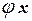 =
= 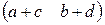 ÎМ1´2.
ÎМ1´2.
II. Оператор  : V3® R такой, что "` х Î V3
: V3® R такой, что "` х Î V3 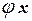 =
= 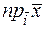 .
.
III. Отображение  : R2®R2 такое, что вектору х = [ х 1, х 2]ÎR2 ставится в соответствие вектор у =
: R2®R2 такое, что вектору х = [ х 1, х 2]ÎR2 ставится в соответствие вектор у = 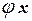 =
= 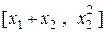 .
.
IV. Отображение  :L ® L, при котором образом каждого вектора пространства L является сам этот вектор. Такой отображение называется тождественным или единичным и обозначается
:L ® L, при котором образом каждого вектора пространства L является сам этот вектор. Такой отображение называется тождественным или единичным и обозначается 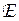 . Таким образом, " х Î L
. Таким образом, " х Î L 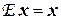 .
.
V. Оператор  : L ® К такой, что каждому вектору из L ставит в соответствие нулевой вектор из К. Этот оператор называется нулевым оператором и обозначаетсяO. Таким образом, " х Î L O х = 0, где 0 – нулевой вектор пространства К.
: L ® К такой, что каждому вектору из L ставит в соответствие нулевой вектор из К. Этот оператор называется нулевым оператором и обозначаетсяO. Таким образом, " х Î L O х = 0, где 0 – нулевой вектор пространства К.
Определение 2
Оператор (отображение)  : L ® К называется линейным, если для любых х 1, х 2ÎL и любого aÎR выполняются условия линейности:
: L ® К называется линейным, если для любых х 1, х 2ÎL и любого aÎR выполняются условия линейности:
1)  (х 1+ х 2) =
(х 1+ х 2) =  х 1 +
х 1 +  х 2, 2)
х 2, 2)  (a х 1) = a
(a х 1) = a  х 1.
х 1.
Чтобы выяснить, является ли заданный оператор линейным, необходимо проверить выполнение обоих условий линейности.
Пример 1
Проверить линейность оператора:
 : V3® R, если " `а Î V3
: V3® R, если " `а Î V3 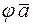 =
= 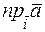 .
.
Пусть `а 1, `а 2 – произвольные векторы пространства V3, заданные в базисе 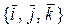 своими координатами: `а 1=
своими координатами: `а 1= 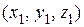 , `а 2 =
, `а 2 = 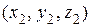 .
.
Тогда
`а 1 + `а 2 = 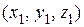 +
+ 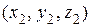 =
= 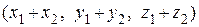 ,
,
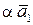 = a
= a 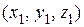 =
= 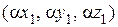 .
.
Отсюда 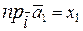 ,
, 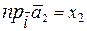 ,
, 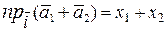 ,
, 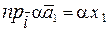 .
.
Проверим выполнение условий линейности для оператора  :
:
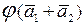 =
= 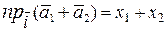 =
= 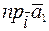 +
+ 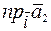 =
= 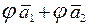 ,
,
следовательно, первое условие линейности выполнено;
 (
(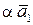 ) =
) = 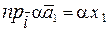 = a
= a 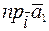 = a
= a 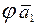 ,
,
т.е. второе условие линейности тоже выполнено. Значит, рассмотренный оператор – линейный.
Пример 2
Проверить линейность оператора  : R2®R2, если " х = [ х 1, х 2]ÎR2
: R2®R2, если " х = [ х 1, х 2]ÎR2 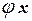 =
= 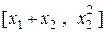 .
.
Пусть х = [ х 1, х 2], у = [ y 1, y 2] – произвольные векторы пространства R2. Тогда 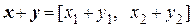 ,
, 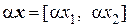 .
.
Проверим выполнение условий линейности для заданного оператора.
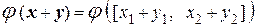 =
= 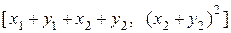 ,
,
 х +
х +  у =
у = 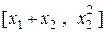 +
+ 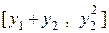 =
= 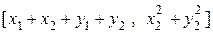 .
.
Первые компоненты векторов  и
и  х +
х +  у, очевидно, совпадают. Но
у, очевидно, совпадают. Но
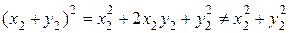 ,
,
т.е. вторые компоненты этих векторов не совпадают, поэтому
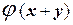 ≠
≠  х +
х +  у.
у.
Следовательно, заданный оператор не является линейным.
Из определения линейного оператора следуют такие свойства:
1. При любом линейном отображении образом нулевого вектора является нулевой вектор, т.е. если оператор  – линейный, то
– линейный, то
 0 L= 0 K.
0 L= 0 K.
2. При любом линейном отображении образом вектора, противоположного для данного вектора х, является вектор, противоположный для образа вектора х, т.е.  (–а) = –
(–а) = –  а.
а.
Линейные преобразования. Матрица линейного преобразования
Наиболее часто в линейной алгебре приходится иметь дело с операторами, отображающими заданное линейное пространство в это же линейное пространство. Такие отображения называют преобразованиями линейных пространств.
Определение 3.
Оператор  , действующий из L в L, т.е.
, действующий из L в L, т.е.  : L ® L, называется преобразованием линейного пространства L.
: L ® L, называется преобразованием линейного пространства L.
Это означает, что каждому вектору х из L по закону  ставится в соответствие вполне определенный вектор у из этого же пространства L.
ставится в соответствие вполне определенный вектор у из этого же пространства L.
Преобразования линейных пространств будем обозначать буквами  ,
, 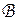 , C,
, C, 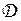 , и т.д.
, и т.д.
Самым простым, и в то же время очень важным видом преобразований являются линейные преобразования. Поэтому дальнейшее изложение будет посвящено именно линейным преобразованиям линейных пространств.
Линейные преобразования можно записывать в координатной форме, т.е. для них существует единое правило нахождения координат образа по координатам прообраза.
Действительно, пусть 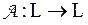 – линейное преобразование линейного пространства L, х Î L – произвольный вектор, у =
– линейное преобразование линейного пространства L, х Î L – произвольный вектор, у =  – его образ, у ÎL. Установим связь между координатами векторов х и у. Поскольку координаты вектора зависят от базиса, то зададим некоторый базис Б:{ а 1, а 2, …, а п } пространства L. Пусть
– его образ, у ÎL. Установим связь между координатами векторов х и у. Поскольку координаты вектора зависят от базиса, то зададим некоторый базис Б:{ а 1, а 2, …, а п } пространства L. Пусть
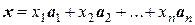 ,
,
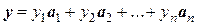 .
.
Поскольку 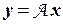 , то
, то 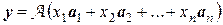 . В силу линейности преобразования
. В силу линейности преобразования  имеем
имеем
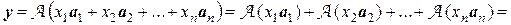
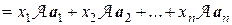 .
.
Векторы 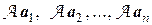 – образы векторов базиса Б – являются элементами пространства L, и значит, могут быть разложены по базису Б:
– образы векторов базиса Б – являются элементами пространства L, и значит, могут быть разложены по базису Б:
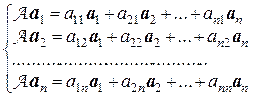
Тогда для вектора у получим
у 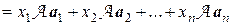 =
= 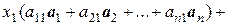
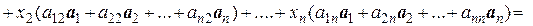
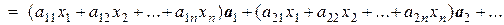
 .
.
Отсюда, в силу единственности разложения вектора 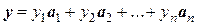 по базису, имеем
по базису, имеем
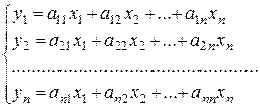 (1).
(1).
Формулы (1) определяют правило нахождения координат образа у через координаты его прообраза х при линейном преобразовании. Если координатные столбцы векторов х и у обозначить соответственно
Х =  и У =
и У = 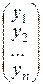
то систему (1) можно записать в матричном виде У =А.Х, (2)
где А = 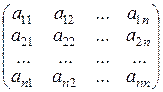 – квадратная матрица порядка п, i -й столбец которой составлен из координат вектора
– квадратная матрица порядка п, i -й столбец которой составлен из координат вектора 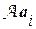 в выбранном базисе Б. Очевидно, А есть матрица системы векторов
в выбранном базисе Б. Очевидно, А есть матрица системы векторов 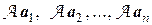 в базисе Б.
в базисе Б.
Таким образом, при фиксированном базисе любое линейное преобразование можно представить и притом единственным образом в матричной форме (2), или координатной форме (1)
Отсюда следует, что
· каждому линейному преобразованию в заданном базисе соответствует квадратная матрица, позволяющая осуществлять это преобразование посредством чисел – координат векторов и элементов данной матрицы;
· наоборот, любая квадратная матрица определяет в линейном пространстве L некоторое линейное преобразование, при котором координаты образа находятся по координатам прообраза с помощью системы (1).
Итак, мы имеем взаимно однозначное соответствие между множеством линейных преобразований линейного пространства L n и множеством квадратных матриц порядка п. Это соответствие, конечно, зависит от выбора базиса.
Определение 4.
Матрицей линейного преобразования  в базисе Б называется матрица системы образов векторов базиса Бпри этом преобразовании.
в базисе Б называется матрица системы образов векторов базиса Бпри этом преобразовании.
Чтобы найти матрицу линейного преобразования  , нужно:
, нужно:
1) выбрать базис рассматриваемого пространства;
2) найти образы базисных векторов при преобразовании  ;
;
3) разложить полученные образы по выбранному базису;
4) составить матрицу, расположив в её столбцах координаты образов базисных векторов. Это и будет искомая матрица преобразования  .
.
Пример 3
Найти матрицу линейного преобразования:
а) тождественного;
б) нулевого;
в)  : R2®R2, такого, что " х = [ х 1, х 2]ÎR2
: R2®R2, такого, что " х = [ х 1, х 2]ÎR2  =
= 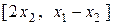 *).
*).
а) Пусть  : L ® L такой, что " х Î L
: L ® L такой, что " х Î L 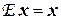 . Рассмотрим какой-либо базис Б:{ а 1, а 2, …, а п } пространства L. Тогда
. Рассмотрим какой-либо базис Б:{ а 1, а 2, …, а п } пространства L. Тогда
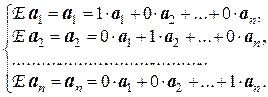
Отсюда получим матрицу преобразования 
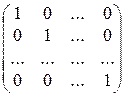 = Е,
= Е,
т.е. матрицей тождественного преобразования является единичная матрица.
б) Рассмотрим нулевое преобразование  : L ® L, такое, что
: L ® L, такое, что  х = 0. Выбрав произвольный базис Б:{ а 1, а 2, …, а п } пространства L, получим
х = 0. Выбрав произвольный базис Б:{ а 1, а 2, …, а п } пространства L, получим
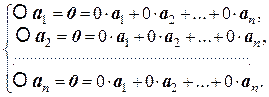
Отсюда получаем матрицу преобразования  :
:
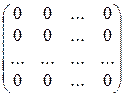 .
.
Следовательно, матрицей нулевого преобразования является нулевая матрица.
в) Для преобразования  :R2®R2, переводящего вектор х = [ х 1, х 2] в вектор
:R2®R2, переводящего вектор х = [ х 1, х 2] в вектор  =
= 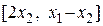 , найдем матрицу в каноническом базисе Бк:{ е 1= [1, 0], е 2 = [0, 1]}. Имеем
, найдем матрицу в каноническом базисе Бк:{ е 1= [1, 0], е 2 = [0, 1]}. Имеем
 е 1= [2.0, 1– 0] = [0, 1] = 0 е 1+ 1 е 2,
е 1= [2.0, 1– 0] = [0, 1] = 0 е 1+ 1 е 2,
 е 2 = [2.1, 0 – 1] = [2, –1] = 2 е 1+ (–1) е 2.
е 2 = [2.1, 0 – 1] = [2, –1] = 2 е 1+ (–1) е 2.
Тогда матрица этого преобразования А = 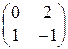 .
.
Поскольку матрица линейного преобразования зависит от базиса, то возникает вопрос: как связаны между собой матрицы одного и того же преобразования в разных базисах? Справедлива следующая теорема.
Теорему 1
Если А – матрица линейного преобразования  в базисе Б1, а А¢ – матрица этого же преобразования в базисе Б2, то А¢ = Т–1.А.Т, где Т – матрица перехода от базиса Б1 к базису Б2.
в базисе Б1, а А¢ – матрица этого же преобразования в базисе Б2, то А¢ = Т–1.А.Т, где Т – матрица перехода от базиса Б1 к базису Б2.
Определение 5
Матрицы А и В называются подобными, если существует невырожденная матрица S такая, что В = S–1.А.S.
Согласно этому определению и теореме 6.2, матрицыодного и того же преобразования в разных базисах подобны.
Итак, мы установили соответствие между всеми линейными преобразованиями пространства L п и всеми квадратными матрицами порядка п. Это соответствие зависит от базиса, причем матрицы, задающие линейное преобразование в разных базисах, подобны между собой.






