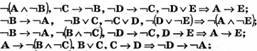Логическая корректность рассуждения 1 страница

Рассуждением называется логическая форма теоретического познания, в результате которой из множества исходных суждений (посылок) по логи­ческим правилам выводится новое суждение (за­ключение). По структуре рассуждение, таким обра­зом, представляет собой последовательность суж­дений, состоящую из посылок и заключения, объединенных отношением логического следования. По типу логического следования различают дедук­тивные и индуктивные рассуждения.

Дедуктивным называется рассуждение, в кото­ром заключение следует из посылок с логической необходимостью, то есть для дедуктивных рассужде­ний имеется разрешающая процедура, позволяющая в конечное число шагов установить, является ли заключение логическим следствием из данных по­сылок или нет. Пример дедуктивного рассуждения: «Если я поступаю на дневное отделение института,

значит мне не более 35 лет. Мне 40 лет. Следователь­но, я не поступаю на дневное отделение института».

Индуктивным называется рассуждение, в кото­ром заключение следует из посылок с вероятностью, поэтому индуктивные рассуждения называют также вероятностными или правдоподобными рассуждени­ями. Пример индуктивного рассуждения: «Населе­ние Ростова-на-Дону превышает 500 тысяч человек. Население Курска превышает 500 тысяч. Население Новосибирска превышает 500 тысяч. Следователь­но, все областные центры России имеют население свыше 500 тысяч человек». Ясно, что заключение этого рассуждения следует из данных посылок толь­ко с долей вероятности и, в принципе, не является необходимым. Вполне возможно, что в России име­ется областной центр с населением, не превышаю­щим 500 тысяч человек.

Рассуждение считается логически корректным тогда и только тогда, когда заключение в нем логи­чески следует из заданных посылок. Поэтому про­блема контроля логической корректности рас­суждений сводится к решению вопроса, имеется ли отношение логического следствия между посылка­ми и заключением рассуждения или нет. Понятие логического следствия является центральным в тео­рии рассуждений. Определение этого понятия вве­дем, используя условия истинности суждений, следу­ющим образом.

Заключение в рассуждении логически следует из заданных посылок, если и только если заключение истинно в каждой такой логически возможной ситу­ации, в которой истинны посылки. Короче говоря, заключение следует из посылок, если оно истинно при условии истинности посылок. И наоборот, заключение не следует в рассуждении из заданных посылок лишь в одном случае: если имеется, по крайней мере, одна логически возможная ситуация, в которой посылки истинны, а заключение оказа­лось ложным.

Проиллюстрируем введенные определения на примерах конкретных дедуктивных рассуждений. Требуется установить, являются ли следующие рас­суждения логически корректными:

1. Если я поступил в университет, значит, я окон­чил среднюю школу. Я поступил в университет. Сле­довательно, я окончил среднюю школу. Структура рассуждения имеет вид (А—»В), А=>В.

2. Если я поступил в университет, значит, я окон­чил среднюю школу. Я окончил среднюю школу. Следовательно, я поступил в университет. Структура рассуждения имеет вид (А—>В), В=>А.

3. Если я окончил среднюю школу, значит, я по­ступил в университет. Я окончил среднюю школу. Следовательно, я поступил в университет. Структура рассуждения имеет вид (В—»А), В=>А.

Построим для каждой структуры рассуждений таблицы истинности.

(А	-»в]	1, в =>	А	(в	-а),	в =»	А

(а ->. в), а ^ в ill

10 1

В соответствии с введенными определениями по­нятий логической корректности рассуждения и логического следования заключения из посылок по таблицам истинности установим отношения сле­дования.

В рассуждении №1 условие истинности обеих посылок выполняется лишь для первой строки, то есть для первой логически возможной ситуации. При этом заключение оказывается также истин­ным. По определению логического следствия это означает, что заключение данного рассуждения ло­гически следует из посылок. А по определению логической корректности, в свою очередь, следует признать, что рассуждение №1 является логически корректным.

В рассуждении №2 условие истинности обеих посылок выполняется для первой и третьей логичес­ки возможных ситуаций. В первой строке заключе­ние также истинно, но в третьей оно оказывается ложным. Это нарушает определение логического след­ствия, поэтому рассуждение №2 не является логичес­ки корректным.

В рассуждении №3 условие истинности обеих посылок выполняется опять же лишь для первой логически возможной ситуации. Заключение при этом также оказывается истинным. Значит, заклю­чение логически следует из посылок, а,рассуждение №3 в целом является логически корректным. Здесь обычно появляются вопросы и недоумения: ведь ясно, что первая посылка рассуждения №3 содер­жательно ложна. Поэтому принять данное рассуж­дение — значит войти в противоречие с собствен­ными содержательными интуициями. Действитель­но, рассуждение №3 противоинтуитивно и принять его нельзя, но не по логическим основаниям. С ло­гической точки зрения оно корректно, так как вы­полняет определение логического следствия. С точ­ки же зрения содержательного анализа оно не на­дежно, так как одна из его посылок ложна. Однако

установление истинности посылок рассуждения не является предметом логического исследования. В логической теории рассуждений проверяется лишь факт истинности заключения, если допустить, что посылки при этом истинны. Поэтому следует раз­личать понятия логической корректности и надеж­ности рассуждения.

Рассуждение называется надежным, если и только если оно логически корректно и его посыл­ки истинны.

Логическую корректность рассуждения можно проверить методом сокращенных истинностных таб­лиц, размышляя от противного. Допустим, что рас­суждение не корректно, то есть в нем заключение не следует из посылок. По определению логического следствия допущение означает, что существует по крайней мере одна логически возможная ситуация, в которой посылки истинны, а заключение ложно. Если при сделанном допущении можно реконструи­ровать такую ситуацию без противоречия в распре­делении истинностных значений, значит, заключение не следует из посылок, а рассуждение в целом не корректно. Если же допущение влечет противоречие, значит, оно сделано неверно, то есть заключение не может быть ложным при условии истинности посы­лок. Таким образом, заключение истинно при истин­ности посылок и логически следует из них, а рас­суждение в целом является логически корректным. Объясним метод на примере.

Пример. Проверьте логическую корректность сле­дующего рассуждения: «Неправда, что я хорошо сдам экзамен по логике, но на меня не обратят внимание девушки (юноши). Если я не буду заниматься спортом, то на меня перестанут обращать внимание девушки (юноши). Либо я выиграю ближайшее соревнование, либо вообще брошу спорт. Следовательно, если я хоро­шо сдам экзамен по логике, то и выиграю ближай­шее спортивное соревнование».

Решение. Допустим, что данное рассуждение не корректно и заключение в нем не следует из посы­лок, то есть заключение может быть ложным при условии истинности посылок. Для сделанного допу­щения построим таблицу истинности, предварительно представив рассуждение в формулах языка класси­ческой логики высказываний.

а л -,в), (~,с -> -,в), (d v -пС) => (а -> в)
~,(а л -,в)], 1	_,с -»-,в	, 1	D v -,С] => 0 [А -* d] Допущение
^Ал-л)1. 1	_,с ^-,в	, 1	d v -,с] => 1 [а], о \d] \->
Ал-JS], 1	_,с -» -,в	, 1	d v -,cl => 1 [а], о [d! [-,
-,Bl, 1	-,с-*-,в	, 1	D v -,С] => 0 [d] [л
-&], 1

t

-iC -> -.В		-,с] [v
-В], 1
в], о [в] h

Сокращенная запись решения имеет следующий вид:

-{а л -,в), (-,с -»-в), (d v -л) => (а -» d)

11001 10 110 0110 100

В процессе построения таблицы истинности при­шли к противоречию. Следовательно, допущение сде­лано неверно, то есть заключение рассуждения не может быть ложным при условии истинности по­сылок ни в одной логически возможной ситуации. Значит, заключение истинно при условии истинности посылок в каждой логически возможной ситуа­ции. По определению понятия логического след­ствия это означает, что заключение логически сле­дует из заданных посылок. В свою очередь, по опре­делению понятия логической корректности это влечет логическую корректность рассматриваемого рассуждения.

Упражнения

4.1. Проверьте логическую корректность следую­щих рассуждений, предварительно предста­вив их в формулах языка логики высказыва­ний.

1. Если я отлично сдам вступительные экза­мены, то поступлю в институт. Я не поступил в институт. Следовательно, я не сдал отлично вступительные экзамены.

2. Если я не поступил в университет, значит, плохо сдал вступительные экзамены. Я по­ступил в университет. Следовательно, я хоро­шо сдал вступительные экзамены.

3. Я сдам экзамен по логике, если и только если научусь решать задачи и мне немного повезет. Значит, если я так и не научусь ре­шать задачи или мне не повезет, то я прова­лю экзамен.

4. Либо я не пойду на дискотеку, либо лягу спать поздно. Невозможно лечь спать поздно, а встать рано. Если я не встану утром рано, то опоздаю на занятия по логике. Следова­тельно, я не пойду на дискотеку или опоздаю на занятия по логике.

4.2. Проверьте логическую корректность следу­ющих рассуждений, подобрав подходящий пример перевода формул на естественный язык:

1. -iA->B,-iA->-iB=» A.

2. A-»C,B->C,AvB=>C.

3. ^AvB,^(BA^C),-iD->-iC,Ev-iD=>-iE->-iA.

4. -iB -» -iА, С v -iB, -i(-iD а С), D -> E => -(А д -iE).

5. -i

4.3. В Древней Греции судебный спор часто ре­шался по логическим основаниям. Чтобы снять обвинение, достаточно было доказать свою невиновность, независимо от того, совер­шил ли в действительности доказывающий преступление или нет. Однажды, устав от до­проса трех обвиняемых в краже и запутав­шись в противоречивых показаниях этих хит­рецов, судья решил положиться на волю Бо­гов и Логики, что, впрочем, одно и то же. «Я знаю, что кражу совершили двое из вас, но не знаю, кто именно. Каждому я скажу, что думаю, или считаю нужным сказать от­носительно виновности двух других, но не о его виновности. О своем мнении относитель­но вины каждого из вас я сообщу двум дру­гим одно и то же. Кто первый угадает, что я сказал о нем, тот будет признан невиновным, а остальные двое — осуждены». С этими сло­вами судья прошептал на ухо каждому из трех: «Думаю, что они оба не виновны». Не­много подумав, один из обвиняемых все же угадал: «Вы сообщили двум другим, что я не

виновен».

Воспроизведите рассуждения счастливца.

4.2. Дедуктивная система натурального вывода

Существуют различные, но эквивалентные меж­ду собой формы построения логической теории рас­суждения. Наиболее удобной из них является сис­тема натурального вывода, содержащая только правила логического перехода или вывода от од­них формул языка классической логики высказы­ваний к другим. Само название указывает на то, что выводы в данной системе близки к естествен­ным формам практического рассуждения. Это зна­чительно облегчает проверку логической кор­ректности рассуждений и поиск методов такой проверки. Кроме того, система натурального выво­да более удобна в методологии гуманитарных наук — юриспруденции, эстетики, этики, язык ко­торых содержит нормативные и оценочные сужде­ния, не имеющие истинностной интерпретации. Понятие логического следствия, определенное в терминах истинности, — заключение логически следует из посылок, если оно истинно при условии истинности посылок — не «работает» в языке с нормативными и оценочными суждениями. Дей­ствительно, в каком смысле это определение при­менимо для проверки корректности, скажем, рассуж­дения: «Если хочешь быть опрятным, должен брить­ся по утрам. Хочу быть опрятным. Следовательно,

должен бриться утром»? Ведь заключение рассужде­ния не является ни истинным, ни ложным, а пред­ставляет собой норму.

В системе натурального вывода понятие логическо­го следствия определяется без использования понятия истинности. Заключение в рассуждении логически сле­дует из посылок, если и только если оно выводимо из заданных посылок по определенным для системы ло­гическим правилам. Выводом в натуральной системе будем называть последовательность формул языка клас­сической логики высказываний, каждая из которых является либо посылкой, либо формулой, полученной из предшествующих в последовательности формул по оп­ределенным в системе логическим правилам. После­дняя формула последовательности вывода называется выводимой формулой или заключением вывода.

Логические правила вывода контролируют две формы оперирования логическими связками языка в исследовании информации. В процессе анализа ин­формация расчленяется на составные части удалени­ем из нее логических связок; в процессе синтеза, на­оборот, разрозненная информация объединяется в це­лое введением в нее соединяющих логических связок. Итак, различают правила введения и удаления. Основные правила логического вывода:

[УО] -т-iA => А [ВО] А => В, А. -» -,В

-iA

[УК] А л В => А; АлВ => В [вк]А,В=>АлВ
[УД] А => С, В => С, A vB => С [ВД]Л => A vB;B => A vB

[уи] А -> В, А => В [ВИ] Г, А^ => В, где Г - формулы

Г => А —» В, вывода

Правило введения отрицания [ВО] называют так­же правилом сведения к противоречию — или пра­вилом рассуждения от противного. Оно утверждает, что для обоснования выводимости некоторой форму­лы, например —iA, достаточно ввести в вывод в каче­стве дополнительной посылки косвенного допущения (п.к.д.) ее отрицание, то есть А, и показать, что сделан­ное допущение влечет противоречие: В и -iB.

	А -» В, -JB	=> —,Л Правило «модус толленс»	[МТ]
1.	А -> В	посылка
2.	~,В	посылка
3.	-,-,А	п.к.д.
4.	А	(3), УО
5.	В	(1,4), УИ
		(1), (5) — противоречие.

Правило удаления дизъюнкции [УД] называ­ют также правилом рассуждения по случаям. Оно утверждает, что для обоснования выводимости фор­мулы иэ посылок, содержащих дизъюнкцию, т.е. AvB=>C, достаточно доказать два случая: когда в качестве посылки используется один дизъюнктор, т.е. А=>С, и когда посылкой является другой дизъюнк­тор, т.е. В=»С.

A v В, -.В => А Правило «модус толлендо поненс» [МТП]
1.	1. А 2. -,1 3. -,j (1>, (3)	посылка 3 посылка V п.к.д. — противоречие.	2. 1. В 2. -,В 3. ^А (1), (2) —	посылка посылка П.К.Д. противоречие.

Правило удаления импликации [УИ] называют также правилом «модус поненс» [МП].

Правило введения импликации [ВИ] называют также принципом дедукции [ПД]. Оно утверждает, что для обоснования выводимости формулы, имею­щей импликативную структуру, т.е. Г=>А-»В, дос­таточно построить вывод ее консеквента, в котором антецедент импликативной формулы фигурирует в качестве посылки, т.е. Г, А

А-»В,В-»С=>А-»С Правило силлогизма [ПС]

А -> В, В -> С, А => С по правилу [ВИ] [ПД]

1. А -» В посылка

2. В -» С посылка

3. А посылка

4. В (1,3), МП [УИ]

5. С (2,4), МП [УИ]

В системе натурального вывода различают Основ­ные и производные логические правила. Производ­ные правила выводимы из основных и после своего логического обоснования могут использоваться в последующих рассуждениях. Таким образом, правила МТ, МТП и ПС являются производными в системе натурального вывода.

-.(а л -ж), в -» с => -,с -> -iA
-i(A л -,В); В -» С, -,С => -,А		[ПД]
1. -(А л -,В) посылка	5. А	(4), УО
2. В -» С посылка	6. -iB	(2, 3), МТ
3. -,С посылка	7. Ал-,	В (5, 6), ВК
4. -т-,А п.к.д.	(Т), (7) -	противоречие.

В натуральной системе различают прямой и кос­венный вывод. Прямым выводом называется переход по логическим правилам от данной, уже полученной в выводе формулы к выводимой, то есть результирую­щей формуле. Косвенным выводом называется пере­ход от данного вывода к результирующему выводу по логическим правилам. Таким образом, основные ло­гические правила ВО, УД и ВИ являются правилами косвенного вывода. С другой стороны, построенный выше вывод А—»В, В—> С, А => С является прямым, так как в нем осуществляется переход от формулы к фор­муле, но не от вывода к выводу. Построение прямого вывода обычно представляет эвристические трудно­сти, — да мы так и не рассуждаем, — поэтому кос­венный вывод принципиально облегчает нахождение метода нормализации вывода.

А -» -,((В л -,c)v Т)} С -> Е => В -»• (А -> е)
А -» -,((В л -,С) v d) С -» Е, В => А -» Е	[ПД]
А -> -4(в л -,c)v D\ С -» Е, В, А => Е	[ПД]
1. А -> -н((в /	\-,C)vD) посылка 6. -,((В A-,C)vD) (1, 4), МП
2. С-»Е	посылка 7. -iC (2, 5), МТ
3. В	посылка 8. В л -iC (3, 7), ВК
4. А	посылка 9. (BA-,c)vD (8), ВД
5. -,Е	п.к.д. (6), (9) — противоречие.

Укажите применение производного и косвенного правил вывода.

Упражнения

4.4. Дайте необходимые логические обоснования для каждого шага следующего вывода:

•-А v В, -,С -> -,В, -,((С л -nD) v е) =* -,((А л -Л>) v е) 1- -,А, -,С -» -,В, -,((С л -iD) v е) =» -,((А л -,О) v е)

п- в, -,с -> -,в, Ц(с л -,d) v е) => -,((а л ^d) v e)

I. 1. -А.

2. -пС -» -.В

3. -,((с л -,»)v е)

4. •-,-i((aa-,d)ve)

5. (aa-,d)ve

6.1. Ал-^D 6.2. Е
7.1. А 7.2. (CA^D)vE.
(?) — противоречие (?) — противоречие
И. 1. В

2. -,С -> ~,В

3. -,((ca-d)ve)

4. -,-,((aa-,d)ve)

5. (aa-,d)ve

6.1. Ал^В 6.2. Е

7.1. ^D 7.2. (CA-iD)vE

8.1. С (?) — противоречие

9.1. Сл-0>

10.1. (CA-,D)vE (?)— противоречие

4.5. Установите логическую корректность следу­ющих рассуждений методом натурального вывода. Подберите подходящие примеры пе­ревода логических структур рассуждений на естественный язык.