Етапи розв'язання задач на компю'ютерi
Незважаючи на рiзноманiтнiсть програм,у самому процесi iх створення можно знайти щось узагальнююче. Розглянемо основнi етапи пiдготовки та розв'язання задач за допомогою комп'ютера.
Постановка задачі. Розв’язання будь-якої задачі починається а її постановки, викладеної мовою чітко визначених математичних понять. При цьому слід добре уявити суть поставленої задачі, необхідні початкові дані та інформацію, що вважається результатами розв’язання.
Побудова математичної моделі. Не завжди умова сформульованої задачі містить у собі готову математичну формулу, яку можна застосувати для розробки алгоритму задачі, і не завжди розв’язок задачі вдається одержати в явному вигляді, що пов’язує вихідні дані та результат. Для цього створюється інформаційна математична модель об’єкта, і чим достовірніше вона відображає реальні сторони об’єкта, тим точніші одержані результати. Тут особливо важлива однотипність методів розв’язання задач.
Розробка алгоритму. Створення алгоритму, тобто послідовності вказівок для розв’язання задачі, відбувається на основі побудованої математичної моделі.
З метою знаходження способу розв’язання поставленої задачі можуть бути застосовані вже відомі методи, проведена їх оцінка, аналіз, відбір або розроблені нові методи. При створенні складних алгоритмів застосовується метод покрокової розробки, сутність якого полягає в тому, що алгоритм розробляється «зверху донизу». Такий підхід дозволяє розбити алгоритм на окремі частини, кожна з яких розв’язує свою самостійну підзадачу, і об’єднати ці підзадачі в єдине ціле.
Складання програми. Алгоритм має бути записаний мовою програмування. Процес розробки програми потребує доброго знання вибраної мови програмування і може здійснюватися теж за принципом «зверху донизу», що дозволяє одержати добре структуровану програму, читання і розуміння якої значно полегшене.
Компіляція програми. Переведення програми на машинну мову здійснюється за допомогою спеціальних програм — компіляторів. Однією з функцій компілятора є перевірка у програмі синтаксичних помилок і, за їх відсутності, побудова об’єктного модуля.
Компонування програми здійснюється компоновщиком (редактором зв’язків), який формує виконавчий модуль програми. На цьому етапі відбувається підключення бібліотек, з’єднання окремих модулів, тобто розв’язання зовнішніх посилань.
Налагодження програми. Окрім синтаксичних помилок, програма може мати помилки іншого типу — змістовні, ло гічні. Вони з’являються під час помилкового трактування умови поставленої задачі через недосконалість математичної моделі або недоліки у побудованому алгоритмі. Процес налагодження програми полягає в підготовці системи тестів, які містять набір вихідних даних, що мають відомий результат. Якщо для всіх тестів результати роботи програми збіглися з розрахунками, то можна вважати, що логічних помилок немає.
Експлуатація програми. Програма, що має відповідну документацію, може бути тиражована і запропонована іншим користувачам.
Поняття алгоритму
Алгоритм є фундаментальним поняттям інформатики. Відомий середньоазіатський мудрець, вчений, філософ і математик Мухаммед бен Муса аль-Хорезмі у IX ст. детально розробив правила чотирьох арифметичних дій (їх можна назвати алгоритмами арифметичних дій). При перекладі його наукових трактатів вперше з’явився термін «алгоритм» (аль-Хорезмі — Algorithmi).
Алгоритм — це наперед заданий чіткий опис скінченної послідовності вказівок, виконання яких дозволяє одержати правильний розв’язок задачі.
Алгоритм повинен відповідати певним вимогам і мати такі властивості:
- визначеність (детермінованість) — алгоритм має бути чітким і однозначним, кожна команда не повинна допускати довільності тлумачення, кожний крок алгоритму має бути точно визначеним;
- масовість — алгоритм повинен бути по можливості універсальним, розрахованим на розв’язання однотипних задач з різними вихідними даними;
- дискретність — визначений алгоритмом обчислювальний процес повинен мати дискретний (перервний) характер, тобто являти собою послідовність окремих завершених кроків — команд або дій;
- результативність — кожна дія має приводити до певного результату;
- формальність — будь-який виконавець, діючи за алгоритмом, може реалізувати поставлене завдання;
- скінченність — розв’язок задачі з використанням алгоритму має бути одержаним за скінченну кількість кроків.
Форми запису алгоритмів:
- Словесна форма: завдання описує алгоритм - інструкцію про вико- нання дій у певній послідовності за допомогою слів і пропозицій природної мови. Форма викладу довільна і встановлюється розробником.
- Формульно-словесна форма: інструкція про дії містить формальні си- мволи і вирази (формули) у поєднанні зі словесними поясненнями.
- Графічна форма або схема - це зображення алгоритму за допомогою геометричних фігур, які називаються блоками. Послідовність блоків і сполу- чних ліній утворюють схему.
- Псевдокод - система правил запису алгоритму з використанням набо- ру певних конструкцій для опису керуючих дій. Псевдокод дозволяє форма- льно зображати логіку алгоритму, використовуючи стандартизовані констру- кції природної мови для зображення управління та зберігаючи можливості мови для опису дій по обробці інформації.
- Мова програмування - це знакова система, призначена для опису про- цесів вирішення завдань та їх реалізації на ЕОМ. Реалізація означає, що опи- си можуть бути введені в ЕОМ і однозначно нею зрозумілі.
Запис алгоритмів здійснюється при їх розробці і поданні. Алгоритм являє собою певну інструкцію для виконавця, яку можна задати різними способами — словами, формулами, послідовністю обчислюваних операцій чи логічних дій тощо. На практиці застосовують різні способи запису алгоритмів у текстовій та графічній формі.
Пиклад словесного опису алгритму:
Розглянемо приклад алгоритму для знаходження середини відрізка за допомогою циркуля і лінійки.
Алгоритм розподілу відрізка АВ навпіл:
1) початок алгоритму;
2) поставити ніжку циркуля в точку А;
3) встановити розчин циркуля рівним довжині відрізка АВ;
4) провести коло;
5) поставити ніжку циркуля в точку В;
6) провести коло;
7) через точки перетину кіл провести пряму;
8) відзначити точку перетину цієї прямої з відрізком АВ.
9) кінець алгоритму
Велика кількість реальних завдань досить складна, тому між словесним описом дій і програмою на алгоритмічній мові виконується проміжний етап — побудова схеми алгоритму. Цей етап являє собою найбільш наочний спосіб зображення алгоритмів у вигляді графічних схем. Схема є нібито начерком структури програми та «путівником» за вже готовою програмою. При графічному способі зображення алгоритмів слід виконувати вимоги стандарту. В основі цього способу лежить поняття символу дії, який зображається окремою геометричною фігурою (таблиця 1).
Таблиця 1.

Під час створення схеми алгоритму блоки із записаними в них командами з’єднуються між собою стрілками для визначення черговості виконання дій алгоритму. Для запису команд всередині блоків використовується природна мова з елементами математичної символіки. Розробити алгоритм — це розбити задачу на етапи (більш прості задачі), що послідовно виконуються. При цьому чітко зазначаться як зміст кожного етапу, так і порядок їх виконання.
Основні типи алгоритмів — це три типові (базові) структури, які можна використовувати для розробки алгоритмів різного ступеня складності: лінійні, розгалуження та цикли.
Лінійним алгоритмом називається такий алгоритм, в якому лінійні команди виконуються послідовно одна за одною.
Розгалуженим алгоритмом називається алгоритм, що містить хоча б одну умову, в результаті перевірки якої здійснюється перехід до одного з можливих кроків. Процес розгалуження організується за допомогою логічного операторного блока.
Циклічний алгоритм містить повторення кілька разів з новими вихідними даними певної послідовності команд, що утворює тіло циклу. У циклі повинна існувати змінна (параметр циклу), яка при кожному наступному виконанні тіла циклу змінює своє значення і визначає кількість повторень.
Основні структури алгоритмів
У процесі розробки алгоритму рекомендується так званий структурний підхід, при якому використовуються лише три основні алгоритмічні структури – лінійний алгоритм, розгалужений і циклічний. Математично доведено, що будь-який алгоритм може бути представлений у вигляді комбінації цих основних структур. Особливість основних структур – кожна така структура має рівно один вхід і один вихід. Розглянемо основні структури алгоритмів.
3.1. Лінійний алгоритм
Найпростішим прикладом алгоритму є алгоритм лінійної структури. Він описує обчислювальний процес, у якому операції виконуються послідовно одна за одною.
Приклад лінійного алгоритму – алгоритм обчислення об’єму (V) прямокутного циліндра за задиними радіусом (r) основи і висотою (h). Алгоритм лінійної структури реалізується в такий спосіб (рисунок 1). Початок обробки даних – блок 1. Для проведення обчислень здійснюється введення в блоці 2 вихідних даних (значень r і h). У блоці 3 обчислюється об’єм циліндра V. Після обчислень здійснюється виведення результату (блок 4) і кінець (блок 5).

Рисунок 1.
Проте, розв’язання абсолютної більшості інженерних задач неможливопредставити лише за допомогою лінійних алгоритмів.
3.2. Алгоритми з розгалуженнями
Як правило, обчислювальний процес передбачає декілька можливих шляхів розв’язання задачі, реалізація яких залежить від виконання визначених умов. Алгоритм, що розгалужується, (або просто розгалуження) застосовується в тих випадках, коли в залежності від умови необхідно виконати одну або іншу групу дій. На рисунку 2 показано схему алгоритму, що розгалужується. Окремий випадок розгалуження – обхід, коли по гілці «ні» ніяких дій виконувати не треба (схема обходу – на малюнку 4.3).
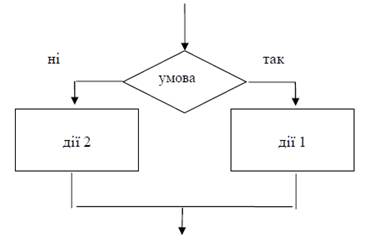
Рисунок 2.
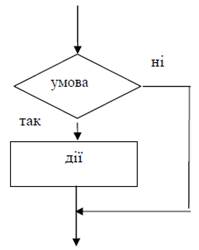
Рисунок 3.
Приклад. Обчислити значення f по одній із трьох формул – у залежності від значення x:

Схема алгоритму розвязання задачі наведена на рисунку 4.

Рисунок 4.
3.3. Циклічні алгоритми
Алгоритм, окремі дії в якому багаторазово повторюються, називається циклічним (або просто циклом).
Багаторазово повторювані дії алгоритму називаються тілом циклу. Очевидно, повторювати окремі обчислення доцільно при різних значеннях змінних. Одна з таких змінних називається керуючою змінною циклу. Значення керуючої змінної визначає, буде цикл продовжуватися або він буде завершений.
Перед виконанням циклу необхідно присвоїти початкові значення керуючій змінній циклу і тим змінним, які будуть обчислюватися в циклі. Цей етап називається підготовкою циклу. Потім необхідно перевірити умову продовження циклу і задати правило зміни керуючої змінної для повторного виконання циклу.
По числу повторень цикли поділяються на цикли з відомим числом повторень і цикли з невідомим числом повторень.
· Цикли з невідомим числом повторень
У циклах з невідомим числом повторень число повторень циклу заздалегідь не визначено, а обчислювальний процес завершується, якщо виконуватиметься деяка умова. Щоб підрахувати кількість повторень циклу, необхідно організувати лічильник, який треба знулити до початку циклу.
Цикли з невідомим числом повторень можуть бути двох типів – із передумовою (їх також називають циклами ПОКИ) і з постумовою (цикли ДО).
Схеми цих циклів показані на рисунку 5.

Рисунок 5.
Відмітимо, що умови, які перевіряються в цих циклах, взаємо протилежні: у циклі ПОКИ перевіряється умова продовження циклу, а в циклі ДО – умова виходу з циклу.
Особливість циклу ПОКИ: якщо при першій перевірці умова продовження порушується, те тіло циклу не буде виконано жодного разу.
Особливість циклу ДО: тіло циклу завжди виконується хоча б один раз.
В обчислювальному плані ці цикли еквівалентні, тобто в алгоритмі завжди можна замінити цикл ПОКИ циклом ДО і навпаки.
· Цикли з відомим числом повторень
Це цикли, у яких керуюча змінна змінюється у відомих межах по відомому закону. Найпростіший випадок – коли керуюча змінна i змінюється від свого початкового значення iн до кінцевого значення iк із кроком Δi. Трійка величин (iн, iк, Δі) називається параметрами циклу.
На рисунку 6 представлені різні варіанти організації такого циклічного процесу. Зліва – з постумовою; справа – з передумовою.

Рисунок 6.
На рисунку 7 наведено зображення циклу з використанням блоку – цикл. Він працює так само як і цикл з передумовою.

Рисунок 7.






