Определение. Функция y = F(x) называется бесконечно большой (б.б.) при x® a, если
.
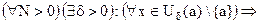
Это обозначается символом 
, хотя предел этой функций при 
не существует.
Пример. Функция 
является б.б. функцией при 
, так как
.
Очевидно, что любая б.б. функция не ограничена в окрестности точки 
.
Если 
и в некоторой окрестности точки а функция 
(соответственно 
), то еще пишут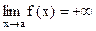 
(соответственно 
).
Отметим следующие свойства б.б. функций.
1) Сумма двух б.б. одного знака при является б.б. при .
2) Сумма б.б. функции при и ограниченной в окрестности точки а функции является б.б. при .
Пример. 
,так как х- есть б. б. при 
, а 
б. м., следовательно, ограниченная функция при 
.
3) Если 
б. б. при , а 
в некоторой окрестности точки а, то функция 
является б. б. при 
. В частности, произведение двух б. б. и произведение б. б. на функцию, имеющую ненулевой предел, является б. б.
Пример. 
, так как х – б.б. и 
.
4) Если 
б. б. при , то 
б.м. при .
5) Если 
б.м. при и 
при 
то 
является б.б. при .
Пример: 
, так как 
б. б. одного знака при 
.
3.3 Сравнение бесконечно малых и бесконечно больших
Определение. Бесконечно малая называется б.м. высшего порядка малости по сравнению с б.м. 
при в случае, если найдётся б.м. 
при такая, что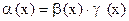 
. Соответствующее обозначение 
.
Пример: При 
, так как 
и 
есть б.м. при .
При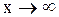 
: 
Определение. Бесконечно малые 
при называются эквивалентными, если 
. Обозначение 
~ 
. Подобное определение даётся и для б.б. функции.
Пример. Б.м. 
эквивалентны при , это следует из первого замечательного предела.
Это отношение эквивалентности удовлетворяет трём свойствам
1) ~ ;
2) ~ 
~ 
;
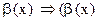3) Если ~ 
и 
~ 
, то ~ 
.
Теорема. Из ~ следует, что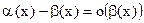 
.
Теорема. Пусть есть б. м. при , тогда:
1) 
;
2) 
~ ;
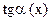3) 
~ ;
4) 
~ ;
5) 
~ ;
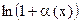6) 
~ 
, 
;
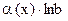7) 
~ 
.
Эти эквивалентные б.м. позволяют более просто вычислять некоторые пределы с помощью следующей теоремы.
Теорема. Пусть 
~ 
при , тогда
.
При этом оба записанных предела существуют одновременно. Если одно из выражений б. б., то другое также является б. б.
Пример. 
,
так как 
~ 
~ 
~ 
~ 
.
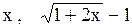Непрерывность функции
Определение. Функция 
называется непрерывной в точке 
, если выполняются три условия:
1) существует 
;
2) существует 
;
3) 
.
В символической форме это определение записывается так:
.
Функция называется непрерывной в точке 
слева (справа), если выполняются три условия:
1) 
;
2) 
.
Очевидно, что функция является непрерывной в точке в том и только в том случае, когда она непрерывна в этой точке слева и справа.
График непрерывной функции представляет из себя непрерывную линию.
Теорема (о непрерывности монотонной функции). Пусть функция монотонна (монотонно возрастает или монотонно убывает) на отрезке [а, 
] и принимает все значения из отрезка 
, тогда она непрерывна в каждой точке интервала (а, ), непрерывна в точке а справа и в точке 
слева. (рис.9)
 |
Рис. 9
Из этой теоремы следует, что все основные элементарные функции непрерывны во всех внутренних точках своей области определения, а во всех граничных точках области определения, принадлежащих ей, они непрерывны справа и слева. Это следует из того, что любую точку из области определения основной элементарной функции можно включить в отрезок, где эта функция монотонна и принимает все значения из отрезка 
.
Например, функция 
непрерывна во всех точках интервала
(–1,1), непрерывна в точке 
справа и в точке 
слева, так как оно монотонно возрастает в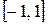 
и для
.
Теорема Пусть функции 
и 
непрерывны в точке . Тогда функции
1) 
, 2)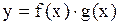 
, 3) при 
.
также непрерывны в точке .
Теорема (непрерывность сложной функции). Пусть функция непрерывна в точке и 
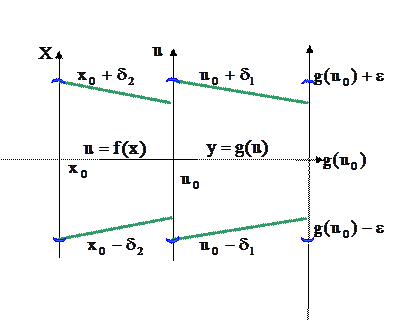, а функция 
непрерывна в точке 
. Тогда сложная функция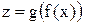 
непрерывна в точке .
Рис. 10
Следствие 1. Если 
и функция 
непрерывна в точке , то 
.
Пример. 
.
Следствие 2. Любая элементарная функция непрерывна во всех внутренних точках своей области определения, а в граничных точках отрезков области определения непрерывна справа или слева.
Это следует из теорем 1, 2, 3.
