Ограниченные величины и функции. Переменная величина  называется ограниченной, если существует такое число
называется ограниченной, если существует такое число  , что все значения
, что все значения  попадают в интервал
попадают в интервал  . Иными словами, для всех значений
. Иными словами, для всех значений  выполняется неравенство
выполняется неравенство
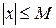
Для функции  ограниченность означает выполнение неравенства
ограниченность означает выполнение неравенства
 (*)
(*)
при всех  из области определения. Геометрически это условие означает, что все точки графика функции лежат в горизонтальной полосе между прямыми
из области определения. Геометрически это условие означает, что все точки графика функции лежат в горизонтальной полосе между прямыми 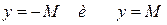 (рис. 7)
(рис. 7)
 y M
y M
 |
x

 |
-M
Рис. 7
Так, например, 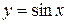 ограниченная функция, так как
ограниченная функция, так как  при всех
при всех  .
.
Иногда говорят об ограниченности функции лишь на некотором интервале, являющемся частью области определения; это значит, что условие (*) выполняется для рассматриваемого интервала; число  может зависеть от взятого интервала.
может зависеть от взятого интервала.
Пример.  - функция, не являющаяся ограниченной. В самом деле, какое бы
- функция, не являющаяся ограниченной. В самом деле, какое бы  мы не взяли, для тех
мы не взяли, для тех  , для которых
, для которых  будет выполняться неравенство
будет выполняться неравенство 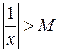 (рис.8).
(рис.8).
 y
y

x
0  x
x
Рис. 8
 В то же время на любом интервале
В то же время на любом интервале  эта функция ограничена:
эта функция ограничена:  (рис.9). Число
(рис.9). Число 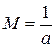 зависит от этого интервала.
зависит от этого интервала.
 y
y




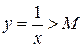

 M
M




 - x 0
- x 0


 x
x
 - M
- M





Рис. 9
Возрастание и убывание функций на интервале. Функция 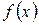 называется возрастающей на некотором интервале, если для любых двух значений аргумента, взятых на этом интервале, большему значению аргумента соответствует большее значение функции (рис.10).
называется возрастающей на некотором интервале, если для любых двух значений аргумента, взятых на этом интервале, большему значению аргумента соответствует большее значение функции (рис.10).
 |
y
 x1 x2
x1 x2  x
x
Рис.10
1. Функция 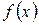 называется убывающей на некотором интервале, если для любых двух значений аргумента, взятых на этом интервале, большему значению аргумента соответствует меньшее значение функции (рис.11).
называется убывающей на некотором интервале, если для любых двух значений аргумента, взятых на этом интервале, большему значению аргумента соответствует меньшее значение функции (рис.11).
 y
y
0  x1 x2
x1 x2  x
x
Рис. 11
Запишем эти определения с помощью логических символов - кванторов: для интервала  - условие возрастания;
- условие возрастания;  - условие убывания.
- условие убывания.
Интервал, на котором функция возрастает или убывает, называется интервалом монотонности этой функции, а про функцию говорят, что она монотонна на этом интервале.
Пример 10.  (рис.12). Интервалы монотонности: на
(рис.12). Интервалы монотонности: на  функция убывает; на
функция убывает; на  функция возрастает.
функция возрастает.
 y
y
 |

 x
x
0
Рис.12
Четные и нечетные функции. Пусть задана функция  с областью определения
с областью определения 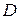 . Функция
. Функция  называется четной, если выполняется условие
называется четной, если выполняется условие
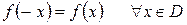
функция 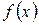 называется нечетной, если
называется нечетной, если

Примеры:
1. 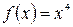 . Область определения
. Область определения 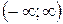 симметрична относительно начала координат
симметрична относительно начала координат  . Функция четная.
. Функция четная.
2. 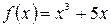 . Область определения
. Область определения 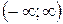 . Функция нечетная.
. Функция нечетная.
3.  . Область определения
. Область определения  (два интервала) симметрична относительно начала координат (множество всех действительных чисел с выброшенным нулем).
(два интервала) симметрична относительно начала координат (множество всех действительных чисел с выброшенным нулем).  . Функция нечетная.
. Функция нечетная.
4. Из тригонометрии известно, что 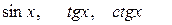 - нечетные функции;
- нечетные функции;  - четная функция.
- четная функция.
5. Геометрически четность функции означает, что ее график симметричен относительно оси ординат. Действительно, наряду с точкой  график содержит точку
график содержит точку  , так как
, так как  , точка
, точка 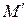 имеет координаты
имеет координаты  . Точки
. Точки  и
и 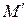 оказались симметричными относительно оси ординат (рис. 13).
оказались симметричными относительно оси ординат (рис. 13).
y


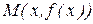
 |
x
 -x o x
-x o x
Рис. 13
Таким образом, наряду с произвольной точкой  график четной функции содержит и точку, симметричную ей относительно оси ординат, а значит, и весь график четной функции симметричен относительно оси
график четной функции содержит и точку, симметричную ей относительно оси ординат, а значит, и весь график четной функции симметричен относительно оси  (рис.14).
(рис.14).
 y
y
 |  | ||
Четная функция
 |
0 x

Рис. 14
 Рассуждая аналогичным образом, можно установить, что график нечетной функции симметричен относительно начала координат (рис.15).
Рассуждая аналогичным образом, можно установить, что график нечетной функции симметричен относительно начала координат (рис.15).
y 

0 x
 |
Рис. 15
Примеры:
1.  ; Пусть
; Пусть  и
и  , тогда,
, тогда,  т.е.
т.е.  и
и  . Значит, рассматриваемая функция не является ни четной, ни нечетной.
. Значит, рассматриваемая функция не является ни четной, ни нечетной.
2. 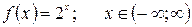 Пусть
Пусть  и
и  , тогда
, тогда 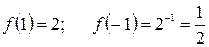 , т.е.
, т.е.  и
и  . Таким образом, эта функция является функцией общего вида.
. Таким образом, эта функция является функцией общего вида.
Период. Периодические функции. Число  называется периодом функции
называется периодом функции 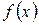 с областью определения
с областью определения 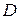 , если
, если

Функция 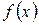 , обладающая периодом, называется периодической. Условие предполагает, конечно, что наряду с любым
, обладающая периодом, называется периодической. Условие предполагает, конечно, что наряду с любым 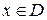 и
и 
Если число 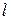 - период функции
- период функции 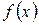 , то и любое целое, кратное
, то и любое целое, кратное 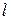 , т.е. число
, т.е. число  где
где 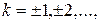 будет периодом
будет периодом 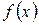 . Например,
. Например,  , т.е.
, т.е.  - период;
- период;  , т.е.
, т.е.  тоже период. В дальнейшем название периода функции будем применять к наименьшему положительному периоду.
тоже период. В дальнейшем название периода функции будем применять к наименьшему положительному периоду.
Пример. Из тригонометрии известно, что периоды функций  и
и  равны
равны  , а периоды
, а периоды  равны
равны  .
.
График периодической функции с периодом 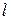 достаточно построить на
достаточно построить на
каком-либо интервале с длиной, равной периоду, а затем построенную часть графика сдвигать вдоль оси  на
на  и т. д. (рис. 16).
и т. д. (рис. 16).



 y
y
 |  |  |  |
 0 l x
0 l x
Рис.16
Пример. Периодична ли функция  (показательная)? Допустим, что периодична. Тогда
(показательная)? Допустим, что периодична. Тогда  , при этом для любого
, при этом для любого  ; отсюда
; отсюда  .
.
Это противоречит нашему предположению о существовании периода, значит, предположение неверно. Функция  не является периодической.
не является периодической.
1.3.1. Сложная функция (функция от функции). Пусть дана функция  от аргумента
от аргумента  , причем аргумент
, причем аргумент  , в свою очередь, является функцией от независимой переменной
, в свою очередь, является функцией от независимой переменной 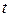 :
:

Возьмем какое-либо значение 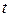 . В силу функциональной зависимости
. В силу функциональной зависимости  от
от 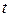 этому значению
этому значению 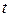 отвечает определенное значение
отвечает определенное значение  :
:  . Полученному значению
. Полученному значению  , в свою очередь, отвечает определенное значение
, в свою очередь, отвечает определенное значение

 ( рис.17 )
( рис.17 )
 y
y




x

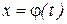
tt
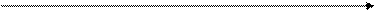 |
Рис.17
На рис. 17 переменные 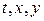 откладываются на трех осях, изображенных параллельно. В конечном итоге взятому значению
откладываются на трех осях, изображенных параллельно. В конечном итоге взятому значению 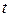 соответствует определенное значение
соответствует определенное значение  , т.е. переменная
, т.е. переменная  оказалась функцией независимой переменной
оказалась функцией независимой переменной 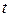 .
.
Получаем  . Функция
. Функция 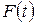 называется сложной функцией от независимой переменной
называется сложной функцией от независимой переменной 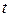 или функцией от функции (функция
или функцией от функции (функция  от функции
от функции  ). При этом функция
). При этом функция  называется заданной или внешней функцией, а
называется заданной или внешней функцией, а  - промежуточным аргументом. Функции
- промежуточным аргументом. Функции  и
и  называют еще составляющими для сложной функции
называют еще составляющими для сложной функции  ; говорят также, что
; говорят также, что  является суперпозицией функций
является суперпозицией функций  и
и  . Чтобы образовать функцию от функции, нужно, чтобы область значений промежуточной переменной
. Чтобы образовать функцию от функции, нужно, чтобы область значений промежуточной переменной  "укладывалась" в область определения заданной функции
"укладывалась" в область определения заданной функции  (рис.18). В противном случае среди значений функции
(рис.18). В противном случае среди значений функции  будут и такие, от которых значение функции
будут и такие, от которых значение функции 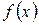 образовать нельзя (рис. 19). В таких случаях сложную функцию (или функцию от функции) можно задать только для тех значений независимой переменной
образовать нельзя (рис. 19). В таких случаях сложную функцию (или функцию от функции) можно задать только для тех значений независимой переменной 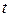 , для которых значения промежуточной переменной
, для которых значения промежуточной переменной  попадают в область определения внешней функции
попадают в область определения внешней функции  .
.


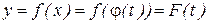 y
y
Область определения функции

x
Область значений функции 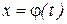
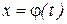
t
Область определения функции
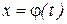 Рис.18
Рис.18
y
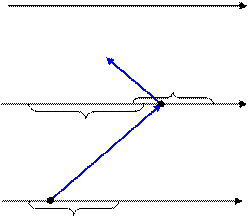
? Область значений функции
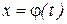
x
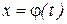
Область определения функции

t
Область определения функции
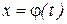
Рис.19
Примеры:
1. 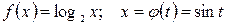 . Область значений промежуточной переменной
. Область значений промежуточной переменной 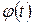 - отрезок [-1;1]; он не укладывается в область определения внешней функции
- отрезок [-1;1]; он не укладывается в область определения внешней функции  [ее область определения
[ее область определения  ]. Поэтому сложную функцию
]. Поэтому сложную функцию 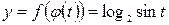 можно образовать только для тех значений аргумента
можно образовать только для тех значений аргумента 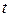 , для которых
, для которых  .
.
2.  . Здесь область значений промежуточного переменного
. Здесь область значений промежуточного переменного  , а область определения внешней функции
, а область определения внешней функции  . Значит, в этом случае образовать сложную функцию [т.е. суперпозицию функций
. Значит, в этом случае образовать сложную функцию [т.е. суперпозицию функций  и
и  ] нельзя.
] нельзя.
Сложные функции могут быть образованы и из большего числа составляющих.
Примеры:
1. у = x3; x = sint, t = 3w + l; у = F(w) = (sin(3w + l))3 - Здесь два промежуточных аргумента х и t, независимая переменная w.
2.  .
.
1.3.2. Обратная функция. Пусть на некотором интервале X задана функция  , область значений которой обозначим Y. Согласно определению функции каждому значению
, область значений которой обозначим Y. Согласно определению функции каждому значению  соответствует определенное значение
соответствует определенное значение 
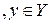 . Если же интервал X является интервалом монотонности для f(x), то и каждомузначению
. Если же интервал X является интервалом монотонности для f(x), то и каждомузначению  отвечает одно вполне определенное значение
отвечает одно вполне определенное значение  , для которого у = f(x) (рис.20). Таким образом, в этом случае функциональная зависимость между
, для которого у = f(x) (рис.20). Таким образом, в этом случае функциональная зависимость между  может рассматриваться и как функция
может рассматриваться и как функция  , т.е.
, т.е.  можно рассматривать как аргумент, а
можно рассматривать как аргумент, а  - как функцию. У функции
- как функцию. У функции  областью определения является Y, а областью значений - X. Функции
областью определения является Y, а областью значений - X. Функции  и
и  называются взаимно обратными
называются взаимно обратными  обратная функция к функции
обратная функция к функции  ;
;  - обратная функция к функции
- обратная функция к функции  . Уравнение
. Уравнение  получается в результате разрешения, если это возможно, уравнения
получается в результате разрешения, если это возможно, уравнения  относительно переменной
относительно переменной  .
.
Если f и  - взаимно обратные функции, то имеют место тождества (рис.21)
- взаимно обратные функции, то имеют место тождества (рис.21)

Графиком функции  является та же линия, которая изображала функцию y = f(x):ведь уравнение
является та же линия, которая изображала функцию y = f(x):ведь уравнение  - просто иначе переписанное уравнение у = f(x).
- просто иначе переписанное уравнение у = f(x).

Рис. 20 Рис. 21
Примеры:
1. 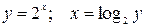 - обратная к ней функция. Областью определения функции у = 2х является
- обратная к ней функция. Областью определения функции у = 2х является  , этот же интервал является областью значений обратной функции
, этот же интервал является областью значений обратной функции  . Областью значений функции
. Областью значений функции  служит интервал
служит интервал  , он же является областью определения для
, он же является областью определения для  (рис.22). Обратная функция в этом примере существует потому, что
(рис.22). Обратная функция в этом примере существует потому, что  - возрастающая функция на всей числовой оси.
- возрастающая функция на всей числовой оси.
2.  (рис.17).
(рис.17).
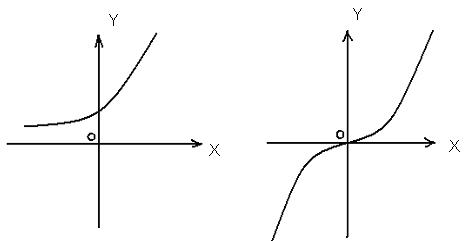
Рис.22 Рис.23
Функция  несколько неудобна тем, что, вопреки привычному, ее аргументом является
несколько неудобна тем, что, вопреки привычному, ее аргументом является  , а не
, а не  и значением функции служит
и значением функции служит  , а не
, а не  . Неудобство это скорее психологического характера, однако, чтобы его избежать, наряду с функцией
. Неудобство это скорее психологического характера, однако, чтобы его избежать, наряду с функцией  рассматривают функцию
рассматривают функцию  , которую также называют обратной функцией к функции
, которую также называют обратной функцией к функции  . Функция
. Функция  получается из
получается из  переменой ролей
переменой ролей  и
и  :
:
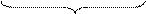


обратные функции к 
Примеры:
1. 

обратные функции к 
 2.
2. 
 |
обратные функции к 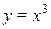
График обратной функции  симметричен графику функции
симметричен графику функции  относительно биссектрисы первого и третьего координатных углов.
относительно биссектрисы первого и третьего координатных углов.
При таком перегибании плоскости график нашей функции отобразится симметрично относительно биссектрисы первого и третьего координатных углов (рис.24). На рис.25 показаны графики взаимно обратных функций  и
и  .
.

Рис.24 Рис.25
1.3.3.Неявные функции. Иногда функциональная зависимость величин у и х задается некоторым уравнением, связывающим х и у, но нерешенным ни относительно у, ниотносительно х. Например, уравнение прямой  Правда, его очень просто решить относительно у:
Правда, его очень просто решить относительно у:  , и мы получаем обычное задание функции. Однако уравнение, связывающее х и у, не всегда удается разрешить относительно у или х. Таково, например, уравнение
, и мы получаем обычное задание функции. Однако уравнение, связывающее х и у, не всегда удается разрешить относительно у или х. Таково, например, уравнение  . Однако и здесь значениям х отвечают определенные значения у (например, значению х = 0 отвечает у = -2). В таких случаях говорят, что функция у - неявная функция от х, она задана уравнением, связывающим x и у. Подобным образом задаются многие кривые в аналитической геометрии. Например,
. Однако и здесь значениям х отвечают определенные значения у (например, значению х = 0 отвечает у = -2). В таких случаях говорят, что функция у - неявная функция от х, она задана уравнением, связывающим x и у. Подобным образом задаются многие кривые в аналитической геометрии. Например, 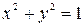 - уравнение окружности (с центром в начале координат и радиуса
- уравнение окружности (с центром в начале координат и радиуса  ). Здесь можно явно выразить у через х:
). Здесь можно явно выразить у через х:  , но получаются две функции, соответствующие "+" или "-" перед корнем (верхняя и нижняя полуокружности). Точно так же уравнение эллипса
, но получаются две функции, соответствующие "+" или "-" перед корнем (верхняя и нижняя полуокружности). Точно так же уравнение эллипса  заданием неявной функции. В самом общем виде уравнение, задающее неявную функцию, можно записать как
заданием неявной функции. В самом общем виде уравнение, задающее неявную функцию, можно записать как

где буква F "скрывает" те операции над х и у, которые следует проделать в основной (левой) части уравнения. Исследовать неявные функции почти всегда труднее.
1.3.4. Параметрическое задание функции. Кривые на плоскости часто задаются параметрическими уравнениями. В этих уравнениях координаты х и у точки на кривой выражены как функции третьего, вспомогательного переменного t (параметра):

Это новый, иногда наиболее удобный, способ задать функциональную зависимость между х и у. Считаем, что функция  имеет обратную:
имеет обратную:  . [т.е. решаем уравнение
. [т.е. решаем уравнение  относительно
относительно 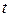 ]. Поставив это во второе уравнение, получим:
]. Поставив это во второе уравнение, получим:
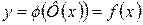
т.е. у есть функция от х (сложная функция).
Примеры:
1) 
2) 
параметрические уравнения: 1) окружности радиуса 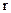 , 2) эллипса с полуосями а и b.
, 2) эллипса с полуосями а и b.
Весьма часто параметрическое задание линии возникает в механике. Там x и у - координаты движущейся точки, меняющиеся в зависимости от времени t, а линия - траектория этой точки.
Контрольные вопросы:
1. Дайте определение функции. Что называется областью определения функции?
2. Какая функция называется элементарной, сложной? Приведите примеры.
3. Четность, нечетность функция
4. Период и периодичность функции
5. Операции над множествами, их свойства
6. Область определения произведения и суммы функции
Литература:
Основная [2] Глава 1 § 1.1-1.11 стр. 9-31 Глава 2 § 2.1-2.12 стр. 34-64
Глава 3 § 3.1-3.2 стр. 66-85
[19] 2.1-2.4 стр. 138-162






