Переменная величина, характеризующая какой-то процесс, обычно возникает не индивидуально, а в связи с другими переменными величинами. Дело в том, что процессы, протекающие в окружающем мире, являются достаточно сложными и характеризуются многими переменными величинами, связи между которыми составляют закономерности, проявляющиеся в ходе данного процесса. Кроме того, любой процесс происходит не изолированно, а во взаимодействии с другими процессами.
Пример. Состояние газа при фиксированной температуре характеризуется давлением 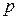 и объемом
и объемом 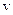 , занятым газом. Эти переменные величины связаны зависимостью
, занятым газом. Эти переменные величины связаны зависимостью 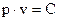 , где
, где  - постоянная (закон Бойля-Мариотта).
- постоянная (закон Бойля-Мариотта).
Математическую основу изучения связей между переменными величинами составляет понятие функциональной зависимости переменных величин или понятие функции.
Определение. Функцией f с областью определения D и областью значений Е называется некоторое отображение из D в Е, т. е. соответствие, при котором каждому элементу 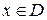 сопоставляется единственный элемент
сопоставляется единственный элемент 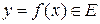 .
.
Буква  (или
(или  ) употребляется для обозначения функции чаще других, так как является пер-
) употребляется для обозначения функции чаще других, так как является пер-
вой буквой слова "funktion" - "функция". Иногда функции записываются и так:  ;
; 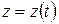 и т.д. При таких записях как бы "экономят" букву: и значение функции, и закон соответствия обозначают одной буквой. Понятие функции является основным понятием математического анализа. Что надо знать, чтобы была задана функция? Прежде всего, должна быть известна область значений аргумента
и т.д. При таких записях как бы "экономят" букву: и значение функции, и закон соответствия обозначают одной буквой. Понятие функции является основным понятием математического анализа. Что надо знать, чтобы была задана функция? Прежде всего, должна быть известна область значений аргумента  . Эта область значений аргумента называется областью определения функции. Затем мы должны знать, как по любому значению
. Эта область значений аргумента называется областью определения функции. Затем мы должны знать, как по любому значению  из области определения находится соответствующее ему значение
из области определения находится соответствующее ему значение
 . Правило
. Правило  , согласно которому по любому значению
, согласно которому по любому значению  из области определения находится соответствующее этому
из области определения находится соответствующее этому  значение
значение  , называется законом соответствия для данной функциональной зависимости.
, называется законом соответствия для данной функциональной зависимости.
Таким образом, для того чтобы функция была определена, надо знать: а) область определения; б) закон соответствия. Обычно функция задается аналитически - какой-нибудь формулой. Иногда закон соответствия задается разными формулами на разных участках ее области определения.
Примеры
1) Если D - множество всех студентов КазНТУ, а. Е - множество всех его институтов, то в качестве функции можно взять соответствие каждому студенту  института у, на котором он учится.
института у, на котором он учится.
2) Пусть D - множество всех векторов в пространстве, а  .
.
Функция  сопоставляет каждому вектору
сопоставляет каждому вектору 
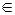 D его модуль у
D его модуль у 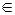 Е.
Е.
3) Площадь круга радиуса  :
: 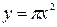 Область определения этой функции
Область определения этой функции 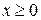 , т.е.
, т.е.  ; закон соответствия задан формулой
; закон соответствия задан формулой  .
.
4) 
Область определения этой функции - отрезок  ; закон соответствия задан разными формулами на разных участках:
; закон соответствия задан разными формулами на разных участках: 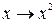 при
при 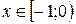 и
и  при
при 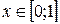 .
.
5)  . Область определения [0;4]. Область значений [0;2].
. Область определения [0;4]. Область значений [0;2].
Способы задания.
а) Табличный. Функция может быть задана в виде таблицы.
Например, пусть температуру Т воздуха измеряют через каждый час. Тогда каждому моменту времени t= 0,l,...,24 соответствует определенное число  (таблица 1):
(таблица 1):
Таблица 1
| t | ... | ||||
| Т | Т 
| T 
| Т 
| ... | T24 |
Таким образом, получена функция 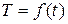 , определённая на множестве целых чисел от 0 до 24, заданная таблицей. Этот способ не даёт полной характеристики функции, поскольку в таблицу часто невозможно внести все точки из области определения функции.
, определённая на множестве целых чисел от 0 до 24, заданная таблицей. Этот способ не даёт полной характеристики функции, поскольку в таблицу часто невозможно внести все точки из области определения функции.
Например,
Таблица 2
| х | –1 | ||
| у |
соответствует и функции 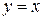 и
и 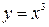 .
.
б) Графический. Графиком функции  называется множество точек (х,у) плоскости
называется множество точек (х,у) плоскости 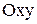 таких, что
таких, что 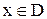 и
и 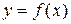 . График даёт наглядное представление о характере поведения функции.
. График даёт наглядное представление о характере поведения функции.
 Пусть задана функция
Пусть задана функция  . Возьмем на плоскости систему декартовых координат XOY. Рассмотрим множество
. Возьмем на плоскости систему декартовых координат XOY. Рассмотрим множество 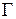 точек на плоскости
точек на плоскости  , абсциссами которых являются значения аргумента
, абсциссами которых являются значения аргумента  , а ординатами -соответствующие значения функции
, а ординатами -соответствующие значения функции 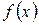 . Множество
. Множество 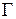 называется графиком функции
называется графиком функции 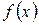 .
.
Y Г
 |
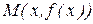
 0 x
0 x
Рис. 6
Построение графика функции дополняет аналитический {или какой-нибудь другой) способ задания функции, так как делает наглядным ход ее изменения. Во многих технических устройствах график функции возникает и как самостоятельный способ задания функции. Приборы вычерчивают график зависимости одной величины от другой (чаще всего от времени).
в) Аналитический. Аналитическим способом, т. е. с помощью одной формулы можно задавать только элементарные функции. Это самый универсальный способ задания функции, из которого можно получить и таблицу и график.




