Завдання 1.
Знайти невизначені інтеграли. У завданнях а), б), в), г) результати перевірити диференціюванням.
а)  .
.
Розв’язання. Нехай  , тоді
, тоді 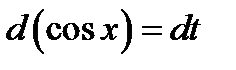 або
або  . Отже, маємо:
. Отже, маємо:

 .
.
Перевірка. 



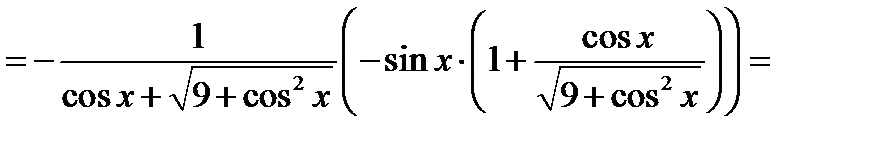
 .
.
Відповідь.  .
.
б)  .
.
Розв’язання. Оскільки  , то зробимо заміну
, то зробимо заміну  . Тоді
. Тоді  , і
, і
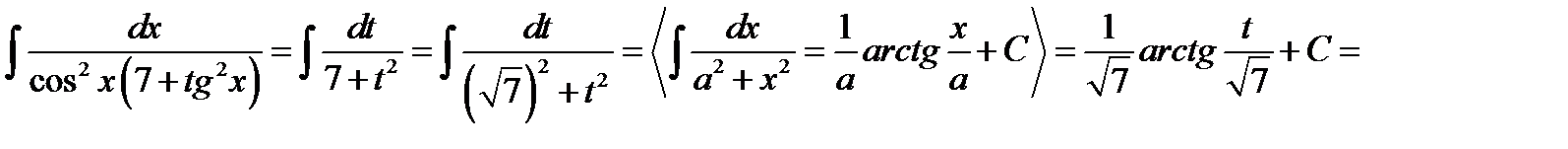
 .
.
Перевірка. 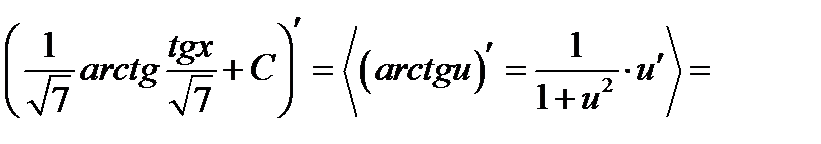
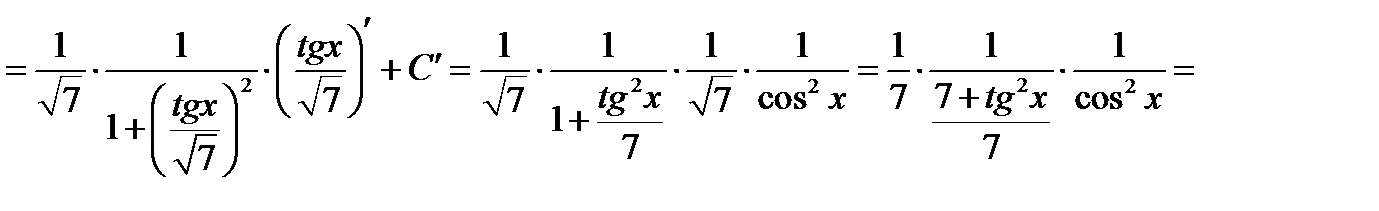
 .
.
Відповідь.  .
.
в)  .
.
Розв’язання. До заданого інтеграла застосуємо метод інтегрування частинами, скориставшись формулою  . Покладемо
. Покладемо  , а
, а  . Тоді
. Тоді  , а
, а  . За формулою інтегрування частинами маємо:
. За формулою інтегрування частинами маємо:


 .
.
Перевірка. 


 .
.
Відповідь. 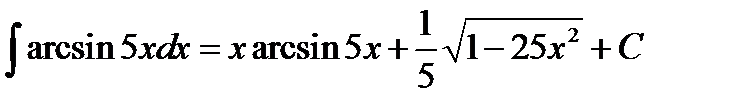 .
.
г)  .
.
Розв’язання. Підінтегральний раціональний дріб неправильний. Виділимо з нього цілу частину діленням чисельника на знаменник:
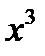
|

|

|

|

|

|

|

|

|

|
Маємо  . Розкладемо тепер дріб
. Розкладемо тепер дріб  на елементарні:
на елементарні:
1) знайдемо корені квадратного тричлена  :
:
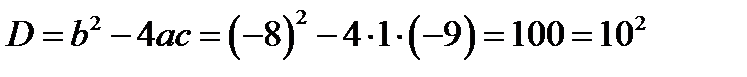 ;
;
 ;
;  ,
,  .
.
2) за формулою  маємо
маємо
 .
.
3)  . Знайдемо невизначені коефіцієнти
. Знайдемо невизначені коефіцієнти  і
і  :
: 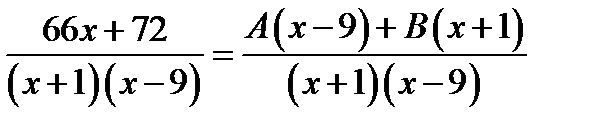 . З рівності дробів з однаковими знаменниками маємо
. З рівності дробів з однаковими знаменниками маємо  .
.
Якщо  , то
, то  ,
,  .
.
Якщо  , то
, то 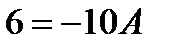 ,
,  .
.
Отже, 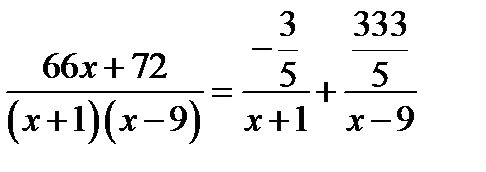 , а підінтегральний дріб матиме вигляд
, а підінтегральний дріб матиме вигляд  . Інтегруємо цей вираз
. Інтегруємо цей вираз

 .
.
Перевірка. 




 .
.
Відповідь.  .
.
д)  .
.
Розв’язання. Перетворимо підкореневий вираз:
 .
.
Нехай 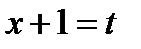 , тоді
, тоді  ,
, 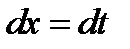 , і заданий інтеграл матиме вигляд:
, і заданий інтеграл матиме вигляд:

 . Обчислимо кожний із отриманих інтегралів окремо.
. Обчислимо кожний із отриманих інтегралів окремо.
 . Скористаємось формулою
. Скористаємось формулою  .
.
 .
.
 .
.
Таким чином,  , де
, де  .
.
Відповідь.  .
.
е)  .
.
Розв’язання. Перетворимо добуток тригонометричних функцій у суму за формулою 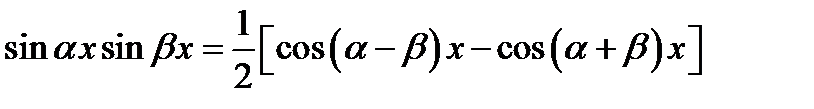 , а потім проінтегруємо одержаний вираз за відомими формулами з таблиці інтегралів і з використанням властивостей інтегралів:
, а потім проінтегруємо одержаний вираз за відомими формулами з таблиці інтегралів і з використанням властивостей інтегралів:

 .
.
Відповідь.  .
.
є)  .
.
Розв’язання. До поданого інтеграла застосуємо підстановку  . Тоді
. Тоді  , а
, а  ;
;  ,
,  . Одержимо
. Одержимо

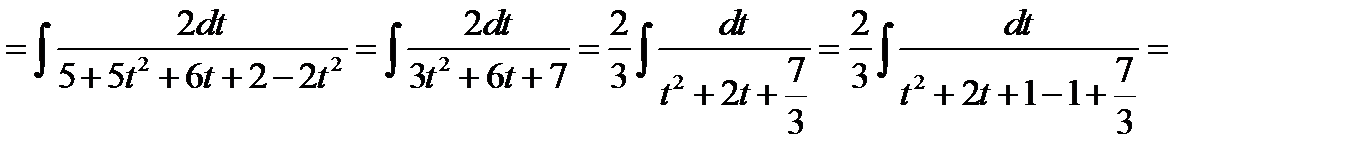
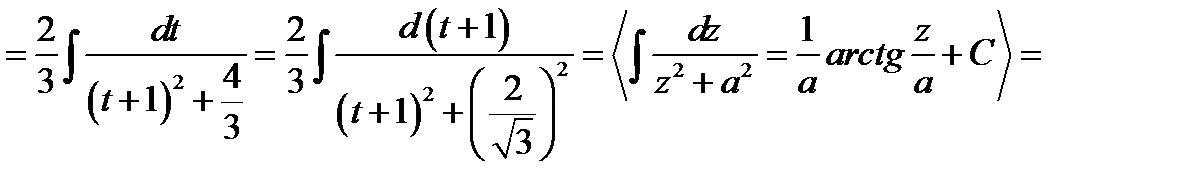
 .
.
Відповідь.  .
.
ж)  .
.
Розв’язання. Зведемо заданий інтеграл до інтеграла від раціональної функції за допомогою підстановки 
 . Тоді
. Тоді  , а
, а  . Дістанемо
. Дістанемо
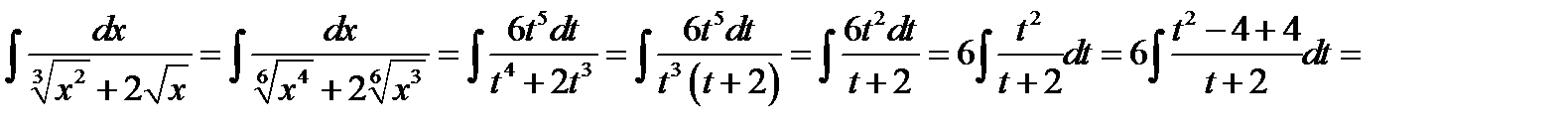

 .
.
Повертаючись до змінної 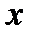 , одержуємо
, одержуємо
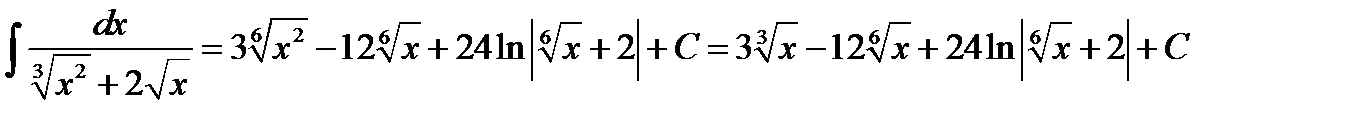 .
.
Відповідь.  .
.
Завдання 2.
Знайти площу фігури, обмеженої параболою  і прямою
і прямою  .
.
Розв’язання. Побудуємо фігуру, площу якої треба обчислити. Для цього знайдемо координати вершини параболи:
 ;
;  .
.
Таким чином,  .
.
Вісь 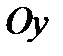 парабола перетинає в точці
парабола перетинає в точці  , а вісь
, а вісь 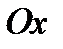 в точках
в точках  і
і 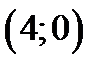 , координати яких знайдено з рівняння
, координати яких знайдено з рівняння  .
.

|
| -2 |
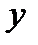
|

|
Координати точок перетину параболи і прямої знайдемо, розв’язавши систему рівнянь:
 ;
;  ;
;  ;
;  ;
;  .
.
Одержали  ,
,  . Абсциси цих точок є границями інтегрування при обчисленні площі побудованої фігури
. Абсциси цих точок є границями інтегрування при обчисленні площі побудованої фігури  . Таким чином,
. Таким чином,

 .
.
Відповідь.  .
.
Завдання 3.
Знайти об’єм тіла обертання відносно горизонтальної асимптоти для кривої  ,
,  .
.
Розв’язання. Для кривої  горизонтальною асимптотою є вісь
горизонтальною асимптотою є вісь  , оскільки
, оскільки  . Об’єм тіла, утвореного обертанням кривої
. Об’єм тіла, утвореного обертанням кривої  навколо осі
навколо осі  , обчислюється за формулою
, обчислюється за формулою
 ,
,
де за умовою задачі  ,
,  ,
,  . Отже, маємо
. Отже, маємо


 .
.
Відповідь. 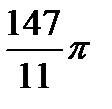 .
.
Завдання 4.
Знайти довжину дуги кривої  між точками її перетину з віссю
між точками її перетину з віссю  .
.
Розв’язання. Знайдемо абсциси точок перетину даної кривої з віссю  . Для цього розв’яжемо рівняння:
. Для цього розв’яжемо рівняння:
 :
:  ,
,  .
.
Довжину дуги кривої між точками з абсцисами  і
і  обчислимо за формулою
обчислимо за формулою 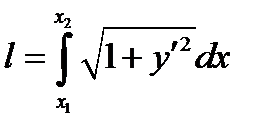 . Складемо вираз
. Складемо вираз  .
.

 .
.

 .
.
 . Знайдемо невизначений інтеграл
. Знайдемо невизначений інтеграл
 . Отже,
. Отже,  .
.
Відповідь.  .
.




